歡迎來到本博客️️️
作者研究:本科計算機專業,研究生電氣學碩。主要研究方向是電力系統和智能算法、機器學習和深度學習。目前熟悉python網頁爬蟲、機器學習、群智能算法、深度學習的相關內容。希望將計算機和電網有效結合!️️️
博主優勢:博客內容盡量做到思維缜密,邏輯清晰,為了方便讀者,博主專門做了一個專欄目錄,整個專欄只放了一篇文章,足見我對其重視程度:博主專欄目錄。做到極度細致,方便大家進行學習!親民!!!還有我開了一個專欄給女朋友的,很浪漫的喔,代碼學累的時候去瞧一瞧,看一看:女朋友的浪漫邂逅。有問題可以私密博主,博主看到會在第一時間回復。
目前更新:電力系統相關知識,期刊論文,算法,機器學習和人工智能學習。
支持:如果覺得博主的文章還不錯或者您用得到的話,可以免費的關注一下博主,如果三連收藏支持就更好啦!這就是給予我最大的支持!
歡迎您的到來
個人主頁:電力系統科研室
專欄目錄:電力系統與算法之美
【現在公眾號名字改為:荔枝科研社】
博主課外興趣:中西方哲學,送予讀者:
做科研,涉及到一個深在的思想系統,需要科研者邏輯缜密,踏實認真,但是不能只是努力,很多時候借力比努力更重要,然後還要有仰望星空的創新點和啟發點。當哲學課上老師問你什麼是科學,什麼是電的時候,不要覺得這些問題搞笑,哲學就是追究終極問題,尋找那些不言自明只有小孩子會問的但是你卻回答不出來的問題。在我這個專欄記錄我有空時的一些哲學思考和科研筆記:科研和哲思。建議讀者按目錄次序逐一浏覽,免得驟然跌入幽暗的迷宮找不到來時的路,它不足為你揭示全部問題的答案,但若能讓人胸中升起一朵朵疑雲,也未嘗不會釀成晚霞斑斓的別一番景致,萬一它居然給你帶來了一場精神世界的苦雨,那就借機洗刷一下原來存放在那兒的“真理”上的塵埃吧。
或許,雨過雲收,神馳的天地更清朗.......

本文目錄如下:️️️
目錄
1 概述
2 數學模型
2.1 目標函數
2.2 約束條件
3 運行結果
4 文章詳細講解及Python代碼
5 寫在最後
對於本文,我們選擇使用動態規劃,因為它看起來很適合解決這類問題,因為我們可以將問題分成階段。動態規劃是一種用於優化的方法,通過將問題劃分為多個子問題以構建最優解來計算最優解。動態規劃基於貝爾曼最優。也就是說,任何最優策略都由最優子策略組成,其中最優解的任何部分本身都是最優的。例如,在將城市 x 連接到城市 z 的最短路徑問題中,如果路徑通過城市 y,則 x 和 y 之間的路徑是最優的。動態規劃適用於幾個已知問題,例如背包問題、調度、最短路徑等。動態規劃算法將始終一個一個地解決子問題,並且要解決子問題,它將依賴於在前一個子問題中找到的解決方案。由於該系統,可以保證動態規劃算法找到的解決方案是最優的。
動態規劃通過每個子問題僅解決一次這一事實,可以降低空間和時間復雜性。在我們優化水電生產的案例中,渦輪機是一個子問題。實際上,使用從第一個渦輪機開始的簡單遞歸函數列出渦輪機問題的所有可能解決方案是很容易的,並且對於每個潛在的流量,將遞歸地嘗試每個其他渦輪機的所有流量。但是使用這種方法,我們會發現自己計算了每個渦輪機在一定流量下產生的功率的數倍。這就是為什麼在動態規劃中,我們會找到更有效的解決方案,因此將計算存儲在動態規劃表中,以便只執行一次。然後,當我們需要它們時,我們將在這些表中查找值。動態規劃包括兩個階段,前向階段(前向傳播)和後向階段(後向傳播)。
為了解決這個問題,我們首先看一下它的數學公式。原則是根據總流量(Qtot)和上游海拔最大化電力生產,我們將尋求最大化優化策略,因此我們將有:
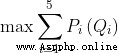
使用 Qi 分配給渦輪機 i 的流量。和 Pi 渦輪 i 的生產函數(見附錄 A )。那麼對於約束,我們只有最大總流量約束和最小流量限制:
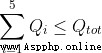
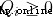
所以我們得到了最終的模型:
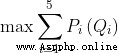
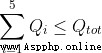
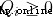
更詳細模型講解見第4部分。

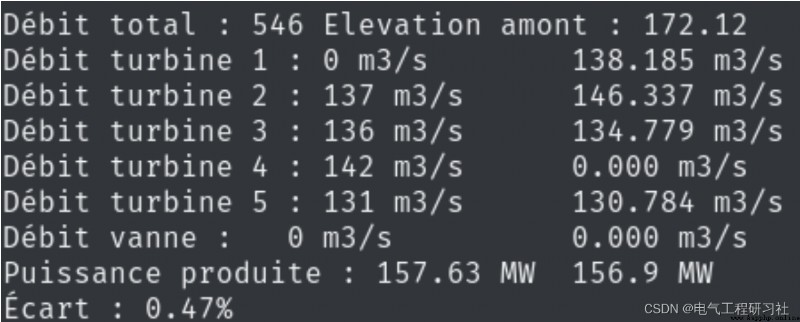
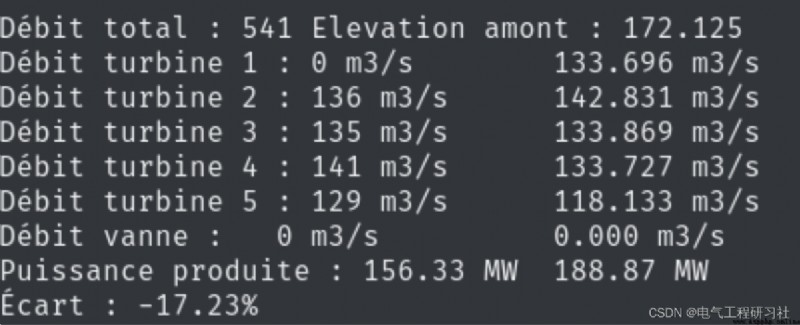
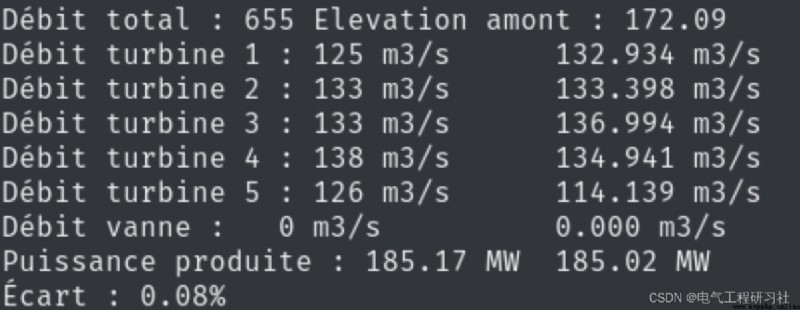
本文僅展現部分代碼,全部代碼見:正在為您運送作品詳情
部分理論引用網絡文獻,若有侵權請聯系博主刪除。