代碼位置:https://github.com/HappyBoy-cmd/fault_diagnosis_signal_processing
參考資料:
機械故障診斷及典型案例解析(第2版,時獻江)
隨機信號的幅值概率密度函數表示信號的幅值落在某一個指定區間內的概率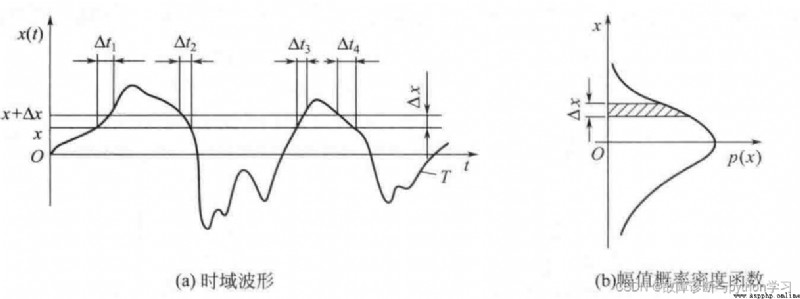
如上圖所示為時域波形及幅值概率密度。
x ( t ) x(t) x(t)值落在 x x x到 x + Δ x x+\Delta x x+Δx之間的時間為 T x = Δ t 1 + Δ t 2 + Δ t 3 + Δ t 4 T_{x}=\Delta t_{1}+\Delta t_{2}+\Delta t_{3}+\Delta t_{4} Tx=Δt1+Δt2+Δt3+Δt4,其總的觀測時間為 T T T,則出現的頻次可以用 T x / T T_{x} / T Tx/T;
當 Δ x \Delta x Δx趨於零時,就得到該點的幅值概率密度函數。
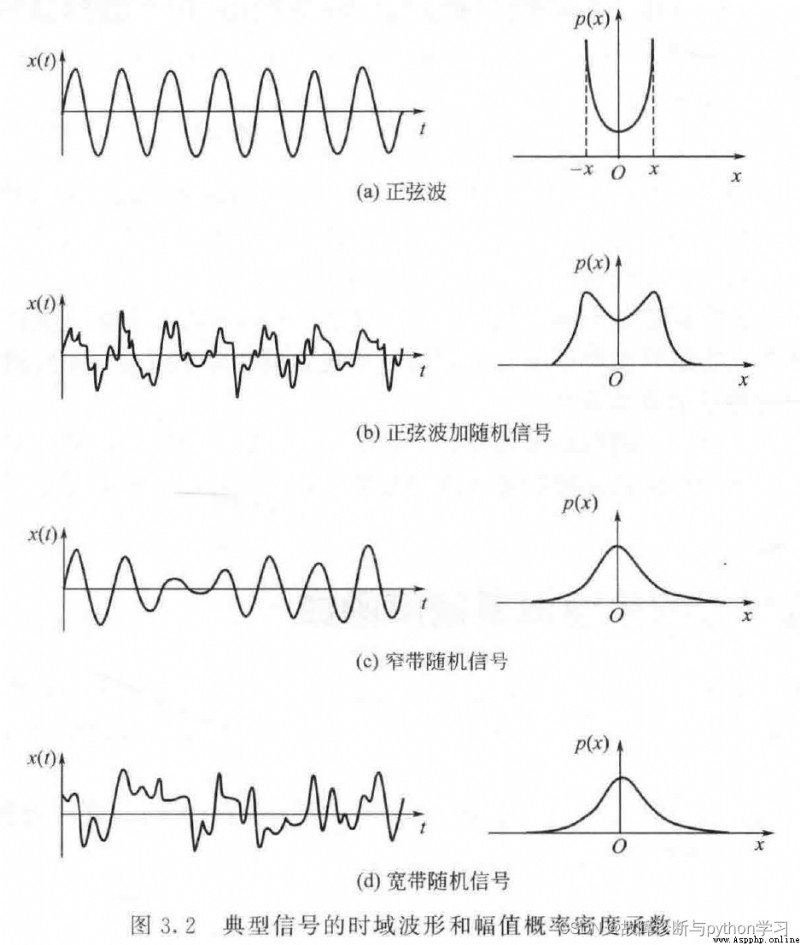
典型信號的時域波形和幅值概率密度函數如下圖所示,根據隨機過程理論,隨機信號的幅值概率密度函數符合正態分布規律;
確定性信號如簡諧信號的幅值概率密度函數則呈盆形曲線,如圖3.2(a)所示;
一般故障信號多是隨機信號和簡諧信號的混合體,所以當信號幅值概率密度函數的正態分布曲線上端出現盆型漏斗時[圖3. 2(b) ] ,往往預示著系統存在故障征兆。
import scipy.io as scio
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal, fftpack, stats
from matplotlib import rcParams
config = {
"font.family": 'serif', # 襯線字體
"font.size": 10, # 相當於小四大小
"font.serif": ['SimSun'], # 宋體
"mathtext.fontset": 'stix', # matplotlib渲染數學字體時使用的字體,和Times New Roman差別不大
'axes.unicode_minus': False # 處理負號,即-號
}
rcParams.update(config)
使用CWRU軸承數據進行分析,選取了4個mat文件,包括內圈故障、外圈故障、滾動體故障和正常狀態。
文件名解釋(以“1730_12k_0.007-InnerRace”為例):
1730:轉速,單位rpm
12k:采樣頻率,Hz
0.007:故障大小,單位inch,1inch=25.4mm
InnerRace:代表為內圈故障
def data_acquision(FilePath):
""" fun: 從cwru mat文件讀取加速度數據 param file_path: mat文件絕對路徑 return accl_data: 加速度數據,array類型 """
data = scio.loadmat(file_path) # 加載mat數據
data_key_list = list(data.keys()) # mat文件為字典類型,獲取字典所有的鍵並轉換為list類型
accl_key = data_key_list[3] # 獲取'X108_DE_time'
accl_data = data[accl_key].flatten() # 獲取'X108_DE_time'所對應的值,即為振動加速度信號,並將二維數組展成一維數組
return accl_data
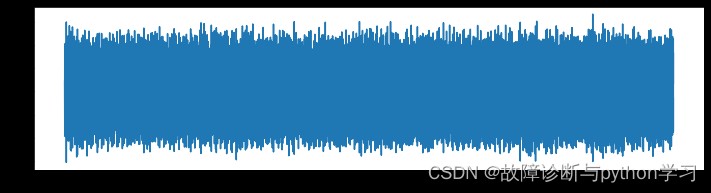
file_path = r'E:/研究生/pytorch/CSDN代碼/fault_diagnosis_signal_processing/第4篇-包絡譜/1730_12k_0.007-InnerRace.mat'
xt = data_acquision(file_path) #從mat文件獲取振動加速度數據
##--------繪制時域圖-------##
plt.figure(figsize=(12,3))
plt.plot(xt)
plt.show()
print(xt)
[ 0.22269856 0.09323776 -0.14651649 ... -0.36125573 0.31138814
0.17055689]
step1:確定幅值絕對值最大值max_value
step2:在幅值區間[-max_value, max_value]內等分劃分成n個小區間,區間長度為interval_len
step3:在幅值區間[-max_value, max_value]內等分劃分成n個小區間,每個區間長度為interval_len
step4:在第i個幅值小區間[-max_value+i * interval_len, max_value+(i+1) * interval_len]內,統計落入該區間的幅值個數count_num
step5:將n個區間統計的個數count_num形成一個列表count_num_list
step6:繪制柱狀圖,即得到幅值概率密度圖
def interval_num_count(data, low, high):
''' fun: 統計一維數據data落入某一個區間[low, high]內的數量 param low: 區間下限 param high: 區間上限 return count_num: 落入某一個區間[low, high]內的數量 '''
count_num = 0
for i in range(len(data)):
if data[i]>low and data[i]<high:
count_num += 1
return count_num
n = 10 # 分段數量
xt = xt - np.mean(xt) # 去直流分量(也叫零均值化處理)
max_value = np.abs( xt[np.argmax( np.abs(xt) )] ) # 確定幅值絕對值最大值max_value
count_num_list = []
for i in range(n):
interval_len = max_value*2/n # 在幅值區間[-max_value, max_value]內等分劃分成n個小區間,區間長度為interval_len
low = -max_value + i*interval_len # 第i個幅值小區間[-max_value+i * interval_len, max_value+(i+1) * interval_len]的下限
high = -max_value + (i+1)*interval_len # 第i個幅值小區間[-max_value+i * interval_len, max_value+(i+1) * interval_len]的上限
count_num = interval_num_count(data=xt, low=low, high=high) # 統計落入該區間的幅值個數count_num
count_num_list.append(count_num) # 將n個區間統計的個數count_num形成一個列表count_num_list
plt.bar(x=range( len(count_num_list) ), height=count_num_list) # 繪制柱狀圖,即得到幅值概率密度圖
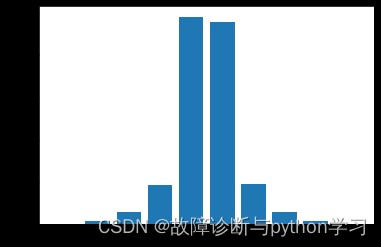
是不是已成雛形,有正態分布形狀了。只是原始區間分成了10份,看不太出來
下面分成100份
n = 100
xt = xt - np.mean(xt) # 去直流分量(也叫零均值化處理)
max_value = np.abs( xt[np.argmax( np.abs(xt) )] ) # 確定幅值絕對值最大值max_value
count_num_list = []
for i in range(n):
interval_len = max_value*2/n # 在幅值區間[-max_value, max_value]內等分劃分成n個小區間,區間長度為interval_len
low = -max_value + i*interval_len # 第i個幅值小區間[-max_value+i * interval_len, max_value+(i+1) * interval_len]的下限
high = -max_value + (i+1)*interval_len # 第i個幅值小區間[-max_value+i * interval_len, max_value+(i+1) * interval_len]的上限
count_num = interval_num_count(data=xt, low=low, high=high) # 統計落入該區間的幅值個數count_num
count_num_list.append(count_num) # 將n個區間統計的個數count_num形成一個列表count_num_list
plt.bar(x=range( len(count_num_list) ), height=count_num_list) # 繪制柱狀圖,即得到幅值概率密度圖
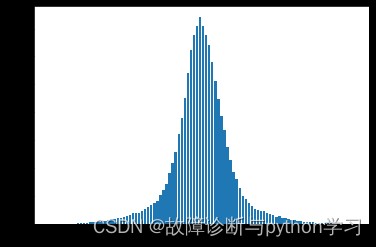
這下有正態分布那味了。不得不說這個形狀還挺優美的。
def plt_amp_prob_density_fun(data, n):
''' fun: 繪制幅值概率密度函數 param data: 輸入數據,1維array param n: 分割成段數的數量 return: 繪制幅值概率密度函數 '''
max_value = np.abs( xt[np.argmax( np.abs(xt) )] ) #
count_num = []
for i in range(n):
interval = max_value*2/n # 區間長度為interval_len
low = -max_value + i*interval # 區間下限
high = -max_value + (i+1)*interval # 區間上限
count = interval_num_count(data=xt, low=low, high=high) # 統計落入該區間的幅值個數
count_num.append(count)
plt.bar(x=range( len(count_num) ), height=count_num) # 繪制柱狀圖
plt.show()
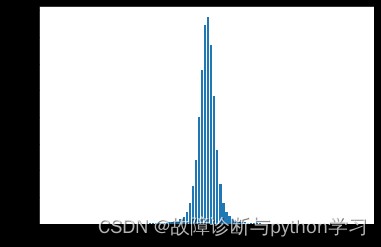
此時的正態分布形狀比較瘦小,峭度K大於3。K值大於3時,說明信號中沖擊成分幅值增大。
file_path = r'E:/研究生/pytorch/CSDN代碼/fault_diagnosis_signal_processing/第4篇-包絡譜/1730_12k_0.007-OuterRace3.mat'
xt = data_acquision(file_path)
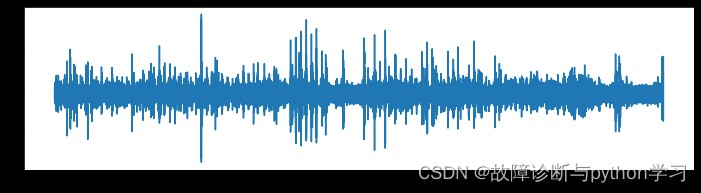
plt.figure(figsize=(12,3))
plt.plot(xt)
plt.show()
n = 100 # 設定分成份數
plt_amp_prob_density_fun(data=xt, n=n)
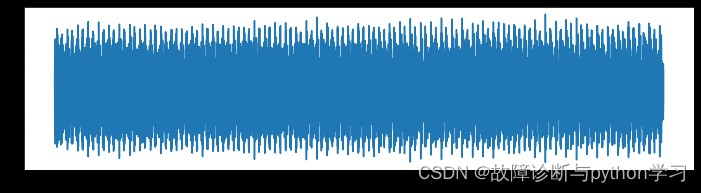
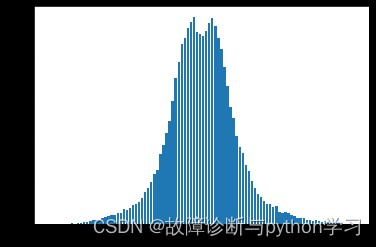
在頂部出現了第1節介紹時說的盆型漏斗
file_path = r'E:/研究生/pytorch/CSDN代碼/fault_diagnosis_signal_processing/第4篇-包絡譜/1730_48k_Normal.mat'
xt = data_acquision(file_path)
plt.figure(figsize=(12,3))
plt.plot(xt)
plt.show()
n = 100 # 設定分成份數
plt_amp_prob_density_fun(data=xt, n=n)
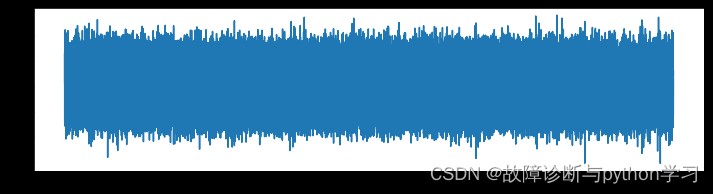
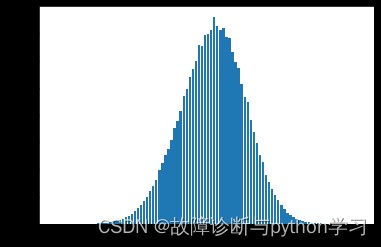
看著與標准正態分布挺像的
與正常狀態軸承的幅值概率密度函數相比,其故障軸承狀態有兩種情況