Dijkstra(迪傑斯特拉)算法是典型的單源最短路徑算法,用於計算一個節點到其他所有節點的最短路徑。主要特點是以起始點為中心向外層層擴展,直到擴展到終點為止。Dijkstra算法是很有代表性的最短路徑算法,在很多專業課程中都作為基本內容有詳細的介紹,如數據結構,圖論,運籌學等等。注意該算法要求圖中不存在負權邊。
問題描述:在無向圖 G=(V,E) 中,假設每條邊 E[i] 的長度為 w[i],找到由頂點 V0 到其余各點的最短路徑。(單源最短路徑)

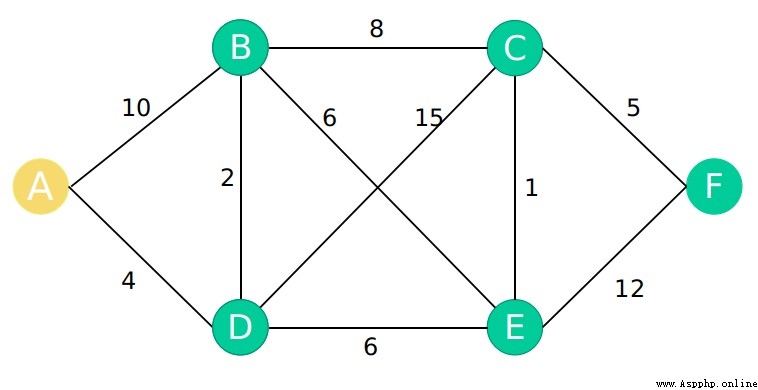
最後,我們得出
我們使得與節點有直接接觸的節點的距離為確定值,沒有直接接觸的節點為無窮大,然後構建一個二維矩陣
#!/usr/bin/env python
# -*- coding: UTF-8 -*-
__author__ = "A.L.Kun"
__file__ = "demo02.py"
__email__ = "[email protected]"
MAX = float('inf')
def dijkstra(matrix, start_node):
matrix_length = len(matrix) # 矩陣一維數組的長度,即節點的個數
used_node = [False] * matrix_length # 訪問過的節點數組
distance = [MAX] * matrix_length # 最短路徑距離數組
distance[start_node] = 0 # 初始化,將起始節點的最短路徑修改成0
# 將訪問節點中未訪問的個數作為循環值,其實也可以用個點長度代替。
while used_node.count(False):
min_value = MAX
min_value_index = -1
# 在最短路徑節點中找到最小值,已經訪問過的不在參與循環。
# 得到最小值下標,每循環一次肯定有一個最小值
for index in range(matrix_length):
if not used_node[index] and distance[index] < min_value:
min_value = distance[index]
min_value_index = index
# 將訪問節點數組對應的值修改成True,標志其已經訪問過了
used_node[min_value_index] = True
# 更新distance數組。
# 以B點為例:distance[x] 起始點達到B點的距離。
# distance[min_value_index] + matrix[min_value_index][index] 是起始點經過某點達到B點的距離,比較兩個值,取較小的那個。
for index in range(matrix_length):
distance[index] = min(distance[index], distance[min_value_index] + matrix[min_value_index][index])
return distance
matrix_ = [
[0,10,MAX,4,MAX,MAX],
[10,0,8,2,6,MAX],
[MAX,8,10,15,1,5],
[4,2,15,0,6,MAX],
[MAX,6,1,6,0,12],
[MAX,MAX,5,MAX,12,0]
]
ret = dijkstra(matrix_, 0)
print(ret)