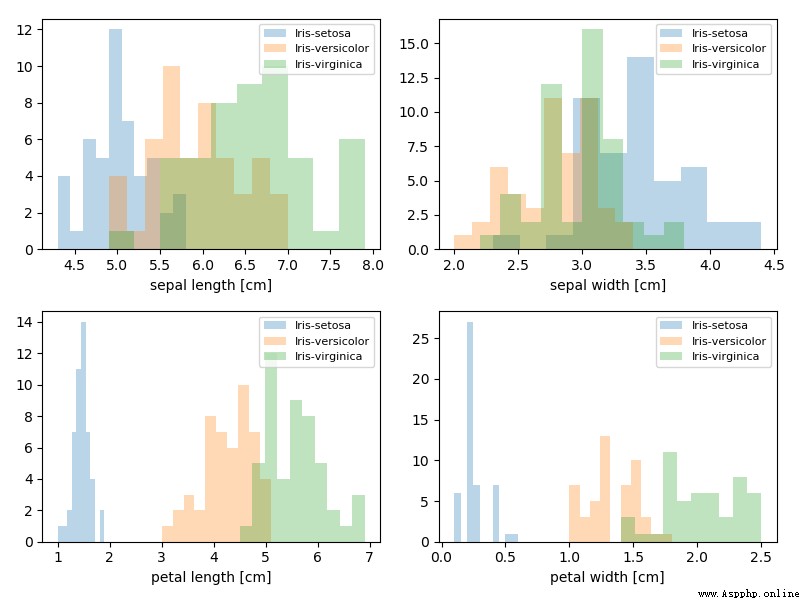
我們使用的是鸢尾花的數據集
python
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
import math
# 讀取數據源
df = pd.read_csv('E:/file/iris.data')
df.columns=['sepal_len', 'sepal_wid', 'petal_len', 'petal_wid', 'class']
print(df.head())
# 切分數據和標簽
X = df.iloc[:,0:4].values
y = df.iloc[:,4].values
label_dict = {
1: 'Iris-Setosa',
2: 'Iris-Versicolor',
3: 'Iris-Virgnica'}
feature_dict = {
0: 'sepal length [cm]',
1: 'sepal width [cm]',
2: 'petal length [cm]',
3: 'petal width [cm]'}
# 畫圖觀測數據集
plt.figure(figsize=(8, 6))
for cnt in range(4):
plt.subplot(2, 2, cnt+1)
for lab in ('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'):
plt.hist(X[y==lab, cnt],
label=lab,
bins=10,
alpha=0.3,)
plt.xlabel(feature_dict[cnt])
plt.legend(loc='upper right', fancybox=True, fontsize=8)
plt.tight_layout()
plt.show()
測試記錄:
sepal_len sepal_wid petal_len petal_wid class
0 4.9 3.0 1.4 0.2 Iris-setosa
1 4.7 3.2 1.3 0.2 Iris-setosa
2 4.6 3.1 1.5 0.2 Iris-setosa
3 5.0 3.6 1.4 0.2 Iris-setosa
4 5.4 3.9 1.7 0.4 Iris-setosa
代碼:
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
import math
from sklearn.preprocessing import StandardScaler
# 讀取數據源
df = pd.read_csv('E:/file/iris.data')
df.columns=['sepal_len', 'sepal_wid', 'petal_len', 'petal_wid', 'class']
#print(df.head())
# 切分數據和標簽
X = df.iloc[:,0:4].values
y = df.iloc[:,4].values
# 數據歸一化
X_std = StandardScaler().fit_transform(X)
# 協方差矩陣(對角線元素為1,自身與自身)
cov_mat = np.cov(X_std.T)
# 計算方陣的特征值和特征向量
eig_vals, eig_vecs = np.linalg.eig(cov_mat)
# 生成一個特征值和特征向量的二元組
eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:,i]) for i in range(len(eig_vals))]
#print(eig_pairs)
#print ('----------')
# 排序
eig_pairs.sort(key=lambda x: x[0], reverse=True)
# 輸出特征值:
print('Eigenvalues in descending order:')
for i in eig_pairs:
print(i[0])
# cumsum求累加值,然後乘100,就是百分比了
tot = sum(eig_vals)
var_exp = [(i / tot)*100 for i in sorted(eig_vals, reverse=True)]
print (var_exp)
cum_var_exp = np.cumsum(var_exp)
cum_var_exp
# 畫圖
plt.figure(figsize=(6, 4))
plt.bar(range(4), var_exp, alpha=0.5, align='center',
label='individual explained variance')
plt.step(range(4), cum_var_exp, where='mid',
label='cumulative explained variance')
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal components')
plt.legend(loc='best')
plt.tight_layout()
plt.show()
測試記錄:
Eigenvalues in descending order:
2.9244283691111135
0.9321523302535066
0.1494637348981336
0.02098259276427038
[72.6200333269203, 23.14740685864414, 3.7115155645845284, 0.5210442498510098]
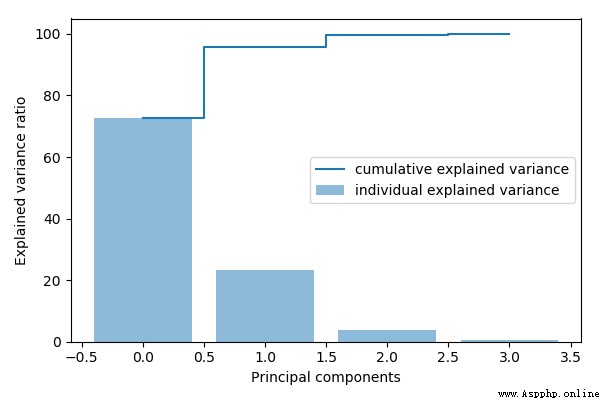
PCA降維的步驟:
代碼:
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
import math
from sklearn.preprocessing import StandardScaler
# 讀取數據源
df = pd.read_csv('E:/file/iris.data')
df.columns=['sepal_len', 'sepal_wid', 'petal_len', 'petal_wid', 'class']
#print(df.head())
# 切分數據和標簽
X = df.iloc[:,0:4].values
y = df.iloc[:,4].values
# 數據歸一化
X_std = StandardScaler().fit_transform(X)
# 協方差矩陣(對角線元素為1,自身與自身)
cov_mat = np.cov(X_std.T)
# 計算方陣的特征值和特征向量
eig_vals, eig_vecs = np.linalg.eig(cov_mat)
# 生成一個特征值和特征向量的二元組
eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:,i]) for i in range(len(eig_vals))]
#print(eig_pairs)
#print ('----------')
# 排序
eig_pairs.sort(key=lambda x: x[0], reverse=True)
# 根據特征值生成一個4*2矩陣
matrix_w = np.hstack((eig_pairs[0][1].reshape(4,1),
eig_pairs[1][1].reshape(4,1)))
# 原始矩陣 [15*4] * [4*2] = [15*2] 達到降維的效果
Y = X_std.dot(matrix_w)
# 降維前的效果
plt.figure(figsize=(6, 4))
for lab, col in zip(('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'),
('blue', 'red', 'green')):
plt.scatter(X[y==lab, 0],
X[y==lab, 1],
label=lab,
c=col)
plt.xlabel('sepal_len')
plt.ylabel('sepal_wid')
plt.legend(loc='best')
plt.tight_layout()
#plt.show()
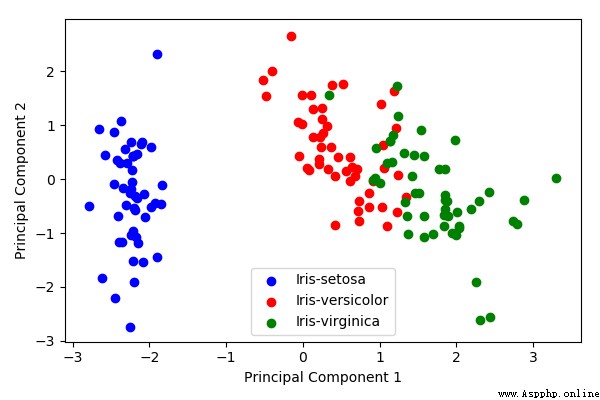
# 降維後的效果
plt.figure(figsize=(6, 4))
for lab, col in zip(('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'),
('blue', 'red', 'green')):
plt.scatter(Y[y==lab, 0],
Y[y==lab, 1],
label=lab,
c=col)
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.legend(loc='lower center')
plt.tight_layout()
plt.show()
測試記錄: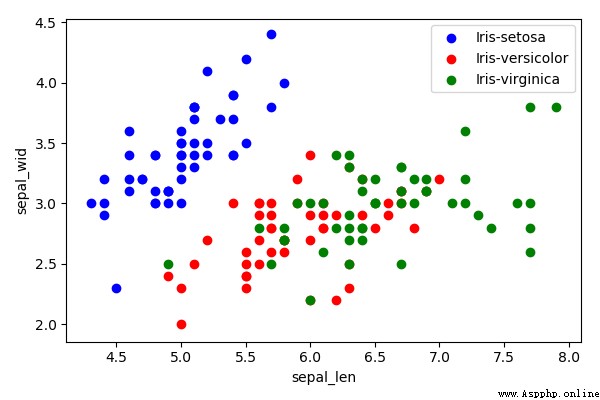
 Super simple to teach you how to clone sound in python (take Juan Fu as an example)
Super simple to teach you how to clone sound in python (take Juan Fu as an example)
Voice cloning is a popular dee
 I, the post-95 generation, with a monthly salary of 4K to 2w+, from the companys administrative chores to Python engineers, have made up my mind that things can be done
I, the post-95 generation, with a monthly salary of 4K to 2w+, from the companys administrative chores to Python engineers, have made up my mind that things can be done
I 95 after , Salary after one