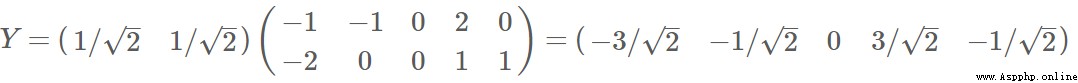PCA是Principal Component Analysis,主成分分析。
用途:
降維中最常用的一種手段
目標:
提取最有價值的信息(基於方差)
問題:
降維後的數據的意義?
內積: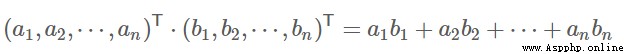
解釋:
設向量B的模為1,則A與B的內積值等於A向B所在
直線投影的矢量長度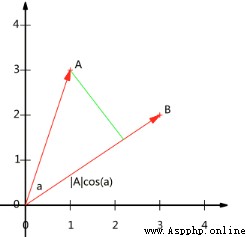
向量的表示:
向量可以表示為(3,2)
實際上表示線性組合: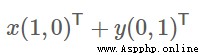
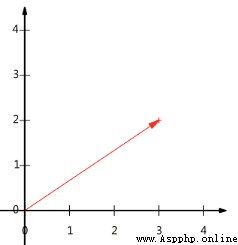
基:
(1,0)和(0,1)叫做二維空間中的一組基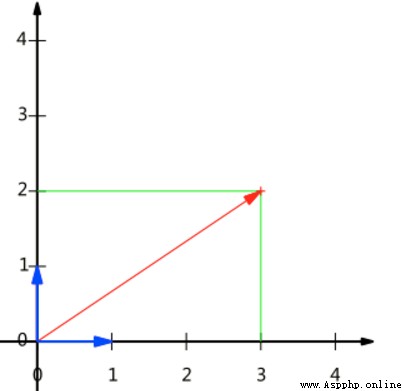
基是正交的(即內積為0,或直觀說相互垂直)
基是線性無關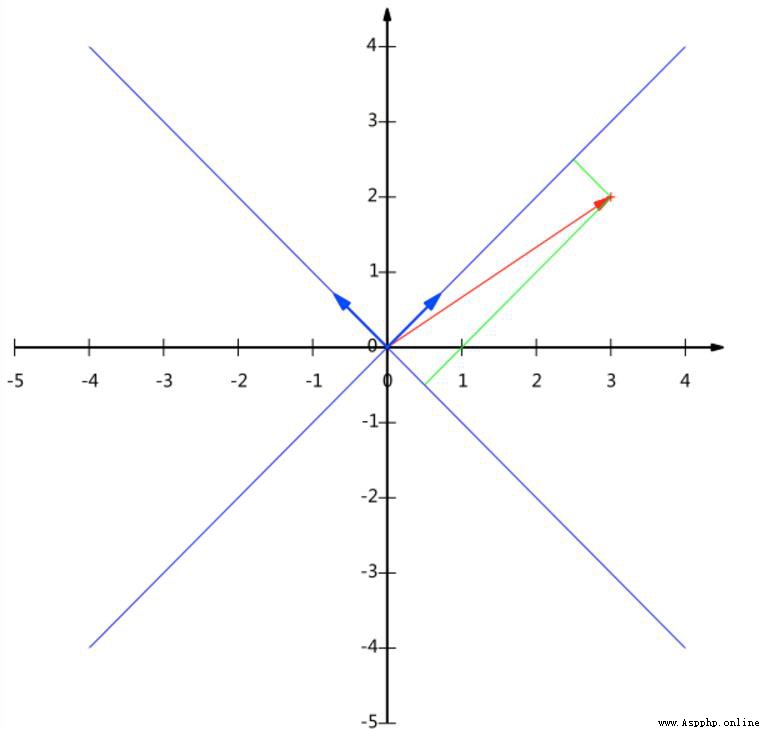
變換:
數據與一個基做內積運算,結果作為第一個新的坐標分量,然後與第二個基做內積運算,結果作為第二個新坐標的分量
數據(3,2)映射到基中坐標: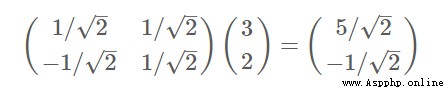
基變換: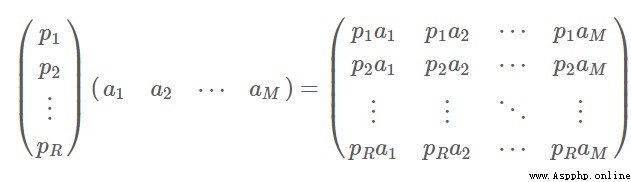
兩個矩陣相乘的意義是將右邊矩陣中的每一列列向量變換到
左邊矩陣中每一行行向量為基所表示的空間中去
方向:
如何選擇這個方向(或者說基)才能盡量保留最多的原始信息呢?一種直觀的看法是:希望投影後的投影值盡可能分散
方差: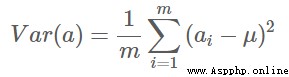
尋找一個一維基,使得所有數據變換為這個基上的坐標表示後,方差值最大
協方差(假設均值為0時):
如果單純只選擇方差最大的方向,後續方向應該會和方差最大的方向接近重合。
解決方案:
為了讓兩個字段盡可能表示更多的原始信息,我們是不希望它們之間存在(線性)相關性的
協方差:
可以用兩個字段的協方差表示其相關性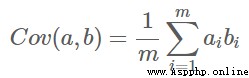
當協方差為0時,表示兩個字段完全獨立。為了讓協方差為0,選擇第二個基時只能在與第一個基正交的方向上選擇。因此最終選擇的兩個方向一定是正交的。
將一組N維向量降為K維(K大於0,小於N),目標是選擇K個單位正交基,使原始數據變換到這組基上後,各字段兩兩間協方差為0,字段的方差則盡可能大
協方差矩陣:
矩陣對角線上的兩個元素分別是兩個字段的方差,而其它元素是a和b的協方差。
協方差矩陣對角化:即除對角線外的其它元素化為0,並且在對角線上將元素按大小從上到下排列.
協方差矩陣對角化: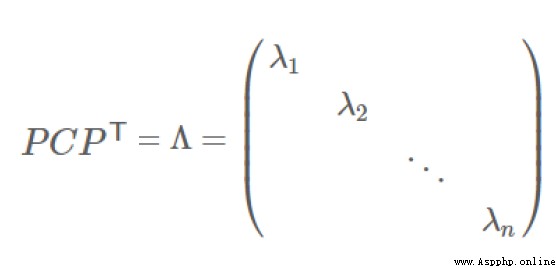
實對稱矩陣:
一個n行n列的實對稱矩陣一定可以找到n個單位正交特征向量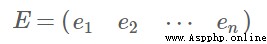
實對稱陣可進行對角化: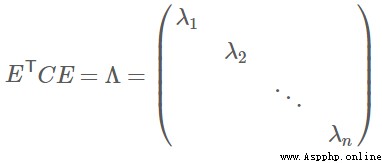
根據特征值的從大到小,將特征向量從上到下排列,則用前K行組成的矩陣乘以原始數據矩陣X,就得到了我們需要的降維後的數據矩陣Y
數據:
協方差矩陣: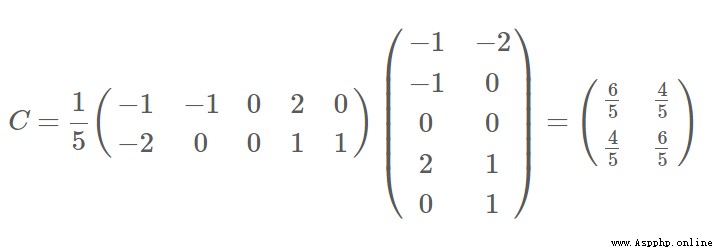
特征值: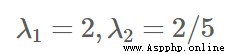
特征向量:
對角化: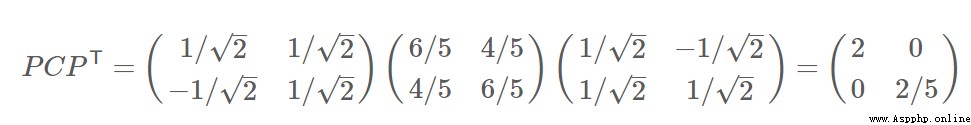
降維: