Be familiar with genetic algorithm .
Solve with genetic algorithm n queens problem .n*n On the chessboard n A queen , Two queens will attack each other if they are in the same straight line or the same diagonal . Find a way to swing , So that any two queens will not attack each other .
Problem description ： Examples of genetic algorithm ：8 queens problem
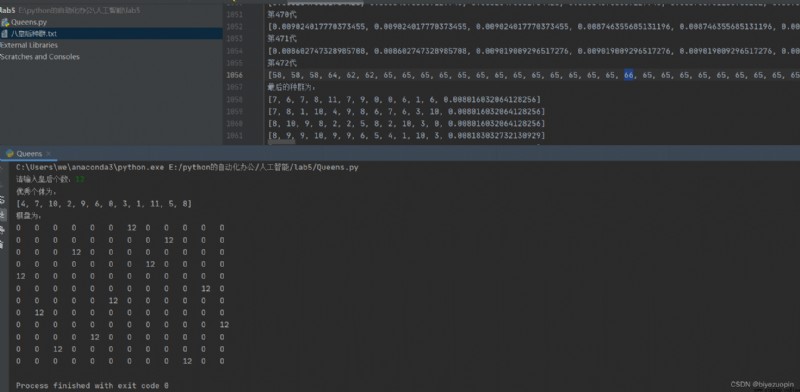
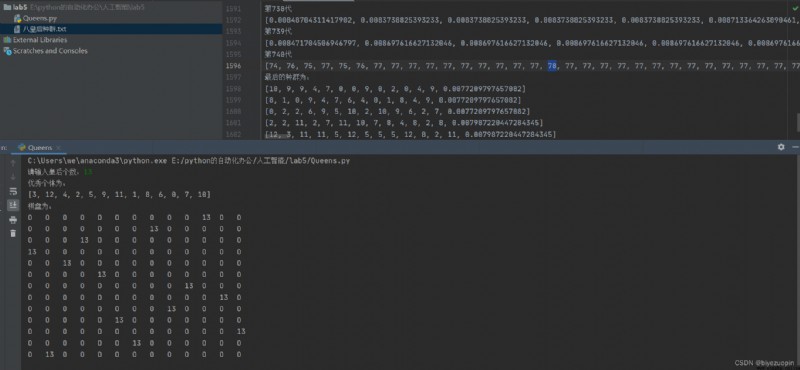
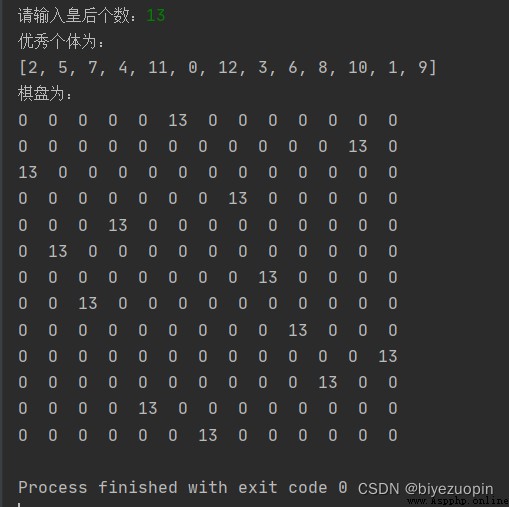
individual ： Long for 8 Sequence , The value of each column represents a pair The row of the queen who should be listed . Right picture status ：83742516
Fitness function = 28- The queen who attacked each other is right Number of ( The number of Queen pairs that do not attack each other )
A good state corresponds to a larger fitness function value (min = 0, max = 8 × 7/2 = 28.
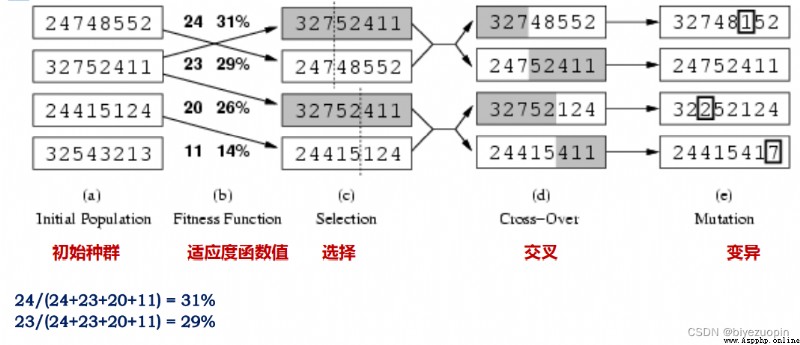
matters needing attention ：
The population size （ Number of individuals per generation ） Set up ： Try 20,50,100.
Iteration termination condition ： For the eight queens problem , The fitness function reaches 28（ Find the best solution ） Can be To terminate . There may also be a problem with your algorithm , As a result, the fitness function value can never be reached 28, So it's better to set a maximum number of iteration steps , Or when the fitness function value does not change Terminate the iteration when .
Cross rate ：0.5~1, Not too small .
Variation rate ：0.01~0.2, Only a few individuals are allowed to mutate , Not too big .
It is better for each generation to retain some individuals with high fitness function values in the previous generation to the next generation , So you Ensure that the results of the next generation are not worse than those of the previous generation .
Draw a simple picture of the final result 8 The queen placed the picture . Only in this way can we see whether there is conflict . Quite a Show a 8*8 Matrix , For example, the place where there is a queen displays numbers 8, Numbers are displayed elsewhere 0.
If it can be solved 8 queens problem , You can also try N queens problem （ for example N=32）.
The flow chart is as follows ：
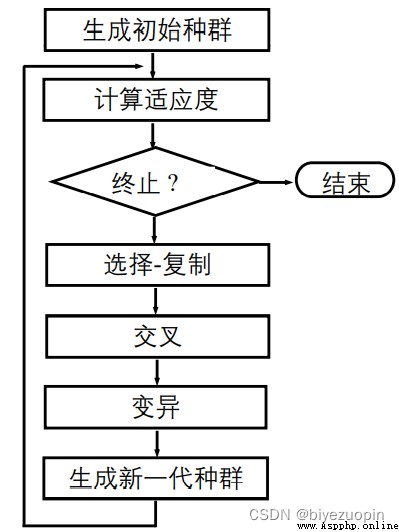
Experimental setup :
Initial population ： Enter the number of queens manually n, The size of the initialization population is a random number , The scope is 7n~13n Between , According to the number of queens, the size range of the population is different , The more queens there are, the larger the Group .
Fitness function ： Fitness function = n*（n-1)/2- The number of Queen pairs attacking each other ( The number of Queen pairs that do not attack each other ). Because of the problem, there is only one number in each column , So the columns do not conflict ; So just check whether the line and slash conflict . For Line top , Count the number of repetitions of each individual in the population , Judge whether the absolute value of the difference between the abscissa and the ordinate at a certain position is equal on the slash .
Eliminate ： Those with low fitness will eventually be eliminated . stay 0.13~0.145 Randomly generate a number between , Those with fitness less than this number will be eliminated , Later, it was found that this range did not apply to all species , If the population is small, fewer will be eliminated , Large populations will be eliminated , Sometimes, all individuals in the population are eliminated . Finally, add a field judgment in the later processing when the elimination rate is greater than 30% Adopt a new elimination mechanism —— All populations are sorted by fitness , The lower the fitness 25% Will be eliminated . In order to ensure that the size of the population is the same as the original , In the population that has not been eliminated, the same number of individuals are randomly selected for replication , Then disrupt the order .
Cross exchange ： Keep the individuals with high fitness to ensure that the results of the offspring are not worse than those of the parents , The ratio is 5%; Match all individuals with their corresponding fitness , Sort by fitness , Will rank first 5% Is retained to the next generation and deleted from the parent , Disorder the order of parents . Randomly generate half the size of the parent population , It indicates the position where two adjacent individuals of the parent cross and Exchange .
variation ： stay 0.01~0.04 A number is randomly generated as the rate of variation , You can get the number of mutated individuals Mutation_num, Random variation Mutation_num Variation position of individuals Mutationindexs, Randomly generated Mutation_num A sudden number , Put each of the offspring in Mutationindexs Mutation in the middle position
The experimental operation process and results are as follows ：
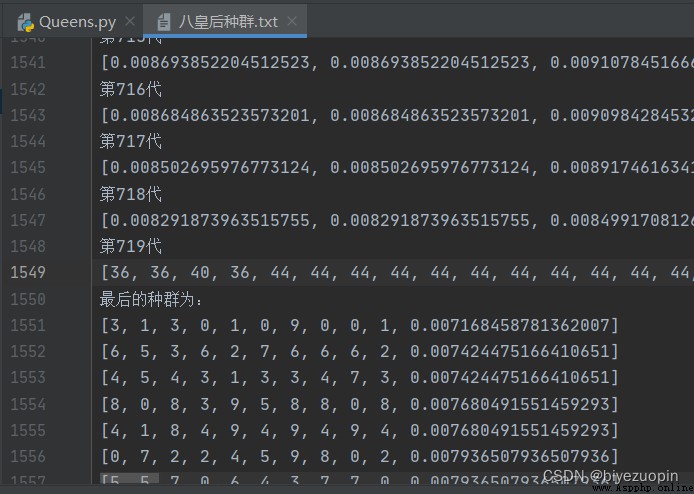
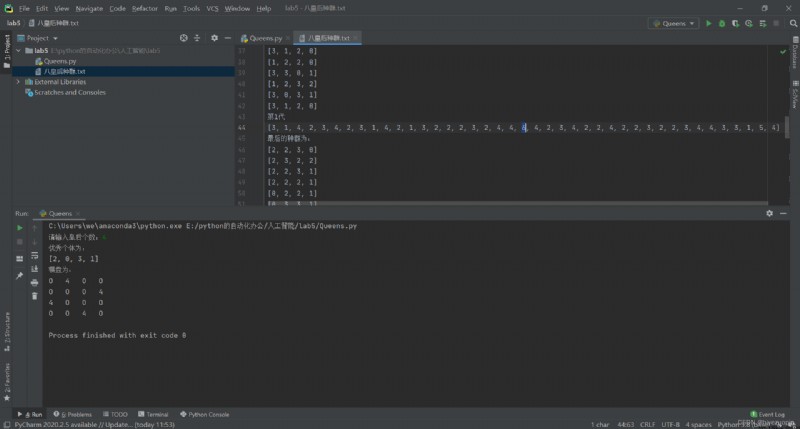
Queens don't fight each other ： And use text The file stores the initial population and the fitness of each individual in the iterative process . And the final population .
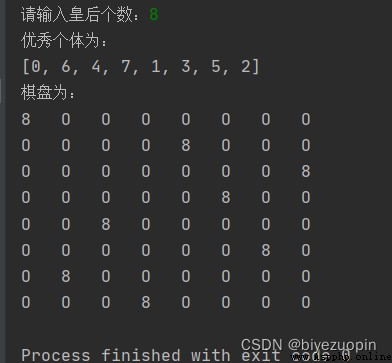
Queens don't fight each other ：
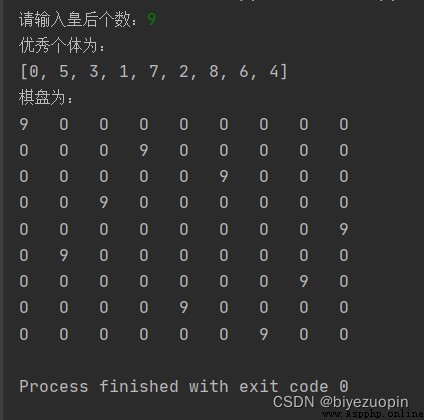
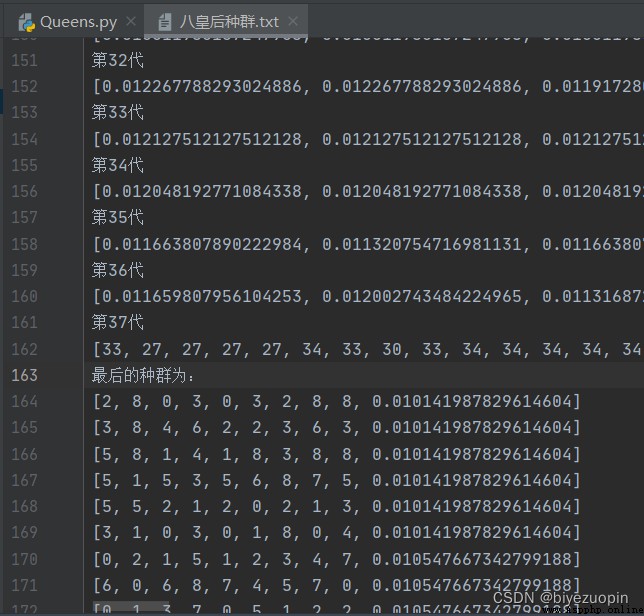
Queens don't fight each other ：
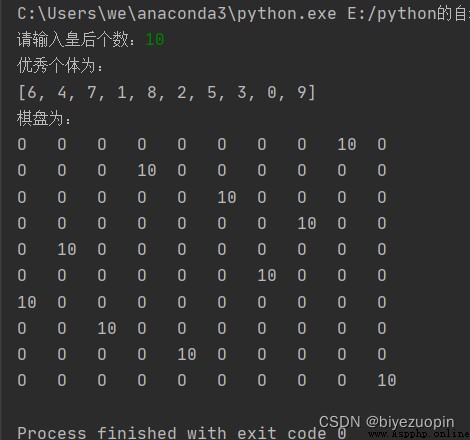
Queens don't fight each other ：
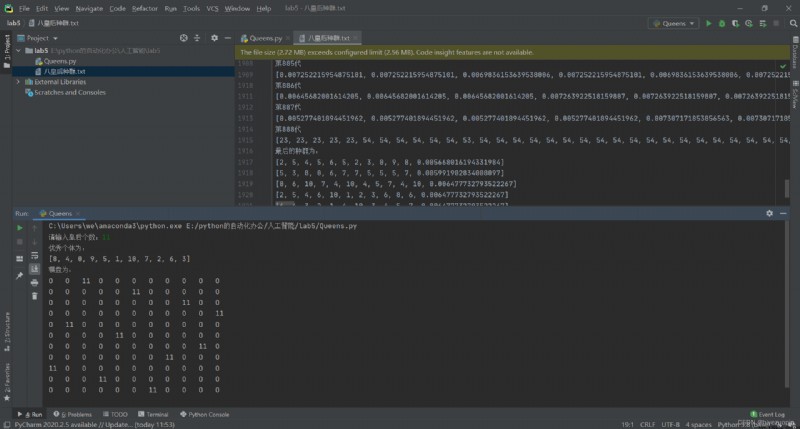
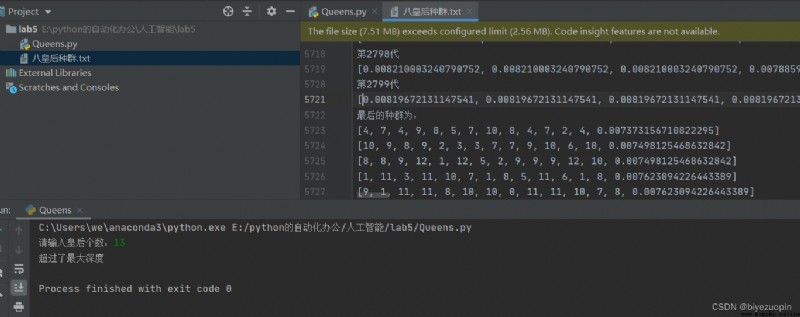
Queens don't fight each other ：
Queen
Exceeding the maximum depth
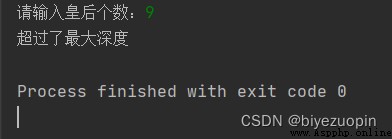
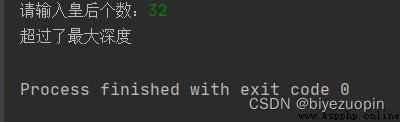
Queen ： The first generation succeeded , Make a note of
Python drawing square helix teenagers programming electronic society python programming level test level 2 real problem analysis September 2021
Catalog python Draw a square s
