手把手實現循環神經網絡

在此作業中，你將使用numpy實現你的第一個循環神經網絡。

循環神經網絡（RNN）在解決自然語言處理和其他序列任務上非常有效，因為它們具有“記憶”，可以一次讀取一個輸入 x < t > x^{<t>} x<t>（例如單詞），並通過從一個時間步傳遞到下一個時間步的隱藏層激活來記住一些信息/上下文。這使得單向RNN可以提取過去的信息以處理之後的輸入。雙向RNN則可以借鑒過去和未來的上下文信息。

符號：

• 上標 [ l ] [l] [l]表示與 l t h l^{th} lth層關聯的對象。
  • 例如： a [ 4 ] a^{[4]} a[4]是 4 t h 4^{th} 4th層激活。 W [ 5 ] W^{[5]} W[5]和 b [ 5 ] b^{[5]} b[5]是 5 t h 5{th} 5th層參數。
• 上標 ( i ) (i) (i)表示與 i t h i^{th} ith示例關聯的對象。
  • 示例： x ( i ) x^{(i)} x(i)是 i t h i^{th} ith訓練示例輸入。
• 上標 < t > {<t>} <t>表示在 t t h t^{th} tth時間步的對象。
  • 示例： x < t > x^{<t>} x<t>是在 t t h t^{th} tth時間步的輸入 x x x。 x ( i ) < t > x^{(i)<t>} x(i)<t>是示例 i i i的 t t h t^{th} tth時間步的輸入。
• 下標 i i i表示向量的 i t h i^{th} ith條目。
  • 示例： a i [ l ] a_i^{[l]} ai[l]​表示層 l l l中激活的 i t h i^{th} ith條目。

import numpy as np
import rnn_utils

1 循環神經網絡的正向傳播

在本周之後的作業，你將使用RNN生成音樂。你將實現的基本RNN具有以下結構。在此示例中， T x = T y T_x=T_y Tx​=Ty​。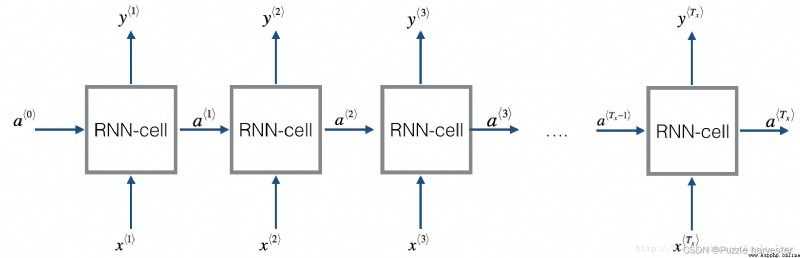

實現RNN的方法：

步驟：

1. 實現RNN的一個時間步所需的計算。
2. 在 T x T_x Tx​個時間步上實現循環，以便一次處理所有輸入。

1.1 RNN單元

循環神經網絡可以看作是單個cell的重復。你首先要在單個時間步上實現計算。下圖描述了RNN單元的單個時間步的操作。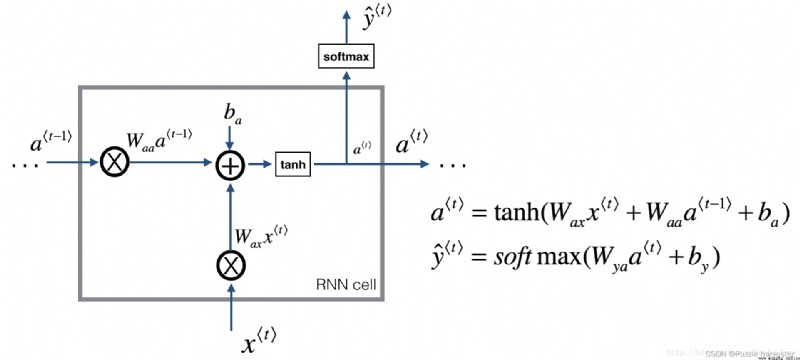

基礎RNN單元，將 x < t > x^{<t>} x<t>（當前輸入）和 a < t − 1 > a^{<t-1>} a<t−1>（包括過去信息的當前隱藏狀態）作為輸入，並輸出 a < t > a^{<t>} a<t>給下一個RNN單元，用於預測 y < t > y^{<t>} y<t>。

練習：實現上圖中描述的RNN單元。

說明：

1. 使用tanh激活計算隱藏狀態： a * t * = tanh ⁡ ( W a a a * t − 1 * + W a x x * t * + b a ) a^{\langle t \rangle} = \tanh(W_{aa} a^{\langle t-1 \rangle} + W_{ax} x^{\langle t \rangle} + b_a) a*t*=tanh(Waa​a*t−1*+Wax​x*t*+ba​)。
2. 使用新的隱藏狀態 a < t > a^{<t>} a<t>，計算預測 y ^ * t * = s o f t m a x ( W y a a * t * + b y ) \hat{y}^{\langle t \rangle} = softmax(W_{ya} a^{\langle t \rangle} + b_y) y^​*t*=softmax(Wya​a*t*+by​)。我們為你提供了一個函數：softmax。
3. 將 ( a * t * , a * t − 1 * , x * t * , p a r a m e t e r s ) (a^{\langle t \rangle}, a^{\langle t-1 \rangle}, x^{\langle t \rangle}, parameters) (a*t*,a*t−1*,x*t*,parameters)存儲在緩存中。
4. 返回 a * t * a^{\langle t \rangle} a*t* , y * t * y^{\langle t \rangle} y*t*並緩存。

我們將對 m m m個示例進行向量化處理。因此， x * t * x^{\langle t \rangle} x*t*維度將是 ( n x , m ) (n_x,m) (nx​,m)，而 a * t * a^{\langle t \rangle} a*t*維度將是 ( n a , m ) (n_a,m) (na​,m)。

def rnn_cell_forward(xt, a_prev, parameters):
""" 根據圖2實現RNN單元的單步前向傳播 參數： xt -- 時間步"t"輸入的數據，維度為(n_x, m) a_prev -- 時間步"t - 1"的隱藏狀態，維度為（n_a, m） parameters -- 字典，包含了以下內容: Wax -- 矩陣，輸入乘以權重，維度為（n_a, n_x） Waa -- 矩陣，隱藏狀態乘以權重，維度為（n_a, n_a） Wya -- 矩陣，隱藏狀態與輸出相關的權重矩陣，維度為（n_y, n_a） ba -- 偏置，維度為（n_a, 1） by -- 偏置，隱藏狀態與輸出相關的偏置，維度為（n_y, 1） 返回： a_next -- 下一個隱藏狀態，維度為（n_a， m） yt_pred -- 在時間步“t”的預測，維度為（n_y， m） cache -- 反向傳播需要的元組，包含了(a_next, a_prev, xt, parameters) """
# 從“parameters”獲取參數
Wax = parameters["Wax"]
Waa = parameters["Waa"]
Wya = parameters["Wya"]
ba = parameters["ba"]
by = parameters["by"]
# 使用上面的公式計算下一個激活值
a_next = np.tanh(np.dot(Waa, a_prev) + np.dot(Wax, xt) + ba)
# 使用上面的公式計算當前單元的輸出
yt_pred = rnn_utils.softmax(np.dot(Wya, a_next) + by)
# 保存反向傳播需要的值
cache = (a_next, a_prev, xt, parameters)
return a_next, yt_pred, cache

np.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
Waa = np.random.randn(5,5)
Wax = np.random.randn(5,3)
Wya = np.random.randn(2,5)
ba = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {
"Waa": Waa, "Wax": Wax, "Wya": Wya, "ba": ba, "by": by}
a_next, yt_pred, cache = rnn_cell_forward(xt, a_prev, parameters)
print("a_next[4] = ", a_next[4])
print("a_next.shape = ", a_next.shape)
print("yt_pred[1] =", yt_pred[1])
print("yt_pred.shape = ", yt_pred.shape)

a_next[4] = [ 0.59584544 0.18141802 0.61311866 0.99808218 0.85016201 0.99980978
-0.18887155 0.99815551 0.6531151 0.82872037]
a_next.shape = (5, 10)
yt_pred[1] = [0.9888161 0.01682021 0.21140899 0.36817467 0.98988387 0.88945212
0.36920224 0.9966312 0.9982559 0.17746526]
yt_pred.shape = (2, 10)

1.2 RNN正向傳播

你可以將RNN視為剛剛構建的單元的重復。如果輸入的數據序列經過10個時間步長，則將復制RNN單元10次。每個單元格都將前一個單元格( a * t − 1 * a^{\langle t-1 \rangle} a*t−1*)的隱藏狀態和當前時間步的輸入數據( x * t * x^{\langle t \rangle} x*t*)作為輸入，並為此時間步輸出隱藏狀態( a * t * a^{\langle t \rangle} a*t*)和預測( y * t * y^{\langle t \rangle} y*t*)。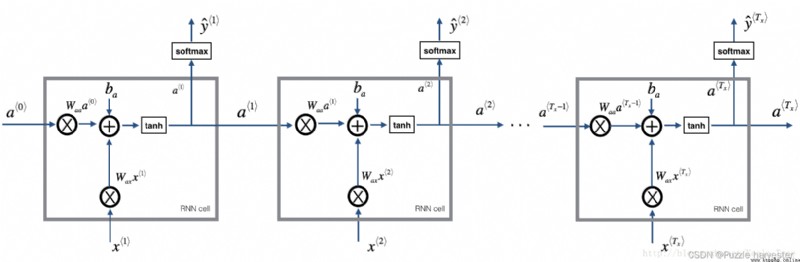

基本RNN。輸入序列 x = ( x * 1 * , x * 2 * , . . . , x * T x * ) x = (x^{\langle 1 \rangle}, x^{\langle 2 \rangle}, ..., x^{\langle T_x \rangle}) x=(x*1*,x*2*,...,x*Tx​*)執行 T x T_x Tx​個時間步。網絡輸出 y = ( y * 1 * , y * 2 * , . . . , y * T x * ) y = (y^{\langle 1 \rangle}, y^{\langle 2 \rangle}, ..., y^{\langle T_x \rangle}) y=(y*1*,y*2*,...,y*Tx​*)。

練習：編碼實現上圖中描述的RNN的正向傳播。

說明：

1. 創建一個零向量 ( a ) (a) (a)，該向量將存儲RNN計算的所有隱藏狀態。
2. 將“下一個”隱藏狀態初始化為 a 0 a_0 a0​（初始隱藏狀態）。
3. 開始遍歷每個時間步，增量索引為 t t t:
   • 通過運行rnn_step_forward更新“下一個”隱藏狀態和緩存。
   • 將“下一個”隱藏狀態存儲在 a a a中（ t t h t^{th} tth位置）
   • 將預測存儲在 y y y中
   • 將緩存添加到緩存列表中
4. 返回 a a a， y y y和緩存。

def rnn_forward(x, a0, parameters):
""" 根據圖3來實現循環神經網絡的前向傳播 參數： x -- 輸入的全部數據，維度為(n_x, m, T_x) a0 -- 初始化隱藏狀態，維度為 (n_a, m) parameters -- 字典，包含了以下內容: Wax -- 矩陣，輸入乘以權重，維度為（n_a, n_x） Waa -- 矩陣，隱藏狀態乘以權重，維度為（n_a, n_a） Wya -- 矩陣，隱藏狀態與輸出相關的權重矩陣，維度為（n_y, n_a） ba -- 偏置，維度為（n_a, 1） by -- 偏置，隱藏狀態與輸出相關的偏置，維度為（n_y, 1） 返回： a -- 所有時間步的隱藏狀態，維度為(n_a, m, T_x) y_pred -- 所有時間步的預測，維度為(n_y, m, T_x) caches -- 為反向傳播的保存的元組，維度為（【列表類型】cache, x)） """
# 初始化“caches”，它將以列表類型包含所有的cache
caches = []
# 獲取 x 與 Wya 的維度信息
n_x, m, T_x = x.shape
n_y, n_a = parameters["Wya"].shape
# 使用0來初始化“a” 與“y”
a = np.zeros([n_a, m, T_x])
y_pred = np.zeros([n_y, m, T_x])
# 初始化“next”
a_next = a0
# 遍歷所有時間步
for t in range(T_x):
## 1.使用rnn_cell_forward函數來更新“next”隱藏狀態與cache。
a_next, yt_pred, cache = rnn_cell_forward(x[:, :, t], a_next, parameters)
## 2.使用 a 來保存“next”隱藏狀態（第 t ）個位置。
a[:, :, t] = a_next
## 3.使用 y 來保存預測值。
y_pred[:, :, t] = yt_pred
## 4.把cache保存到“caches”列表中。
caches.append(cache)
# 保存反向傳播所需要的參數
caches = (caches, x)
return a, y_pred, caches

np.random.seed(1)
x = np.random.randn(3,10,4)
a0 = np.random.randn(5,10)
Waa = np.random.randn(5,5)
Wax = np.random.randn(5,3)
Wya = np.random.randn(2,5)
ba = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {
"Waa": Waa, "Wax": Wax, "Wya": Wya, "ba": ba, "by": by}
a, y_pred, caches = rnn_forward(x, a0, parameters)
print("a[4][1] = ", a[4][1])
print("a.shape = ", a.shape)
print("y_pred[1][3] =", y_pred[1][3])
print("y_pred.shape = ", y_pred.shape)
print("caches[1][1][3] =", caches[1][1][3])
print("len(caches) = ", len(caches))

a[4][1] = [-0.99999375 0.77911235 -0.99861469 -0.99833267]
a.shape = (5, 10, 4)
y_pred[1][3] = [0.79560373 0.86224861 0.11118257 0.81515947]
y_pred.shape = (2, 10, 4)
caches[1][1][3] = [-1.1425182 -0.34934272 -0.20889423 0.58662319]
len(caches) = 2

Nice！你已經從頭實現了循環神經網絡的正向傳播。對於某些應用來說，這已經足夠好，但是會遇到梯度消失的問題。因此，當每個輸出 y * t * y^{\langle t \rangle} y*t*主要使用"local"上下文進行估算時它表現最好（即來自輸入 x * t ′ * x^{\langle t' \rangle} x*t′*的信息，其中 t ′ t' t′是距離 t t t較近）。

在下一部分中，你將構建一個更復雜的LSTM模型，該模型更適合解決逐漸消失的梯度。LSTM將能夠更好地記住一條信息並將其保存許多個時間步。

2 長短期記憶網絡（LSTM）

下圖顯示了LSTM單元的運作。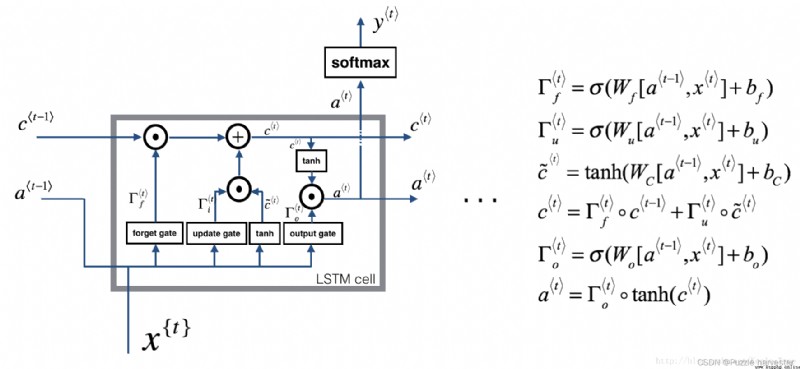

LSTM單元，這會在每個時間步上跟蹤並更新“單元狀態”或存儲的變量 c * t * c^{\langle t \rangle} c*t*，與 a * t * a^{\langle t \rangle} a*t*不同。

與上面的RNN示例類似，你將以單個時間步開始實現LSTM單元。然後，你可以從for循環內部迭代調用它，以使其具有 T x T_x Tx​時間步長的輸入。

2.0 關於“門”

遺忘門

為了便於說明，假設我們正在閱讀一段文本中的單詞，並希望使用LSTM跟蹤語法結構，例如主體是單數還是復數。如果主體從單數變為復數，我們需要找到一種方法來擺脫以前存儲的單/復數狀態的內存值。在LSTM中，遺忘門可以實現次數操作：
Γ f * t * = σ ( W f [ a * t − 1 * , x * t * ] + b f ) (1) \Gamma_f^{\langle t \rangle} = \sigma(W_f[a^{\langle t-1 \rangle}, x^{\langle t \rangle}] + b_f)\tag{1} Γf*t*​=σ(Wf​[a*t−1*,x*t*]+bf​)(1)
在這裡， W f W_f Wf​是控制遺忘門行為的權重。我們將 [ a * t − 1 * , x * t * ] [a^{\langle t-1 \rangle}, x^{\langle t \rangle}] [a*t−1*,x*t*]連接起來，然後乘以 W f W_f Wf​。上面的等式使得向量 Γ f * t * \Gamma_f^{\langle t \rangle} Γf*t*​的值介於0到1之間。該遺忘門向量將逐元素乘以先前的單元狀態 c * t − 1 * c^{\langle t-1 \rangle} c*t−1*。因此，如果 Γ f * t * \Gamma_f^{\langle t \rangle} Γf*t*​的其中一個值為0（或接近於0），則表示LSTM應該移除 c * t − 1 * c^{\langle t-1 \rangle} c*t−1*組件中的一部分信息（例如，單數主題），如果其中一個值為1，則它將保留信息。

更新門

一旦我們忘記了所討論的主體是單數，就需要找到一種更新它的方式，以反映新主體現在是復數。這是更新門的公式：
Γ u * t * = σ ( W u [ a * t − 1 * , x { t } ] + b u ) (2) \Gamma_u^{\langle t \rangle} = \sigma(W_u[a^{\langle t-1 \rangle}, x^{\{t\}}] + b_u)\tag{2} Γu*t*​=σ(Wu​[a*t−1*,x{ t}]+bu​)(2)
類似於遺忘門，在這裡 Γ u * t * \Gamma_u^{\langle t \rangle} Γu*t*​也是值為0到1之間的向量。這將與 c ~ * t * \tilde{c}^{\langle t \rangle} c~*t*逐元素相乘以計算 c * t * c^{\langle t \rangle} c*t*。

更新單元格

要更新新主體，我們需要創建一個新的數字向量，可以將其添加到先前的單元格狀態中。我們使用的等式是：
c ~ * t * = tanh ⁡ ( W c [ a * t − 1 * , x * t * ] + b c ) (3) \tilde{c}^{\langle t \rangle} = \tanh(W_c[a^{\langle t-1 \rangle}, x^{\langle t \rangle}] + b_c)\tag{3} c~*t*=tanh(Wc​[a*t−1*,x*t*]+bc​)(3)
最後，新的單元狀態為：
c * t * = Γ f * t * ∗ c * t − 1 * + Γ u * t * ∗ c ~ * t * (4) c^{\langle t \rangle} = \Gamma_f^{\langle t \rangle}* c^{\langle t-1 \rangle} + \Gamma_u^{\langle t \rangle} *\tilde{c}^{\langle t \rangle} \tag{4} c*t*=Γf*t*​∗c*t−1*+Γu*t*​∗c~*t*(4)

輸出門

為了確定我們將使用哪些輸出，我們將使用以下兩個公式：
Γ o * t * = σ ( W o [ a * t − 1 * , x * t * ] + b o ) (5) \Gamma_o^{\langle t \rangle}= \sigma(W_o[a^{\langle t-1 \rangle}, x^{\langle t \rangle}] + b_o)\tag{5} Γo*t*​=σ(Wo​[a*t−1*,x*t*]+bo​)(5)
a * t * = Γ o * t * ∗ tanh ⁡ ( c * t * ) (6) a^{\langle t \rangle} = \Gamma_o^{\langle t \rangle}* \tanh(c^{\langle t \rangle})\tag{6} a*t*=Γo*t*​∗tanh(c*t*)(6)
在等式5中，你決定使用sigmoid函數輸出；在等式6中，將其乘以先前狀態的tanh。

2.1 LSTM單元

練習：實現上圖中描述的LSTM單元。

說明：

1. 將 a * t − 1 * a^{\langle t-1 \rangle} a*t−1*和 x * t * x^{\langle t \rangle} x*t*連接在一個矩陣中： c o n c a t = [ a * t − 1 * x * t * ] concat = \begin{bmatrix} a^{\langle t-1 \rangle} \\ x^{\langle t \rangle} \end{bmatrix} concat=[a*t−1*x*t*​]
2. 計算公式1 - 6，你可以使用sigmoid()和np.tanh()。
3. 計算預測 y * t * y^{\langle t \rangle} y*t*，你可以使用sigmoid()。

def lstm_cell_forward(xt, a_prev, c_prev, parameters):
""" 根據圖4實現一個LSTM單元的前向傳播。 參數： xt -- 在時間步“t”輸入的數據，維度為(n_x, m) a_prev -- 上一個時間步“t-1”的隱藏狀態，維度為(n_a, m) c_prev -- 上一個時間步“t-1”的記憶狀態，維度為(n_a, m) parameters -- 字典類型的變量，包含了： Wf -- 遺忘門的權值，維度為(n_a, n_a + n_x) bf -- 遺忘門的偏置，維度為(n_a, 1) Wi -- 更新門的權值，維度為(n_a, n_a + n_x) bi -- 更新門的偏置，維度為(n_a, 1) Wc -- 第一個“tanh”的權值，維度為(n_a, n_a + n_x) bc -- 第一個“tanh”的偏置，維度為(n_a, n_a + n_x) Wo -- 輸出門的權值，維度為(n_a, n_a + n_x) bo -- 輸出門的偏置，維度為(n_a, 1) Wy -- 隱藏狀態與輸出相關的權值，維度為(n_y, n_a) by -- 隱藏狀態與輸出相關的偏置，維度為(n_y, 1) 返回： a_next -- 下一個隱藏狀態，維度為(n_a, m) c_next -- 下一個記憶狀態，維度為(n_a, m) yt_pred -- 在時間步“t”的預測，維度為(n_y, m) cache -- 包含了反向傳播所需要的參數，包含了(a_next, c_next, a_prev, c_prev, xt, parameters) 注意： ft/it/ot表示遺忘/更新/輸出門，cct表示候選值(c tilda)，c表示記憶值。 """
# 從“parameters”中獲取相關值
Wf = parameters["Wf"]
bf = parameters["bf"]
Wi = parameters["Wi"]
bi = parameters["bi"]
Wc = parameters["Wc"]
bc = parameters["bc"]
Wo = parameters["Wo"]
bo = parameters["bo"]
Wy = parameters["Wy"]
by = parameters["by"]
# 獲取 xt 與 Wy 的維度信息
n_x, m = xt.shape
n_y, n_a = Wy.shape
# 1.連接 a_prev 與 xt
contact = np.zeros([n_a + n_x, m])
contact[: n_a, :] = a_prev
contact[n_a :, :] = xt
# 2.根據公式計算ft、it、cct、c_next、ot、a_next
## 遺忘門，公式1
ft = rnn_utils.sigmoid(np.dot(Wf, contact) + bf)
## 更新門，公式2
it = rnn_utils.sigmoid(np.dot(Wi, contact) + bi)
## 更新單元，公式3
cct = np.tanh(np.dot(Wc, contact) + bc)
## 更新單元，公式4
#c_next = np.multiply(ft, c_prev) + np.multiply(it, cct)
c_next = ft * c_prev + it * cct
## 輸出門，公式5
ot = rnn_utils.sigmoid(np.dot(Wo, contact) + bo)
## 輸出門，公式6
#a_next = np.multiply(ot, np.tan(c_next))
a_next = ot * np.tanh(c_next)
# 3.計算LSTM單元的預測值
yt_pred = rnn_utils.softmax(np.dot(Wy, a_next) + by)
# 保存包含了反向傳播所需要的參數
cache = (a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters)
return a_next, c_next, yt_pred, cache

np.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
c_prev = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)
Wy = np.random.randn(2,5)
by = np.random.randn(2,1)
parameters = {
"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}
a_next, c_next, yt, cache = lstm_cell_forward(xt, a_prev, c_prev, parameters)
print("a_next[4] = ", a_next[4])
print("a_next.shape = ", c_next.shape)
print("c_next[2] = ", c_next[2])
print("c_next.shape = ", c_next.shape)
print("yt[1] =", yt[1])
print("yt.shape = ", yt.shape)
print("cache[1][3] =", cache[1][3])
print("len(cache) = ", len(cache))

a_next[4] = [-0.66408471 0.0036921 0.02088357 0.22834167 -0.85575339 0.00138482
0.76566531 0.34631421 -0.00215674 0.43827275]
a_next.shape = (5, 10)
c_next[2] = [ 0.63267805 1.00570849 0.35504474 0.20690913 -1.64566718 0.11832942
0.76449811 -0.0981561 -0.74348425 -0.26810932]
c_next.shape = (5, 10)
yt[1] = [0.79913913 0.15986619 0.22412122 0.15606108 0.97057211 0.31146381
0.00943007 0.12666353 0.39380172 0.07828381]
yt.shape = (2, 10)
cache[1][3] = [-0.16263996 1.03729328 0.72938082 -0.54101719 0.02752074 -0.30821874
0.07651101 -1.03752894 1.41219977 -0.37647422]
len(cache) = 10

2.2 LSTM的正向傳播

既然你已經實現了LSTM的一個步驟，現在就可以使用for循環在 T x T_x Tx​輸入序列上對此進行迭代。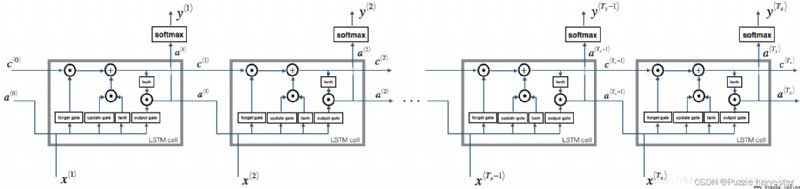

練習：實現lstm_forward()以在 T x T_x Tx​個時間步上運行LSTM。

注意: c * 0 * c^{\langle 0 \rangle} c*0*用零初始化。

def lstm_forward(x, a0, parameters):
""" 根據圖5來實現LSTM單元組成的的循環神經網絡 參數： x -- 所有時間步的輸入數據，維度為(n_x, m, T_x) a0 -- 初始化隱藏狀態，維度為(n_a, m) parameters -- python字典，包含了以下參數： Wf -- 遺忘門的權值，維度為(n_a, n_a + n_x) bf -- 遺忘門的偏置，維度為(n_a, 1) Wi -- 更新門的權值，維度為(n_a, n_a + n_x) bi -- 更新門的偏置，維度為(n_a, 1) Wc -- 第一個“tanh”的權值，維度為(n_a, n_a + n_x) bc -- 第一個“tanh”的偏置，維度為(n_a, n_a + n_x) Wo -- 輸出門的權值，維度為(n_a, n_a + n_x) bo -- 輸出門的偏置，維度為(n_a, 1) Wy -- 隱藏狀態與輸出相關的權值，維度為(n_y, n_a) by -- 隱藏狀態與輸出相關的偏置，維度為(n_y, 1) 返回： a -- 所有時間步的隱藏狀態，維度為(n_a, m, T_x) y -- 所有時間步的預測值，維度為(n_y, m, T_x) caches -- 為反向傳播的保存的元組，維度為（【列表類型】cache, x)） """
# 初始化“caches”
caches = []
# 獲取 xt 與 Wy 的維度信息
n_x, m, T_x = x.shape
n_y, n_a = parameters["Wy"].shape
# 使用0來初始化“a”、“c”、“y”
a = np.zeros([n_a, m, T_x])
c = np.zeros([n_a, m, T_x])
y = np.zeros([n_y, m, T_x])
# 初始化“a_next”、“c_next”
a_next = a0
c_next = np.zeros([n_a, m])
# 遍歷所有的時間步
for t in range(T_x):
# 更新下一個隱藏狀態，下一個記憶狀態，計算預測值，獲取cache
a_next, c_next, yt_pred, cache = lstm_cell_forward(x[:,:,t], a_next, c_next, parameters)
# 保存新的下一個隱藏狀態到變量a中
a[:, :, t] = a_next
# 保存預測值到變量y中
y[:, :, t] = yt_pred
# 保存下一個單元狀態到變量c中
c[:, :, t] = c_next
# 把cache添加到caches中
caches.append(cache)
# 保存反向傳播需要的參數
caches = (caches, x)
return a, y, c, caches

np.random.seed(1)
x = np.random.randn(3,10,7)
a0 = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)
Wy = np.random.randn(2,5)
by = np.random.randn(2,1)
parameters = {
"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}
a, y, c, caches = lstm_forward(x, a0, parameters)
print("a[4][3][6] = ", a[4][3][6])
print("a.shape = ", a.shape)
print("y[1][4][3] =", y[1][4][3])
print("y.shape = ", y.shape)
print("caches[1][1[1]] =", caches[1][1][1])
print("c[1][2][1]", c[1][2][1])
print("len(caches) = ", len(caches))

a[4][3][6] = 0.17211776753291672
a.shape = (5, 10, 7)
y[1][4][3] = 0.9508734618501101
y.shape = (2, 10, 7)
caches[1][1[1]] = [ 0.82797464 0.23009474 0.76201118 -0.22232814 -0.20075807 0.18656139
0.41005165]
c[1][2][1] -0.8555449167181981
len(caches) = 2

3 循環神經網絡中的反向傳播

在現代深度學習框架中，你僅需實現正向傳播，而框架將處理反向傳播，因此大多數深度學習工程師無需理會反向傳播的細節。但是，如果你是微積分專家並且想查看RNN中反向傳播的詳細信息，則可以學習此筆記本的剩余部分。

在較早的課程中，當你實現了一個簡單的（全連接的）神經網絡時，你就使用了反向傳播來計算用於更新參數的損失的導數。同樣，在循環神經網絡中，你可以計算損失的導數以更新參數。反向傳播方程非常復雜，我們在講座中沒有導出它們。但是，我們將在下面簡要介紹它們。

3.1 基礎RNN的反向傳播

我們將從計算基本RNN單元的反向傳播開始。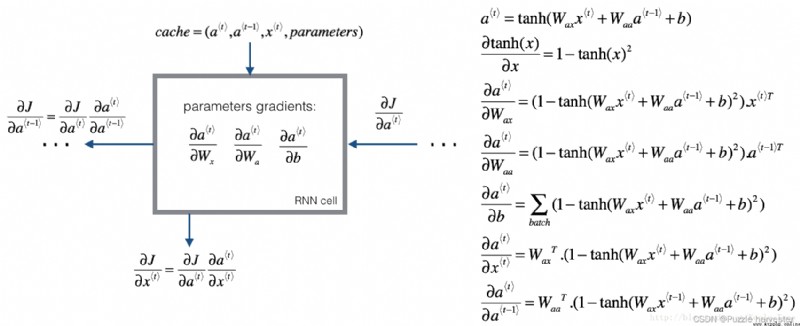

就像在全連接的神經網絡中一樣，損失函數 J J J的導數遵循鏈規則在RNN中計算反向傳播。鏈規則還用於計算 ( ∂ J ∂ W a x , ∂ J ∂ W a a , ∂ J ∂ b ) (\frac{\partial J}{\partial W_{ax}},\frac{\partial J}{\partial W_{aa}},\frac{\partial J}{\partial b}) (∂Wax​∂J​,∂Waa​∂J​,∂b∂J​)更新參數 ( W a x , W a a , b a ) (W_{ax}, W_{aa}, b_a) (Wax​,Waa​,ba​)。

3.1.1 反向求導函數：

要計算rnn_cell_backward，你需要計算以下方程式。手工導出它們是一個很好的練習。

tanh ⁡ \tanh tanh的導數為 1 − tanh ⁡ ( x ) 2 1-\tanh(x)^2 1−tanh(x)2。你可以在here中找到完整的證明。請注意：$ \text{sech}(x)^2 = 1 - \tanh(x)^2$

同樣，對於 ∂ a * t * ∂ W a x , ∂ a * t * ∂ W a a , ∂ a * t * ∂ b \frac{ \partial a^{\langle t \rangle} } {\partial W_{ax}}, \frac{ \partial a^{\langle t \rangle} } {\partial W_{aa}}, \frac{ \partial a^{\langle t \rangle} } {\partial b} ∂Wax​∂a*t*​,∂Waa​∂a*t*​,∂b∂a*t*​， tanh ⁡ ( u ) \tanh(u) tanh(u)導數為 ( 1 − tanh ⁡ ( u ) 2 ) d u (1-\tanh(u)^2)du (1−tanh(u)2)du。

最後兩個方程式也遵循相同的規則，並使用 tanh ⁡ \tanh tanh導數導出。請注意，這種安排是為了獲得相同的維度以方便匹配的。

def rnn_cell_backward(da_next, cache):
""" 實現基本的RNN單元的單步反向傳播 參數： da_next -- 關於下一個隱藏狀態的損失的梯度。 cache -- 字典類型，rnn_step_forward()的輸出 返回： gradients -- 字典，包含了以下參數： dx -- 輸入數據的梯度，維度為(n_x, m) da_prev -- 上一隱藏層的隱藏狀態，維度為(n_a, m) dWax -- 輸入到隱藏狀態的權重的梯度，維度為(n_a, n_x) dWaa -- 隱藏狀態到隱藏狀態的權重的梯度，維度為(n_a, n_a) dba -- 偏置向量的梯度，維度為(n_a, 1) """
# 獲取cache 的值
a_next, a_prev, xt, parameters = cache
# 從 parameters 中獲取參數
Wax = parameters["Wax"]
Waa = parameters["Waa"]
Wya = parameters["Wya"]
ba = parameters["ba"]
by = parameters["by"]
# 計算tanh相對於a_next的梯度.
dtanh = (1 - np.square(a_next)) * da_next
# 計算關於Wax損失的梯度
dxt = np.dot(Wax.T,dtanh)
dWax = np.dot(dtanh, xt.T)
# 計算關於Waa損失的梯度
da_prev = np.dot(Waa.T,dtanh)
dWaa = np.dot(dtanh, a_prev.T)
# 計算關於b損失的梯度
dba = np.sum(dtanh, keepdims=True, axis=-1)
# 保存這些梯度到字典內
gradients = {
"dxt": dxt, "da_prev": da_prev, "dWax": dWax, "dWaa": dWaa, "dba": dba}
return gradients

np.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
Wax = np.random.randn(5,3)
Waa = np.random.randn(5,5)
Wya = np.random.randn(2,5)
b = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {
"Wax": Wax, "Waa": Waa, "Wya": Wya, "ba": ba, "by": by}
a_next, yt, cache = rnn_cell_forward(xt, a_prev, parameters)
da_next = np.random.randn(5,10)
gradients = rnn_cell_backward(da_next, cache)
print("gradients[\"dxt\"][1][2] =", gradients["dxt"][1][2])
print("gradients[\"dxt\"].shape =", gradients["dxt"].shape)
print("gradients[\"da_prev\"][2][3] =", gradients["da_prev"][2][3])
print("gradients[\"da_prev\"].shape =", gradients["da_prev"].shape)
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWax\"].shape =", gradients["dWax"].shape)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWaa\"].shape =", gradients["dWaa"].shape)
print("gradients[\"dba\"][4] =", gradients["dba"][4])
print("gradients[\"dba\"].shape =", gradients["dba"].shape)

gradients["dxt"][1][2] = -0.4605641030588796
gradients["dxt"].shape = (3, 10)
gradients["da_prev"][2][3] = 0.08429686538067718
gradients["da_prev"].shape = (5, 10)
gradients["dWax"][3][1] = 0.3930818739219304
gradients["dWax"].shape = (5, 3)
gradients["dWaa"][1][2] = -0.2848395578696067
gradients["dWaa"].shape = (5, 5)
gradients["dba"][4] = [0.80517166]
gradients["dba"].shape = (5, 1)

3.1.2 反向傳播

在每個時間步長 t t t上計算相對於 a * t * a^{\langle t \rangle} a*t*的損失梯度非常有用，因為它有助於將梯度反向傳播到先前的RNN單元。為此，你需要從頭開始遍歷所有時間步，並且在每一步中，增加總的 d b a db_a dba​, d W a a dW_{aa} dWaa​, d W a x dW_{ax} dWax​並存儲 d x dx dx。

說明：
實現rnn_backward函數。首先用零初始化返回變量，然後循環遍歷所有時間步，同時在每個時間步調用rnn_cell_backward，相應地更新其他變量。

def rnn_backward(da, caches):
""" 在整個輸入數據序列上實現RNN的反向傳播 參數： da -- 所有隱藏狀態的梯度，維度為(n_a, m, T_x) caches -- 包含向前傳播的信息的元組 返回： gradients -- 包含了梯度的字典： dx -- 關於輸入數據的梯度，維度為(n_x, m, T_x) da0 -- 關於初始化隱藏狀態的梯度，維度為(n_a, m) dWax -- 關於輸入權重的梯度，維度為(n_a, n_x) dWaa -- 關於隱藏狀態的權值的梯度，維度為(n_a, n_a) dba -- 關於偏置的梯度，維度為(n_a, 1) """
# 從caches中獲取第一個cache（t=1）的值
caches, x = caches
a1, a0, x1, parameters = caches[0]
# 獲取da與x1的維度信息
n_a, m, T_x = da.shape
n_x, m = x1.shape
# 初始化梯度
dx = np.zeros([n_x, m, T_x])
dWax = np.zeros([n_a, n_x])
dWaa = np.zeros([n_a, n_a])
dba = np.zeros([n_a, 1])
da0 = np.zeros([n_a, m])
da_prevt = np.zeros([n_a, m])
# 處理所有時間步
for t in reversed(range(T_x)):
# 計算時間步“t”時的梯度
gradients = rnn_cell_backward(da[:, :, t] + da_prevt, caches[t])
#從梯度中獲取導數
dxt, da_prevt, dWaxt, dWaat, dbat = gradients["dxt"], gradients["da_prev"], gradients["dWax"], gradients["dWaa"], gradients["dba"]
# 通過在時間步t添加它們的導數來增加關於全局導數的參數
dx[:, :, t] = dxt
dWax += dWaxt
dWaa += dWaat
dba += dbat
#將 da0設置為a的梯度，該梯度已通過所有時間步驟進行反向傳播
da0 = da_prevt
#保存這些梯度到字典內
gradients = {
"dx": dx, "da0": da0, "dWax": dWax, "dWaa": dWaa,"dba": dba}
return gradients

np.random.seed(1)
x = np.random.randn(3,10,4)
a0 = np.random.randn(5,10)
Wax = np.random.randn(5,3)
Waa = np.random.randn(5,5)
Wya = np.random.randn(2,5)
ba = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {
"Wax": Wax, "Waa": Waa, "Wya": Wya, "ba": ba, "by": by}
a, y, caches = rnn_forward(x, a0, parameters)
da = np.random.randn(5, 10, 4)
gradients = rnn_backward(da, caches)
print("gradients[\"dx\"][1][2] =", gradients["dx"][1][2])
print("gradients[\"dx\"].shape =", gradients["dx"].shape)
print("gradients[\"da0\"][2][3] =", gradients["da0"][2][3])
print("gradients[\"da0\"].shape =", gradients["da0"].shape)
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWax\"].shape =", gradients["dWax"].shape)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWaa\"].shape =", gradients["dWaa"].shape)
print("gradients[\"dba\"][4] =", gradients["dba"][4])
print("gradients[\"dba\"].shape =", gradients["dba"].shape)

gradients["dx"][1][2] = [-2.07101689 -0.59255627 0.02466855 0.01483317]
gradients["dx"].shape = (3, 10, 4)
gradients["da0"][2][3] = -0.31494237512664996
gradients["da0"].shape = (5, 10)
gradients["dWax"][3][1] = 11.264104496527777
gradients["dWax"].shape = (5, 3)
gradients["dWaa"][1][2] = 2.3033331265798935
gradients["dWaa"].shape = (5, 5)
gradients["dba"][4] = [-0.74747722]
gradients["dba"].shape = (5, 1)

3.2 LSTM反向傳播

3.2.1 反向傳播一步

LSTM反向傳播比正向傳播要復雜得多。我們在下面為你提供了LSTM反向傳播的所有方程式。（如果你喜歡微積分練習，可以嘗試從頭開始自己演算）

3.2.2 門求導

d Γ o * t * = d a n e x t ∗ tanh ⁡ ( c n e x t ) ∗ Γ o * t * ∗ ( 1 − Γ o * t * ) (7) d \Gamma_o^{\langle t \rangle} = da_{next}*\tanh(c_{next}) * \Gamma_o^{\langle t \rangle}*(1-\Gamma_o^{\langle t \rangle})\tag{7} dΓo*t*​=danext​∗tanh(cnext​)∗Γo*t*​∗(1−Γo*t*​)(7)

d c ~ * t * = ( d c n e x t ∗ Γ u * t * + Γ o * t * ( 1 − tanh ⁡ ( c n e x t ) 2 ) ∗ i t ∗ d a n e x t ∗ c ~ * t * ) ∗ ( 1 − tanh ⁡ ( c ~ ) 2 ) (8) d\tilde c^{\langle t \rangle} = (dc_{next}*\Gamma_u^{\langle t \rangle}+ \Gamma_o^{\langle t \rangle} (1-\tanh(c_{next})^2) * i_t * da_{next} * \tilde c^{\langle t \rangle}) * (1-\tanh(\tilde c)^2) \tag{8} dc~*t*=(dcnext​∗Γu*t*​+Γo*t*​(1−tanh(cnext​)2)∗it​∗danext​∗c~*t*)∗(1−tanh(c~)2)(8)

d Γ u * t * = ( d c n e x t ∗ c ~ * t * + Γ o * t * ( 1 − tanh ⁡ ( c n e x t ) 2 ) ∗ c ~ * t * ∗ d a n e x t ) ∗ Γ u * t * ∗ ( 1 − Γ u * t * ) (9) d\Gamma_u^{\langle t \rangle} = (dc_{next}*\tilde c^{\langle t \rangle} + \Gamma_o^{\langle t \rangle} (1-\tanh(c_{next})^2) * \tilde c^{\langle t \rangle} * da_{next})*\Gamma_u^{\langle t \rangle}*(1-\Gamma_u^{\langle t \rangle})\tag{9} dΓu*t*​=(dcnext​∗c~*t*+Γo*t*​(1−tanh(cnext​)2)∗c~*t*∗danext​)∗Γu*t*​∗(1−Γu*t*​)(9)

d Γ f * t * = ( d c n e x t ∗ c ~ p r e v + Γ o * t * ( 1 − tanh ⁡ ( c n e x t ) 2 ) ∗ c p r e v ∗ d a n e x t ) ∗ Γ f * t * ∗ ( 1 − Γ f * t * ) (10) d\Gamma_f^{\langle t \rangle} = (dc_{next}*\tilde c_{prev} + \Gamma_o^{\langle t \rangle} (1-\tanh(c_{next})^2) * c_{prev} * da_{next})*\Gamma_f^{\langle t \rangle}*(1-\Gamma_f^{\langle t \rangle})\tag{10} dΓf*t*​=(dcnext​∗c~prev​+Γo*t*​(1−tanh(cnext​)2)∗cprev​∗danext​)∗Γf*t*​∗(1−Γf*t*​)(10)

3.2.3 參數求導

d W f = d Γ f * t * ∗ ( a p r e v x t ) T (11) dW_f = d\Gamma_f^{\langle t \rangle} * \begin{pmatrix} a_{prev} \\ x_t\end{pmatrix}^T \tag{11} dWf​=dΓf*t*​∗(aprev​xt​​)T(11)
d W u = d Γ u * t * ∗ ( a p r e v x t ) T (12) dW_u = d\Gamma_u^{\langle t \rangle} * \begin{pmatrix} a_{prev} \\ x_t\end{pmatrix}^T \tag{12} dWu​=dΓu*t*​∗(aprev​xt​​)T(12)
d W c = d c ~ * t * ∗ ( a p r e v x t ) T (13) dW_c = d\tilde c^{\langle t \rangle} * \begin{pmatrix} a_{prev} \\ x_t\end{pmatrix}^T \tag{13} dWc​=dc~*t*∗(aprev​xt​​)T(13)
d W o = d Γ o * t * ∗ ( a p r e v x t ) T (14) dW_o = d\Gamma_o^{\langle t \rangle} * \begin{pmatrix} a_{prev} \\ x_t\end{pmatrix}^T \tag{14} dWo​=dΓo*t*​∗(aprev​xt​​)T(14)
要計算 d b f , d b u , d b c , d b o db_f, db_u, db_c, db_o dbf​,dbu​,dbc​,dbo​，你只需要在 d Γ f * t * , d Γ u * t * , d c ~ * t * , d Γ o * t * d\Gamma_f^{\langle t \rangle}, d\Gamma_u^{\langle t \rangle}, d\tilde c^{\langle t \rangle}, d\Gamma_o^{\langle t \rangle} dΓf*t*​,dΓu*t*​,dc~*t*,dΓo*t*​的水平（axis=1）軸上分別求和。注意，你應該有keep_dims = True選項。

最後，你將針對先前的隱藏狀態，先前的記憶狀態和輸入計算導數。
d a p r e v = W f T ∗ d Γ f * t * + W u T ∗ d Γ u * t * + W c T ∗ d c ~ * t * + W o T ∗ d Γ o * t * (15) da_{prev} = W_f^T*d\Gamma_f^{\langle t \rangle} + W_u^T * d\Gamma_u^{\langle t \rangle}+ W_c^T * d\tilde c^{\langle t \rangle} + W_o^T * d\Gamma_o^{\langle t \rangle} \tag{15} daprev​=WfT​∗dΓf*t*​+WuT​∗dΓu*t*​+WcT​∗dc~*t*+WoT​∗dΓo*t*​(15)
在這裡，等式13的權重是第n_a個（即 W f = W f [ : , : n a ] W_f = W_f[:,:n_a] Wf​=Wf​[:,:na​]等…）
d c p r e v = d c n e x t Γ f * t * + Γ o * t * ∗ ( 1 − tanh ⁡ ( c n e x t ) 2 ) ∗ Γ f * t * ∗ d a n e x t (16) dc_{prev} = dc_{next}\Gamma_f^{\langle t \rangle} + \Gamma_o^{\langle t \rangle} * (1- \tanh(c_{next})^2)*\Gamma_f^{\langle t \rangle}*da_{next} \tag{16} dcprev​=dcnext​Γf*t*​+Γo*t*​∗(1−tanh(cnext​)2)∗Γf*t*​∗danext​(16)
d x * t * = W f T ∗ d Γ f * t * + W u T ∗ d Γ u * t * + W c T ∗ d c ~ t + W o T ∗ d Γ o * t * (17) dx^{\langle t \rangle} = W_f^T*d\Gamma_f^{\langle t \rangle} + W_u^T * d\Gamma_u^{\langle t \rangle}+ W_c^T * d\tilde c_t + W_o^T * d\Gamma_o^{\langle t \rangle}\tag{17} dx*t*=WfT​∗dΓf*t*​+WuT​∗dΓu*t*​+WcT​∗dc~t​+WoT​∗dΓo*t*​(17)
其中等式15的權重是從n_a到末尾（即 W f = W f [ : , n a : ] W_f = W_f[:,n_a:] Wf​=Wf​[:,na​:]等…）

練習：通過實現下面的等式來實現lstm_cell_backward。

def lstm_cell_backward(da_next, dc_next, cache):
""" 實現LSTM的單步反向傳播 參數： da_next -- 下一個隱藏狀態的梯度，維度為(n_a, m) dc_next -- 下一個單元狀態的梯度，維度為(n_a, m) cache -- 來自前向傳播的一些參數 返回： gradients -- 包含了梯度信息的字典： dxt -- 輸入數據的梯度，維度為(n_x, m) da_prev -- 先前的隱藏狀態的梯度，維度為(n_a, m) dc_prev -- 前的記憶狀態的梯度，維度為(n_a, m, T_x) dWf -- 遺忘門的權值的梯度，維度為(n_a, n_a + n_x) dbf -- 遺忘門的偏置的梯度，維度為(n_a, 1) dWi -- 更新門的權值的梯度，維度為(n_a, n_a + n_x) dbi -- 更新門的偏置的梯度，維度為(n_a, 1) dWc -- 第一個“tanh”的權值的梯度，維度為(n_a, n_a + n_x) dbc -- 第一個“tanh”的偏置的梯度，維度為(n_a, n_a + n_x) dWo -- 輸出門的權值的梯度，維度為(n_a, n_a + n_x) dbo -- 輸出門的偏置的梯度，維度為(n_a, 1) """
# 從cache中獲取信息
(a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters) = cache
# 獲取xt與a_next的維度信息
n_x, m = xt.shape
n_a, m = a_next.shape
# 根據公式7-10來計算門的導數
dot = da_next * np.tanh(c_next) * ot * (1 - ot)
dcct = (dc_next * it + ot * (1 - np.square(np.tanh(c_next))) * it * da_next) * (1 - np.square(cct))
dit = (dc_next * cct + ot * (1 - np.square(np.tanh(c_next))) * cct * da_next) * it * (1 - it)
dft = (dc_next * c_prev + ot * (1 - np.square(np.tanh(c_next))) * c_prev * da_next) * ft * (1 - ft)
# 根據公式11-14計算參數的導數
concat = np.concatenate((a_prev, xt), axis=0).T
dWf = np.dot(dft, concat)
dWi = np.dot(dit, concat)
dWc = np.dot(dcct, concat)
dWo = np.dot(dot, concat)
dbf = np.sum(dft,axis=1,keepdims=True)
dbi = np.sum(dit,axis=1,keepdims=True)
dbc = np.sum(dcct,axis=1,keepdims=True)
dbo = np.sum(dot,axis=1,keepdims=True)
# 使用公式15-17計算洗起來了隱藏狀態、先前記憶狀態、輸入的導數。
da_prev = np.dot(parameters["Wf"][:, :n_a].T, dft) + np.dot(parameters["Wc"][:, :n_a].T, dcct) + np.dot(parameters["Wi"][:, :n_a].T, dit) + np.dot(parameters["Wo"][:, :n_a].T, dot)
dc_prev = dc_next * ft + ot * (1 - np.square(np.tanh(c_next))) * ft * da_next
dxt = np.dot(parameters["Wf"][:, n_a:].T, dft) + np.dot(parameters["Wc"][:, n_a:].T, dcct) + np.dot(parameters["Wi"][:, n_a:].T, dit) + np.dot(parameters["Wo"][:, n_a:].T, dot)
# 保存梯度信息到字典
gradients = {
"dxt": dxt, "da_prev": da_prev, "dc_prev": dc_prev, "dWf": dWf,"dbf": dbf, "dWi": dWi,"dbi": dbi,
"dWc": dWc,"dbc": dbc, "dWo": dWo,"dbo": dbo}
return gradients

np.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
c_prev = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)
Wy = np.random.randn(2,5)
by = np.random.randn(2,1)
parameters = {
"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}
a_next, c_next, yt, cache = lstm_cell_forward(xt, a_prev, c_prev, parameters)
da_next = np.random.randn(5,10)
dc_next = np.random.randn(5,10)
gradients = lstm_cell_backward(da_next, dc_next, cache)
print("gradients[\"dxt\"][1][2] =", gradients["dxt"][1][2])
print("gradients[\"dxt\"].shape =", gradients["dxt"].shape)
print("gradients[\"da_prev\"][2][3] =", gradients["da_prev"][2][3])
print("gradients[\"da_prev\"].shape =", gradients["da_prev"].shape)
print("gradients[\"dc_prev\"][2][3] =", gradients["dc_prev"][2][3])
print("gradients[\"dc_prev\"].shape =", gradients["dc_prev"].shape)
print("gradients[\"dWf\"][3][1] =", gradients["dWf"][3][1])
print("gradients[\"dWf\"].shape =", gradients["dWf"].shape)
print("gradients[\"dWi\"][1][2] =", gradients["dWi"][1][2])
print("gradients[\"dWi\"].shape =", gradients["dWi"].shape)
print("gradients[\"dWc\"][3][1] =", gradients["dWc"][3][1])
print("gradients[\"dWc\"].shape =", gradients["dWc"].shape)
print("gradients[\"dWo\"][1][2] =", gradients["dWo"][1][2])
print("gradients[\"dWo\"].shape =", gradients["dWo"].shape)
print("gradients[\"dbf\"][4] =", gradients["dbf"][4])
print("gradients[\"dbf\"].shape =", gradients["dbf"].shape)
print("gradients[\"dbi\"][4] =", gradients["dbi"][4])
print("gradients[\"dbi\"].shape =", gradients["dbi"].shape)
print("gradients[\"dbc\"][4] =", gradients["dbc"][4])
print("gradients[\"dbc\"].shape =", gradients["dbc"].shape)
print("gradients[\"dbo\"][4] =", gradients["dbo"][4])
print("gradients[\"dbo\"].shape =", gradients["dbo"].shape)

gradients["dxt"][1][2] = 3.230559115109188
gradients["dxt"].shape = (3, 10)
gradients["da_prev"][2][3] = -0.06396214197109236
gradients["da_prev"].shape = (5, 10)
gradients["dc_prev"][2][3] = 0.7975220387970015
gradients["dc_prev"].shape = (5, 10)
gradients["dWf"][3][1] = -0.1479548381644968
gradients["dWf"].shape = (5, 8)
gradients["dWi"][1][2] = 1.0574980552259903
gradients["dWi"].shape = (5, 8)
gradients["dWc"][3][1] = 2.3045621636876668
gradients["dWc"].shape = (5, 8)
gradients["dWo"][1][2] = 0.3313115952892109
gradients["dWo"].shape = (5, 8)
gradients["dbf"][4] = [0.18864637]
gradients["dbf"].shape = (5, 1)
gradients["dbi"][4] = [-0.40142491]
gradients["dbi"].shape = (5, 1)
gradients["dbc"][4] = [0.25587763]
gradients["dbc"].shape = (5, 1)
gradients["dbo"][4] = [0.13893342]
gradients["dbo"].shape = (5, 1)

3.3 反向傳播LSTM RNN

這部分與你在上面實現的rnn_backward函數非常相似。首先將創建與返回變量相同維度的變量。然後，你將從頭開始遍歷所有時間步，並在每次迭代中調用為LSTM實現的一步函數。然後，你將通過分別匯總參數來更新參數。最後返回帶有新梯度的字典。

說明：實現lstm_backward函數。創建一個從 T x T_x Tx​開始並向後的for循環。對於每個步驟，請調用lstm_cell_backward並通過向其添加新梯度來更新舊梯度。請注意，dxt不會更新而是存儲。

def lstm_backward(da, caches):
""" 實現LSTM網絡的反向傳播 參數： da -- 關於隱藏狀態的梯度，維度為(n_a, m, T_x) cachses -- 前向傳播保存的信息 返回： gradients -- 包含了梯度信息的字典： dx -- 輸入數據的梯度，維度為(n_x, m，T_x) da0 -- 先前的隱藏狀態的梯度，維度為(n_a, m) dWf -- 遺忘門的權值的梯度，維度為(n_a, n_a + n_x) dbf -- 遺忘門的偏置的梯度，維度為(n_a, 1) dWi -- 更新門的權值的梯度，維度為(n_a, n_a + n_x) dbi -- 更新門的偏置的梯度，維度為(n_a, 1) dWc -- 第一個“tanh”的權值的梯度，維度為(n_a, n_a + n_x) dbc -- 第一個“tanh”的偏置的梯度，維度為(n_a, n_a + n_x) dWo -- 輸出門的權值的梯度，維度為(n_a, n_a + n_x) dbo -- 輸出門的偏置的梯度，維度為(n_a, 1) """
# 從caches中獲取第一個cache（t=1）的值
caches, x = caches
(a1, c1, a0, c0, f1, i1, cc1, o1, x1, parameters) = caches[0]
# 獲取da與x1的維度信息
n_a, m, T_x = da.shape
n_x, m = x1.shape
# 初始化梯度
dx = np.zeros([n_x, m, T_x])
da0 = np.zeros([n_a, m])
da_prevt = np.zeros([n_a, m])
dc_prevt = np.zeros([n_a, m])
dWf = np.zeros([n_a, n_a + n_x])
dWi = np.zeros([n_a, n_a + n_x])
dWc = np.zeros([n_a, n_a + n_x])
dWo = np.zeros([n_a, n_a + n_x])
dbf = np.zeros([n_a, 1])
dbi = np.zeros([n_a, 1])
dbc = np.zeros([n_a, 1])
dbo = np.zeros([n_a, 1])
# 處理所有時間步
for t in reversed(range(T_x)):
# 使用lstm_cell_backward函數計算所有梯度
gradients = lstm_cell_backward(da[:,:,t],dc_prevt,caches[t])
# 保存相關參數
dx[:,:,t] = gradients['dxt']
dWf = dWf+gradients['dWf']
dWi = dWi+gradients['dWi']
dWc = dWc+gradients['dWc']
dWo = dWo+gradients['dWo']
dbf = dbf+gradients['dbf']
dbi = dbi+gradients['dbi']
dbc = dbc+gradients['dbc']
dbo = dbo+gradients['dbo']
# 將第一個激活的梯度設置為反向傳播的梯度da_prev。
da0 = gradients['da_prev']
# 保存所有梯度到字典變量內
gradients = {
"dx": dx, "da0": da0, "dWf": dWf,"dbf": dbf, "dWi": dWi,"dbi": dbi,
"dWc": dWc,"dbc": dbc, "dWo": dWo,"dbo": dbo}
return gradients

np.random.seed(1)
x = np.random.randn(3,10,7)
a0 = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)
parameters = {
"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}
a, y, c, caches = lstm_forward(x, a0, parameters)
da = np.random.randn(5, 10, 4)
gradients = lstm_backward(da, caches)
print("gradients[\"dx\"][1][2] =", gradients["dx"][1][2])
print("gradients[\"dx\"].shape =", gradients["dx"].shape)
print("gradients[\"da0\"][2][3] =", gradients["da0"][2][3])
print("gradients[\"da0\"].shape =", gradients["da0"].shape)
print("gradients[\"dWf\"][3][1] =", gradients["dWf"][3][1])
print("gradients[\"dWf\"].shape =", gradients["dWf"].shape)
print("gradients[\"dWi\"][1][2] =", gradients["dWi"][1][2])
print("gradients[\"dWi\"].shape =", gradients["dWi"].shape)
print("gradients[\"dWc\"][3][1] =", gradients["dWc"][3][1])
print("gradients[\"dWc\"].shape =", gradients["dWc"].shape)
print("gradients[\"dWo\"][1][2] =", gradients["dWo"][1][2])
print("gradients[\"dWo\"].shape =", gradients["dWo"].shape)
print("gradients[\"dbf\"][4] =", gradients["dbf"][4])
print("gradients[\"dbf\"].shape =", gradients["dbf"].shape)
print("gradients[\"dbi\"][4] =", gradients["dbi"][4])
print("gradients[\"dbi\"].shape =", gradients["dbi"].shape)
print("gradients[\"dbc\"][4] =", gradients["dbc"][4])
print("gradients[\"dbc\"].shape =", gradients["dbc"].shape)
print("gradients[\"dbo\"][4] =", gradients["dbo"][4])
print("gradients[\"dbo\"].shape =", gradients["dbo"].shape)

gradients["dx"][1][2] = [-0.00173313 0.08287442 -0.30545663 -0.43281115]
gradients["dx"].shape = (3, 10, 4)
gradients["da0"][2][3] = -0.09591150195400468
gradients["da0"].shape = (5, 10)
gradients["dWf"][3][1] = -0.06981985612744009
gradients["dWf"].shape = (5, 8)
gradients["dWi"][1][2] = 0.10237182024854771
gradients["dWi"].shape = (5, 8)
gradients["dWc"][3][1] = -0.062498379492745226
gradients["dWc"].shape = (5, 8)
gradients["dWo"][1][2] = 0.04843891314443012
gradients["dWo"].shape = (5, 8)
gradients["dbf"][4] = [-0.0565788]
gradients["dbf"].shape = (5, 1)
gradients["dbi"][4] = [-0.15399065]
gradients["dbi"].shape = (5, 1)
gradients["dbc"][4] = [-0.29691142]
gradients["dbc"].shape = (5, 1)
gradients["dbo"][4] = [-0.29798344]
gradients["dbo"].shape = (5, 1)