熟悉掌握遺傳算法。
用遺傳算法求解 n 皇後問題。n*n 的棋盤上擺放 n 個皇後,兩個皇後如果在同一直線或者同一對角線就會互相攻擊。 找一種擺法,使得任意兩個皇後之間都不會互相攻擊。

問題描述:遺傳算法舉例:8 皇後問題
個體:長為 8 的序列,每一列的值代表對 應列的皇後所在的行。 右圖狀態:83742516
適應度函數= 28-互相攻擊的皇後對 的數目 (不互相攻擊的皇後對的數目)
好的狀態對應較大的適應度函數值 (min = 0, max = 8 × 7/2 = 28。
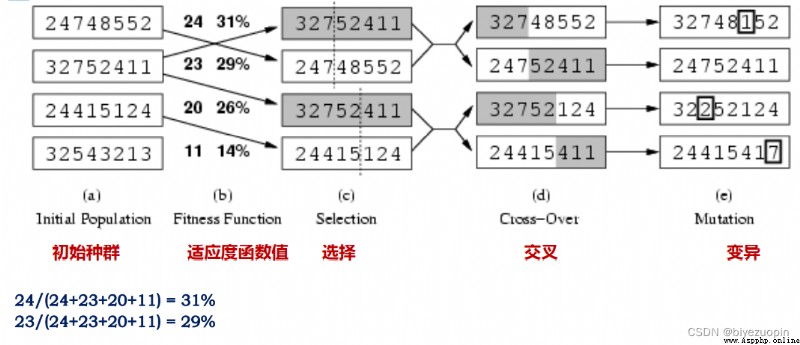
注意事項:
種群大小(每代的個體數量)設置:可嘗試 20,50,100。
迭代終止條件:對於八皇後問題,適應度函數達到 28(找到最優解)就可 以終止。也有可能你的算法寫的有問題,導致適應度函數值永遠無法到達 28,所以最好還是設一個最大迭代步數,或者當適應度函數值不發生變化 時終止迭代。
交叉率:0.5~1,不能太小 。
變異率:0.01~0.2,只允許少數個體變異,不能太大。
每一代最好將上一代中適應度函數值高的一些個體保留到下一代,這樣就 確保下一代的結果不會比上一代差。
最後的結果畫個簡單的 8 皇後擺放的圖。這樣才能看出是否有沖突。相當 於顯示一個 8*8 的矩陣,例如有皇後的地方顯示數字 8,其他地方顯示數字 0。
如果能解決 8 皇後問題,也可以嘗試 N 皇後問題(例如 N=32)。
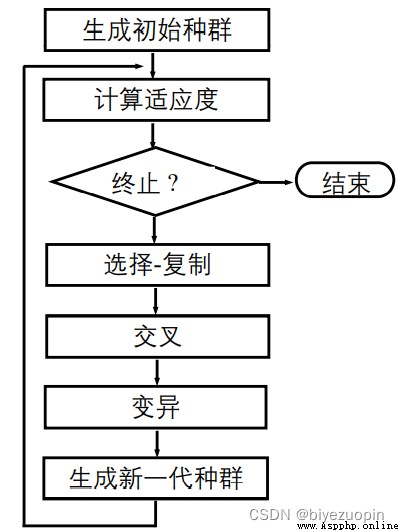
流程圖如下:
實驗設置:
初始化種群:手動輸入皇後的個數 n,初始化種群的大小為隨機數,范圍在 7n~13n 之間,根據皇後個數不一樣種群的大小范圍不一樣,皇後數越多種群的越大。
適應度函數:適應度函數= n*(n-1)/2-互相攻擊的皇後對的數目 (不互相攻擊的皇後對的數目)。由於題目的原因在因為每列僅僅一個數字,所以列不沖突;所以只需要檢查行和斜線上是否沖突。對於行上面,統計種群中每個個體重復出現的次數,在斜線上判斷某個位置上的橫坐標只差是否與縱坐標的之差的絕對值是否相等。
淘汰:適應度低的終將被淘汰。在 0.13~0.145 之間隨機產生一個數,適應度小於該數的會被淘汰,後來發現這個范圍不適用於所有的種群,種群小的淘汰的就少,種群大的淘汰就多,有時會出現種群所有個體全被淘汰的情況。 最後在後面處理加一個田間判斷當淘汰率大於 30% 時采取新的淘汰機制——所有的種群按適應度排序,適應度越低的 25% 將會被淘汰。為了保證種群的大小與原來相同,在沒有被淘汰的種群中隨機挑選與淘汰掉的數目相同的個體進行復制,然後打亂順序。
交叉互換:將適應度高的個體保留以保證子代的結果不會比父代差,比例為 5%;將所有個體與其對應的適應度以匹配起來,按照適應度進行排序,將排在前 5% 的保留到下一代並從父代中刪除,將父代順序打亂。隨機生成父代種群大小的一半個數,表示父代相鄰個體兩兩交叉互換的位置。
變異:在 0.01~0.04 之間隨機產生一個數作為變異率,便可以得到變異的個體數目 Mutation_num,隨機產生變異的 Mutation_num 個個體的變異位置 Mutationindexs,隨機產生 Mutation_num 個突變成的數字,將子代中的每個在 Mutationindexs 中位置發生突變
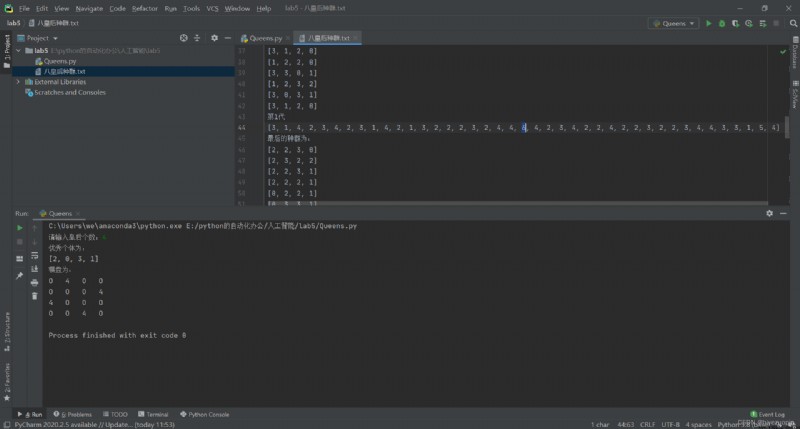
實驗運行過程及結果如下:
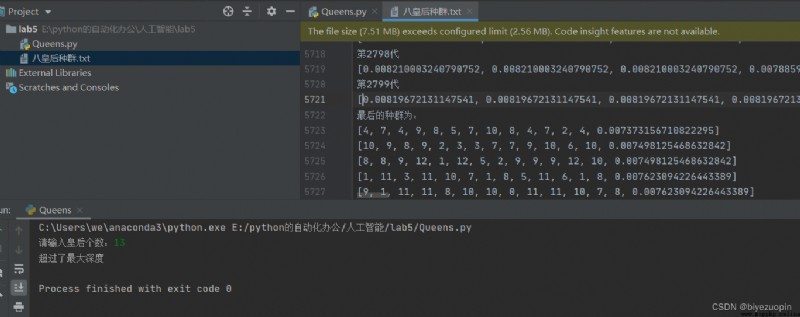
皇後互不打架:並用 text 文件存儲初始種群以及迭代過程的各個個體的適應度。以及最終種群。
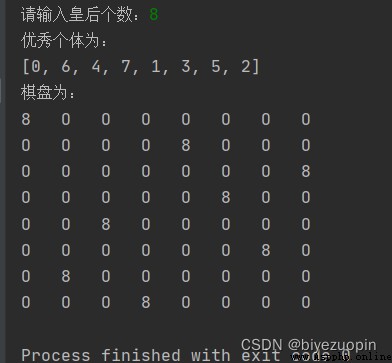
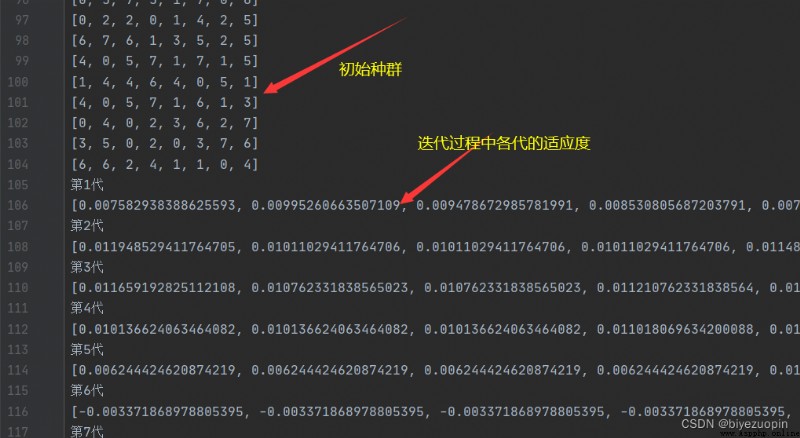
皇後互不打架:
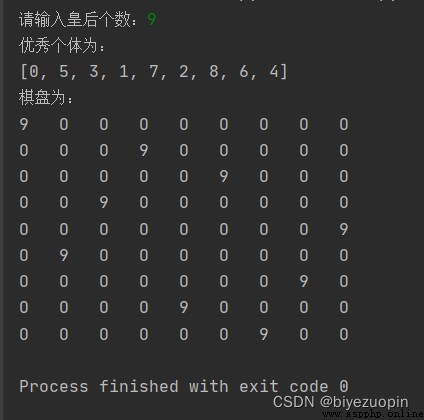
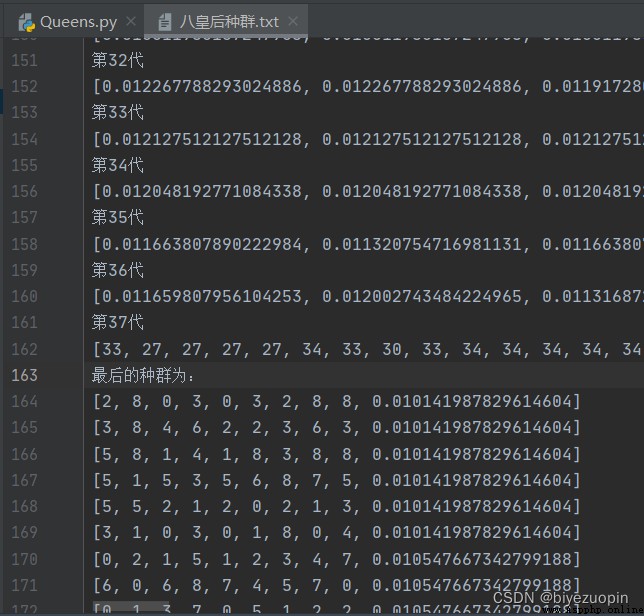
皇後互不打架:
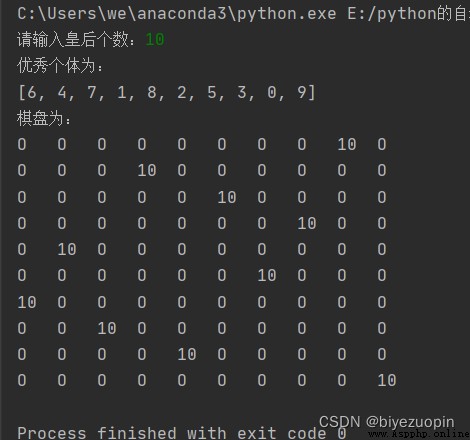
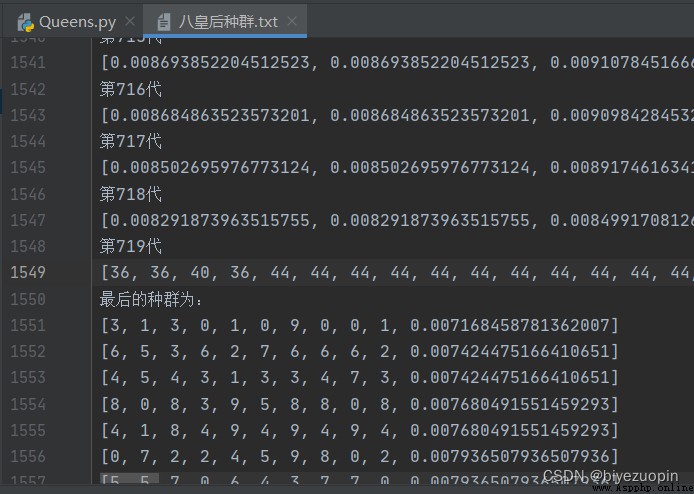
皇後互不打架:

皇後互不打架:
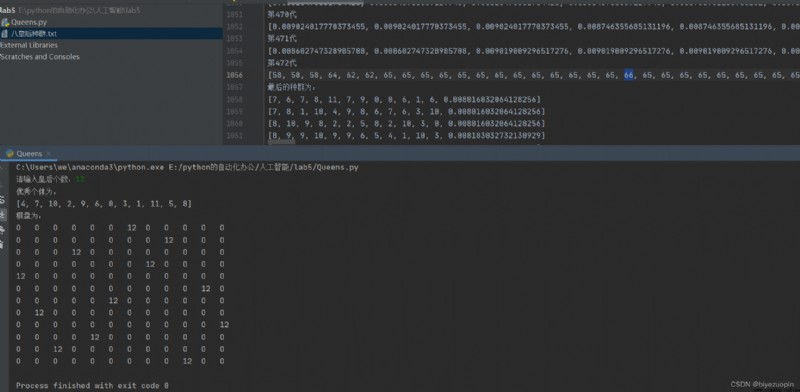
皇後
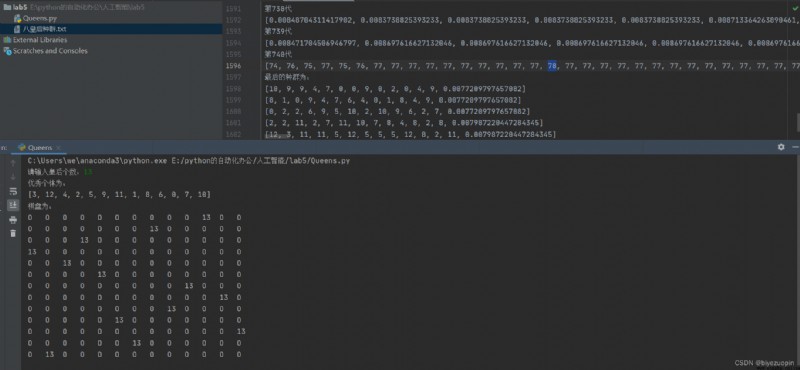
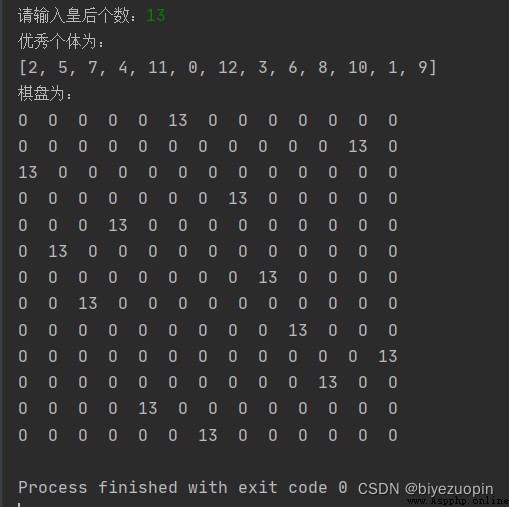
超過最大深度

皇後:第一代就成功了,記錄一下