您现在的位置：程式師世界 >> 編程語言 > >> 更多編程語言 >> Python

ROS python調用osqp庫的具體操作步驟

編輯：Python

odqp作為二次規劃庫具有非常重要的作用，可以運用於模型預測控制算法（MPC）

ROS C++庫調用方式可以參考這篇文章ROS c++調用osqp-eigen庫的具體操作步驟

按如下過程就能正常地在python中使用osqp庫。

准備工作

1.獲取測試程序

在這個例子中我所使用的是osqp官網的python程序，用來設計MPC控制器：

運用osqp求解MPC優化問題

2.放入功能包

將這個文件放入我們自己的功能包的scripts文件夾下：

右鍵屬性，允許作為可執行文件

osqp庫的調用

python調用osqp庫中會遇到一些問題，我的版本是Ubuntu18.04+ROSmelodic，默認的python版本是python2.7。安裝osqp會有如下提示：

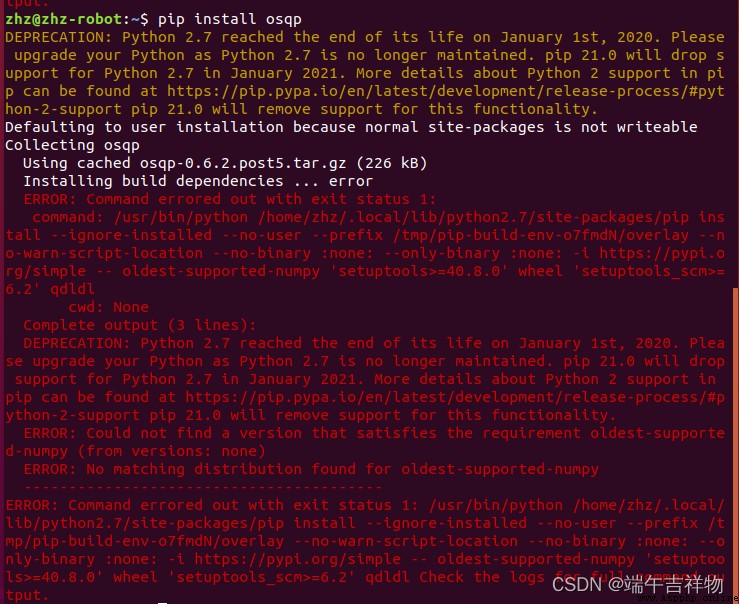
這說明python2.7版本已經不行了，需要更換解釋器，所以我打算換成python3.6解釋器。

接下來就是安裝步驟了

步驟1：安裝pip3

~$ sudo apt install python3-pip

步驟2：安裝osqp庫和其他需要的庫

~$ pip3 install osqp
~$ pip3 install catkin-tools
~$ pip3 install rospkg

我們可以查看osqp的安裝位置：

~$ pip show osqp

~$ pip3 show osqp
Name: osqp
Version: 0.6.2.post5
Summary: OSQP: The Operator Splitting QP Solver
Home-page: https://osqp.org/
Author: Bartolomeo Stellato, Goran Banjac
Author-email: [email protected]
License: Apache 2.0
Location: /home/zhz/.local/lib/python3.6/site-packages
Requires: numpy, scipy, qdldl

osqp庫保存在.local/lib/python3.6/site-packages中

步驟3：更改程序

編輯測試程序，將解釋器更換為python3或python3.6（具體看保存在python哪個版本中）

#!/usr/bin/env python3 ######更改解釋器為python3或者python3.6
# -*- coding=utf-8 -*-
import osqp
import numpy as np
import scipy as sp
from scipy import sparse

測試結果

1.常規測試

啟動roscore，命令行輸入

~$ rosrun <your_package_name> mpc_test_file.py

這裡我將時間步更改為3步，同時打印控制輸出的第一個元素，測試結果如下：

[email protected]:~$ rosrun path_track mpc_test_file.py
-----------------------------------------------------------------
OSQP v0.6.2 - Operator Splitting QP Solver
(c) Bartolomeo Stellato, Goran Banjac
University of Oxford - Stanford University 2021
-----------------------------------------------------------------
problem: variables n = 172, constraints m = 304
nnz(P) + nnz(A) = 1161
settings: linear system solver = qdldl,
eps_abs = 1.0e-03, eps_rel = 1.0e-03,
eps_prim_inf = 1.0e-04, eps_dual_inf = 1.0e-04,
rho = 1.00e-01 (adaptive),
sigma = 1.00e-06, alpha = 1.60, max_iter = 4000
check_termination: on (interval 25),
scaling: on, scaled_termination: off
warm start: on, polish: off, time_limit: off
iter objective pri res dua res rho time
1 -3.2965e+01 8.15e-01 6.00e+00 1.00e-01 4.15e-04s
25 -4.0983e+01 6.50e-05 2.15e-04 1.00e-01 6.08e-04s
status: solved
number of iterations: 25
optimal objective: -40.9834
run time: 6.49e-04s
optimal rho estimate: 9.40e-02
the first element of u(k) is %0.6 1.7484185677919
iter objective pri res dua res rho time
1 -4.0983e+01 1.67e+00 9.40e+02 1.00e-01 2.18e-05s
25 -4.6383e+01 4.50e-04 4.45e-03 1.00e-01 2.18e-04s
status: solved
number of iterations: 25
optimal objective: -46.3833
run time: 2.42e-04s
optimal rho estimate: 4.51e-02
the first element of u(k) is %0.6 0.5814805859402932
iter objective pri res dua res rho time
1 -4.6383e+01 9.59e-01 5.39e+02 1.00e-01 2.14e-05s
25 -5.0969e+01 2.47e-04 2.56e-03 1.00e-01 1.89e-04s
status: solved
number of iterations: 25
optimal objective: -50.9693
run time: 2.06e-04s
optimal rho estimate: 4.41e-02
the first element of u(k) is %0.6 0.008330435236109587
[email protected]:~$

2.ROS測試

在這個測試程序中加入ROS命令，發布話題，持續進行模型預測控制，測試程序如下：

#!/usr/bin/env python3
# -*- coding=utf-8 -*-
import rospy
import osqp
import numpy as np
import scipy as sp
from scipy import sparse
from std_msgs.msg import Float64
def publisher():
rospy.init_node('result_publisher',anonymous=True)
pub=rospy.Publisher('mpc_pub',Float64,queue_size=10)
rate=rospy.Rate(10)
# Discrete time model of a quadcopter
Ad = sparse.csc_matrix([
[1., 0., 0., 0., 0., 0., 0.1, 0., 0., 0., 0., 0. ],
[0., 1., 0., 0., 0., 0., 0., 0.1, 0., 0., 0., 0. ],
[0., 0., 1., 0., 0., 0., 0., 0., 0.1, 0., 0., 0. ],
[0.0488, 0., 0., 1., 0., 0., 0.0016, 0., 0., 0.0992, 0., 0. ],
[0., -0.0488, 0., 0., 1., 0., 0., -0.0016, 0., 0., 0.0992, 0. ],
[0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0.0992],
[0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0. ],
[0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0. ],
[0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0. ],
[0.9734, 0., 0., 0., 0., 0., 0.0488, 0., 0., 0.9846, 0., 0. ],
[0., -0.9734, 0., 0., 0., 0., 0., -0.0488, 0., 0., 0.9846, 0. ],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.9846]
])
Bd = sparse.csc_matrix([
[0., -0.0726, 0., 0.0726],
[-0.0726, 0., 0.0726, 0. ],
[-0.0152, 0.0152, -0.0152, 0.0152],
[-0., -0.0006, -0., 0.0006],
[0.0006, 0., -0.0006, 0.0000],
[0.0106, 0.0106, 0.0106, 0.0106],
[0, -1.4512, 0., 1.4512],
[-1.4512, 0., 1.4512, 0. ],
[-0.3049, 0.3049, -0.3049, 0.3049],
[-0., -0.0236, 0., 0.0236],
[0.0236, 0., -0.0236, 0. ],
[0.2107, 0.2107, 0.2107, 0.2107]])
[nx, nu] = Bd.shape
# Constraints
u0 = 10.5916
umin = np.array([9.6, 9.6, 9.6, 9.6]) - u0
umax = np.array([13., 13., 13., 13.]) - u0
xmin = np.array([-np.pi/6,-np.pi/6,-np.inf,-np.inf,-np.inf,-1.,
-np.inf,-np.inf,-np.inf,-np.inf,-np.inf,-np.inf])
xmax = np.array([ np.pi/6, np.pi/6, np.inf, np.inf, np.inf, np.inf,
np.inf, np.inf, np.inf, np.inf, np.inf, np.inf])
# Objective function
Q = sparse.diags([0., 0., 10., 10., 10., 10., 0., 0., 0., 5., 5., 5.])
QN = Q
R = 0.1*sparse.eye(4)
# Initial and reference states
x0 = np.zeros(12)
xr = np.array([0.,0.,1.,0.,0.,0.,0.,0.,0.,0.,0.,0.])
# Prediction horizon
N = 10
# Cast MPC problem to a QP: x = (x(0),x(1),...,x(N),u(0),...,u(N-1))
# - quadratic objective
P = sparse.block_diag([sparse.kron(sparse.eye(N), Q), QN,
sparse.kron(sparse.eye(N), R)], format='csc')
# - linear objective
q = np.hstack([np.kron(np.ones(N), -Q.dot(xr)), -QN.dot(xr),
np.zeros(N*nu)])
# - linear dynamics
Ax = sparse.kron(sparse.eye(N+1),-sparse.eye(nx)) + sparse.kron(sparse.eye(N+1, k=-1), Ad)
Bu = sparse.kron(sparse.vstack([sparse.csc_matrix((1, N)), sparse.eye(N)]), Bd)
Aeq = sparse.hstack([Ax, Bu])
leq = np.hstack([-x0, np.zeros(N*nx)])
ueq = leq
# - input and state constraints
Aineq = sparse.eye((N+1)*nx + N*nu)
lineq = np.hstack([np.kron(np.ones(N+1), xmin), np.kron(np.ones(N), umin)])
uineq = np.hstack([np.kron(np.ones(N+1), xmax), np.kron(np.ones(N), umax)])
# - OSQP constraints
A = sparse.vstack([Aeq, Aineq], format='csc')
l = np.hstack([leq, lineq])
u = np.hstack([ueq, uineq])
# Create an OSQP object
prob = osqp.OSQP()
# Setup workspace
prob.setup(P, q, A, l, u, warm_start=True)
# Simulate in closed loop
ctrl=np.array([0,0,0,0])
while not rospy.is_shutdown():
num=Float64()
num=ctrl[0]
pub.publish(num)
rospy.loginfo("The first element of the u(k) is :%0.6f",num)
rate.sleep()
# Solve
res = prob.solve()
# Check solver status
if res.info.status != 'solved':raise ValueError('OSQP did not solve the problem!')
# Apply first control input to the plant
ctrl = res.x[-N*nu:-(N-1)*nu]
x0 = Ad.dot(x0) + Bd.dot(ctrl)
# Update initial state
l[:nx] = -x0
u[:nx] = -x0
prob.update(l=l, u=u)
if __name__ == '__main__':
try:
publisher()
except rospy.ROSInterruptException:
pass

測試結果如下：

rosrun命令結果：

[email protected]:~$ rosrun path_track mpc.py
-----------------------------------------------------------------
OSQP v0.6.2 - Operator Splitting QP Solver
(c) Bartolomeo Stellato, Goran Banjac
University of Oxford - Stanford University 2021
-----------------------------------------------------------------
problem: variables n = 172, constraints m = 304
nnz(P) + nnz(A) = 1161
settings: linear system solver = qdldl,
eps_abs = 1.0e-03, eps_rel = 1.0e-03,
eps_prim_inf = 1.0e-04, eps_dual_inf = 1.0e-04,
rho = 1.00e-01 (adaptive),
sigma = 1.00e-06, alpha = 1.60, max_iter = 4000
check_termination: on (interval 25),
scaling: on, scaled_termination: off
warm start: on, polish: off, time_limit: off
[INFO] [1643197163.344612]: The first element of the u(k) is :0.000000
iter objective pri res dua res rho time
1 -3.2965e+01 8.15e-01 6.00e+00 1.00e-01 7.91e-04s
25 -4.0983e+01 6.50e-05 2.15e-04 1.00e-01 1.20e-03s
status: solved
number of iterations: 25
optimal objective: -40.9834
run time: 1.24e-03s
optimal rho estimate: 9.40e-02
[INFO] [1643197163.427086]: The first element of the u(k) is :-0.991535
iter objective pri res dua res rho time
1 -4.0983e+01 1.67e+00 9.40e+02 1.00e-01 1.04e-04s
25 -4.6383e+01 4.50e-04 4.45e-03 1.00e-01 5.10e-04s
status: solved
number of iterations: 25
optimal objective: -46.3833
run time: 5.43e-04s
optimal rho estimate: 4.51e-02
[INFO] [1643197163.526112]: The first element of the u(k) is :-0.991686
iter objective pri res dua res rho time
1 -4.6383e+01 9.59e-01 5.39e+02 1.00e-01 9.74e-05s
25 -5.0969e+01 2.47e-04 2.56e-03 1.00e-01 5.11e-04s
status: solved
number of iterations: 25
optimal objective: -50.9693
run time: 5.45e-04s
optimal rho estimate: 4.41e-02
[INFO] [1643197163.625625]: The first element of the u(k) is :-0.425915
iter objective pri res dua res rho time
1 -5.0970e+01 2.76e-01 4.91e+02 1.00e-01 9.35e-05s
25 -5.3505e+01 5.87e-05 2.33e-03 1.00e-01 5.06e-04s
status: solved
number of iterations: 25
optimal objective: -53.5053
run time: 5.39e-04s
optimal rho estimate: 3.74e-02
[INFO] [1643197163.725921]: The first element of the u(k) is :0.750120
iter objective pri res dua res rho time
1 -5.3506e+01 9.31e-01 5.24e+02 1.00e-01 7.27e-05s
25 -5.4539e+01 2.58e-04 2.48e-03 1.00e-01 4.69e-04s
status: solved
number of iterations: 25
optimal objective: -54.5391
run time: 5.04e-04s
optimal rho estimate: 5.56e-02
[INFO] [1643197163.825315]: The first element of the u(k) is :0.829224
iter objective pri res dua res rho time
1 -5.4539e+01 1.01e+00 5.66e+02 1.00e-01 7.17e-05s
25 -5.4854e+01 2.74e-04 2.68e-03 1.00e-01 3.35e-04s
status: solved
number of iterations: 25
optimal objective: -54.8543
run time: 3.56e-04s
optimal rho estimate: 5.69e-02
[INFO] [1643197163.925019]: The first element of the u(k) is :0.560168
^Citer objective pri res dua res rho time
1 -5.4854e+01 6.77e-01 3.81e+02 1.00e-01 1.00e-04s
25 -5.4932e+01 1.83e-04 1.80e-03 1.00e-01 3.27e-04s
status: solved
number of iterations: 25
optimal objective: -54.9324
run time: 3.92e-04s
optimal rho estimate: 5.66e-02
[email protected]:~$

topic訂閱得話題內容如下：

[email protected]:~$ rostopic echo mpc_pub
data: -0.991534988484
---
data: -0.991686079847
---
data: -0.425914685439
---
data: 0.75012029663
---
data: 0.829224461171
---
data: 0.560167648007
---

可以看到所需要的控制變量會按照預測結果逐個輸出。