1.定義:算法是指解題方案的准確而完整的描述。算法是模型分析的一組可行的,確定的和有窮的規則。
2.特征:
a)有窮性(Finiteness):算法必須能在執行有限個步驟之後終止。
b)確切性(Definiteness):算法的每一步驟必須有確切的定義。
c)輸入項(Input):算法有0個或多個輸入,以刻畫運算對象的初始情況。
d)輸出項(Output):算法有一個或多個輸出,以反映對輸入數據加工後的結果。沒有輸出的算法是毫無意義的;
e)可行性(Effectiveness):算法中執行的任何計算步驟都是可以被分解為基本的可執行的操作步,即每個計算步都可以在有限時間內完成(也稱之為有效性)。
3.要素
a)對數據對象的運算和操作: 算術運算、邏輯運算、關系運算、數據傳輸。
b)算法的控制結構:算法的執行順序(順序、選擇、循環)
4.復雜度
a) 時間復雜度:是指執行算法所需要的計算工作量,可以用算法所執行的基本運算次數度量。
b) 空間復雜度:是指執行算法所需要的內存空間。包括算法程序、輸入的初始數據以及算法執行過程中需要的額外空間。
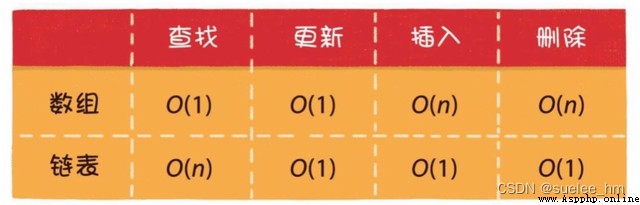
1.數組

基本操作:讀取O(1)、更新O(1)、插入O(n)、刪除O(n)、擴容O(n)。
2.鏈表
單向鏈表的每一個節點又包含兩部分,一部分是存放數據的變量data,另一部分是指向下一個節點的指針next。

基本操作:讀取O(n)、更新O(1)、插入O(1)、刪除O(1)。
數組和鏈表對比
數組:適合多讀、插入刪除少的場景。
鏈表:適用於插入刪除多、讀少的場景
3.棧
棧是一種線性邏輯數據結構,棧的元素只能後進先出。最早進入的元素存放的位置叫做棧底,最後進入的元素存放的位置叫棧頂。棧只能從一端進出。

基本操作:入棧O(1)、出棧O(1)。
4.隊列
隊列是一種線性邏輯數據結構,隊列的元素只能後進後出。隊列的出口端叫做隊頭,隊列的入口端叫做隊尾。一頭進,另一頭出。

基本操作:入隊 O(1)、出隊 O(1)。
5.哈希表
一種邏輯數據結構,提供了鍵(key)和值(value)的映射關系。
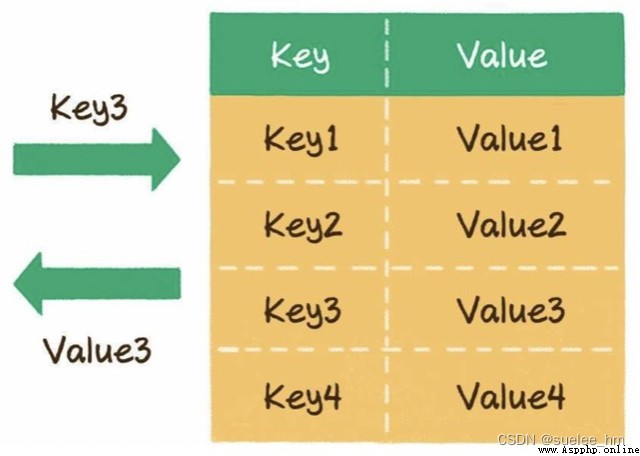
基本操作:寫入:O(1)、讀取:O(1)、擴容O(n)。
6.樹
樹是由根節點和若干顆子樹構成的。樹是由一個集合以及在該集合上定義的一種關系構成的。集合中的元素稱為樹的節點,所定義的關系稱為父子關系。父子關系在樹的節點之間建立了一個層次結構。在這種層次結構中有一個節點具有特殊的地位,這個節點稱為該樹的根節點,或稱為樹根。
簡單的說,算法就是計算機解題的過程。 在這個過程中,無論是形成解題思路還是編寫程序,都是在實施某種算法。前者是算法的邏輯形式,後者是算法的代碼形式。
如:求1+2+3+...998+999+1000=?
算法1:依次相加: 循環處理 ---處理999次
算法2:高斯解法:首尾相加*500 (1+1000)*1000/2 ---處理3次
算法3:使用遞歸實現---處理100次
sum(100) = sum(99)+100
sum(99) = sum(98)+99
.....
sum(2) = sum(1)+2
sum(1) = 1
評價算法優劣的依據:復雜度(時間復雜度和空間復雜度)
計算機資源最重要的是時間和空間資源,因此復雜度分為時間和空間復雜度,時間復雜度是指執行算法所需要的計算工作量,空間復雜度是指執行這個算法所需要的內存空間。
1.時間復雜度(Time Complexity)
一個算法花費的時間與算法中語句的執行次數成正比例,哪個算法中語句執行次數多,它花費時間就多。 一個算法中的語句執行次數稱為語句頻度或時間頻度。
2. 空間復雜度(Space Complexity)
空間復雜度是對一個算法在運行過程中臨時占用存儲空間大小的量度。
算法復雜度分為時間復雜度和空間復雜度。其作用: 時間復雜度是指執行算法所需要的計算工作量;而空間復雜度是指執行這個算法所需要的內存空間。
排序(sorting)的功能是將一個數據元素的任意序列,重新排列成一個按關鍵字有序的序列。

從大量數據中找出需要的數據。
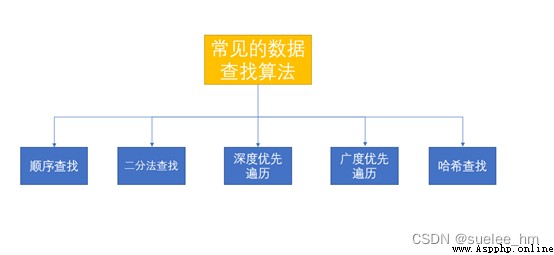
[1]:百度安全驗證