一、引言

一元線性回歸：涉及的變量只有一個

多元線性回歸：涉及的變量兩個或兩個以上

預測結果與真實值是有一定的誤差（如圖）：

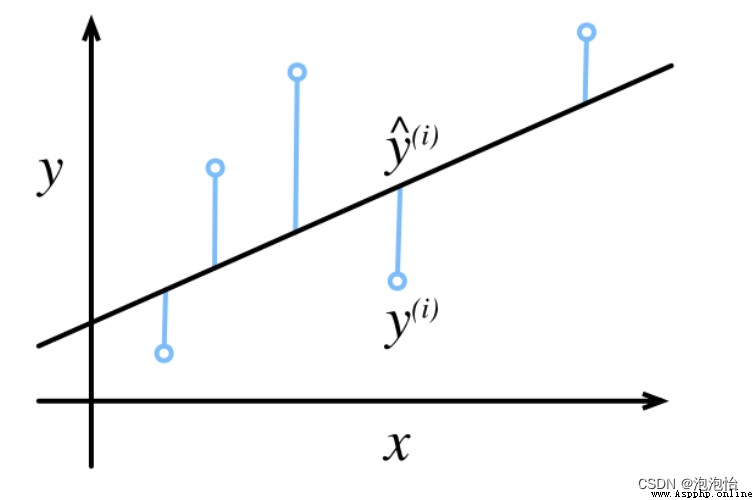
 本文以y=-2x+8的數據進行擬合為例，給出了利用最小二乘法來估計回歸系數的方法及python實現。

二、公式推導

1.最小二乘法：

假設已知一系列的散點（xi,yi)

我們將（xi,yi)代入 y =kx+b 得

 構造最小二乘函數：

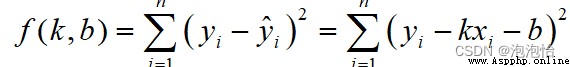
 對k和b分別求偏導數得：

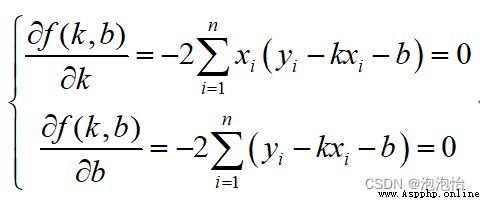
上述方程組兩端同時除以n得：

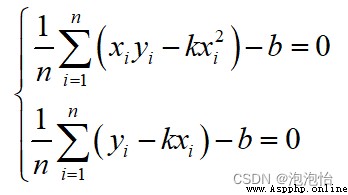
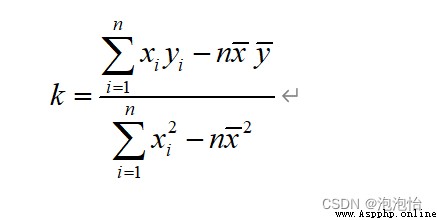
 將其代入即可得到系數b。

 三、python程序

1.根據散點圖判讀曲線變化趨勢

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trainX=np.arange(25)
trainY=2*trainX+8+np.random.randn(25)
plt.scatter(trainX, trainY,color='red',marker='+')

結果如圖所示：

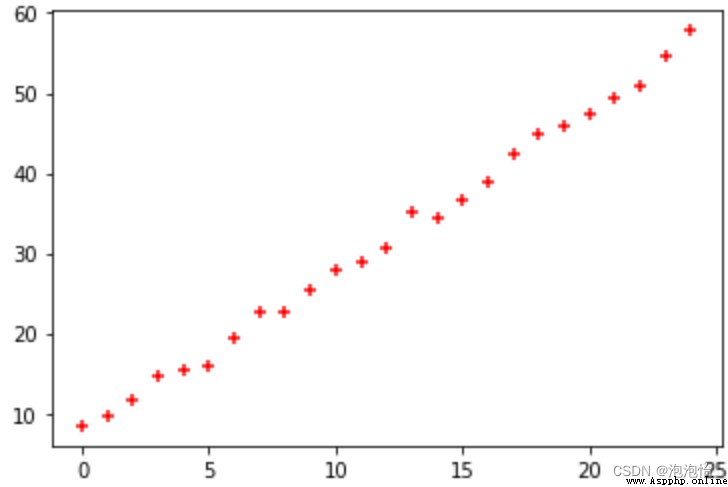
2.回歸系數計算如下：

n=25
xu=np.sum(trainX)/n
yu=np.sum(trainY)/n
k1 = sum( trainX * trainY ) - n * xu * yu;
k2 = sum( trainX * trainX ) - n * xu * xu;
k = k1 / k2;
b = yu - k * xu;

 結果如下：k=2.0174825107892924, b=7.508028732222016

3.完整代碼如下

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trainX=np.arange(25)
trainY=2*trainX+8+np.random.randn(25)
plt.scatter(trainX, trainY,color='red',marker='+')
n=25
xu=np.sum(trainX)/n
yu=np.sum(trainY)/n
k1 = sum( trainX * trainY ) - n * xu * yu;
k2 = sum( trainX * trainX ) - n * xu * xu;
k = k1 / k2;
b = yu - k * xu;
Y1=k*trainX+b
fig,ax = plt.subplots()
ax.scatter(trainX, trainY,color='red',marker='+')
ax.plot(trainX, Y1,color='blue')

 結果如圖：

注意：附加最大似然估計的推導：