一.前言

       這篇主要是用神經網絡來預測手寫數據集，用的數據還是多分類邏輯回歸的數據，這次多填了一個ex3weight.mat文件，有5000個樣本，400列特征值

二.代碼解析

1.導入包

        這裡的包和多分類邏輯回歸中所用到的相同

import numpy as np
import matplotlib.pyplot as plt
from scipy.io import loadmat

2.數據導入與數據初始化

        這裡需要取倆個文件，ex3data1中存放的是X，y為鍵的數據集，ex3weights中存放的是倆個theta矩陣，分別是用來在第一層和第二層進化數據，這裡同樣需要在X的第一列插入1

data = loadmat('ex3data1.mat')
# print(data) # 查看數據
# print(data.keys()) # 關鍵字(['__header__', '__version__', '__globals__', 'X', 'y'])
data_theta = loadmat('ex3weights.mat') # 存放theta矩陣
# print(data_theta) # 查看一下數據
# print(data.keys()) # 查看關鍵字(['__header__', '__version__', '__globals__', 'Theta1', 'Theta2'])
X = data['X']
y = data['y']
X_add1 = np.matrix(np.insert(X, 0, values=np.ones(5000), axis=1)) # 插入1
y = np.matrix(y)
# print(X_add1.shape,y.shape) # 查看X_add1,y維度---(5000, 401) (5000, 1)
theta1 = np.matrix(data_theta['Theta1'])
theta2 = np.matrix(data_theta['Theta2'])
# print(theta1.shape,theta2.shape) # 查看theta1,theta2維度()---(25, 401) (10, 26)

ex3weights數據展示 

 第一行分別是x_add1和y的維度，第二行是theta1和theta2的維度

 3.sigmoid函數

        這裡不在解釋了，幾乎每一次都要用到

def sigmoid(z):
return 1/(1+np.exp(-z))

4.進行傳遞

        這裡我把傳遞的過程簡單畫了一下，如果看不懂可以結合著老師的視頻看，下面也寫出了在傳遞過程中每一次矩陣維度的變化，分成了三層，每一層都有自己的進化方向，最後一層獲得10個概率值，分別是1-10的預測率hx（圖中忘畫了一個a0,第二層也需要加入一列1）

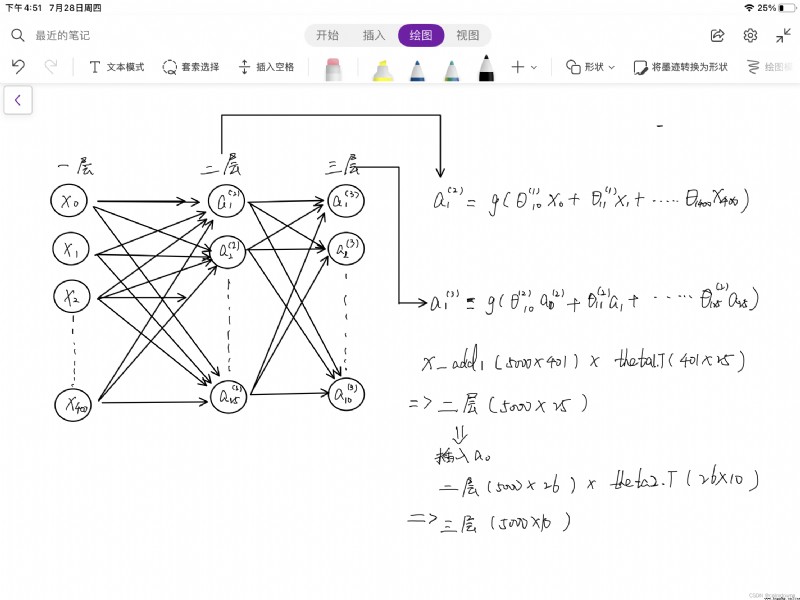
a1 = X_add1 # 第一層（5000*400）
z2 = a1 @ theta1.T
a2 = sigmoid(z2) # 得到第二層矩陣（5000*25）
a2 = np.insert(a2, 0, values=1, axis=1) # 在第二層插入一列1(5000*26)
# print(a2.shape) # (5000, 26)
z3 = a2 @ theta2.T
a3 = sigmoid(z3) # 得到第三層矩陣（5000*10）

5.預測函數

        預測函數和多元邏輯回歸裡的大致相同，這次我們直接獲得了結果矩陣，只需要從5000*10的矩陣中找出每一行最大的hx，並與y進行比較即可，變得更為方便了

# 預測函數
def predict_fuc(a3,y):
p_max = np.argmax(a3,axis=1) # 從a3矩陣中找到每一行中最大值的坐標
p_max_last = np.matrix(p_max.reshape(5000,1) + 1) # 因為返回的下標是0-9所以這裡加一才能與y做對比
count = 0
for i in range(0,5000):
if p_max_last[i] == y[i]:
count += 1
return count/len(y)
pass

6.結果展示 

        可以看到成功率與多分類邏輯回歸相比，提高了很多，運行速度也是快了很多倍，所以神經網絡方法還是很實用的

print(f'預測的成功率為{predict_fuc(a3,y) * 100}%')

 三.全部代碼

import numpy as np
import matplotlib.pyplot as plt
from scipy.io import loadmat
data = loadmat('ex3data1.mat')
# print(data) # 查看數據
# print(data.keys()) # 關鍵字(['__header__', '__version__', '__globals__', 'X', 'y'])
data_theta = loadmat('ex3weights.mat') # 存放theta矩陣
# print(data_theta) # 查看一下數據
# print(data.keys()) # 查看關鍵字(['__header__', '__version__', '__globals__', 'Theta1', 'Theta2'])
X = data['X']
y = data['y']
X_add1 = np.matrix(np.insert(X, 0, values=np.ones(5000), axis=1)) # 插入1
y = np.matrix(y)
# print(X_add1.shape,y.shape) # 查看X_add1,y維度---(5000, 401) (5000, 1)
theta1 = np.matrix(data_theta['Theta1'])
theta2 = np.matrix(data_theta['Theta2'])
# print(theta1.shape,theta2.shape) # 查看theta1,theta2維度()---(25, 401) (10, 26)
def sigmoid(z):
return 1/(1+np.exp(-z))
# 預測函數
def predict_fuc(a3,y):
p_max = np.argmax(a3,axis=1) # 從a3矩陣中找到每一行中最大值的坐標
p_max_last = np.matrix(p_max.reshape(5000,1) + 1) # 因為返回的下標是0-9所以這裡加一才能與y做對比
count = 0
for i in range(0,5000):
if p_max_last[i] == y[i]:
count += 1
return count/len(y)
pass
a1 = X_add1 # 第一層（5000*400）
z2 = a1 @ theta1.T
a2 = sigmoid(z2) # 得到第二層矩陣（5000*25）
a2 = np.insert(a2, 0, values=1, axis=1) # 在第二層插入一列1(5000*26)
# print(a2.shape) # (5000, 26)
z3 = a2 @ theta2.T
a3 = sigmoid(z3) # 得到第三層矩陣（5000*10）
print(f'預測的成功率為{predict_fuc(a3,y) * 100}%')