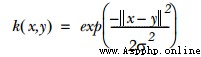本篇內容講一下業界鼎鼎大名的支持向量機,該算法之所以出名,一是模型參數少,稍微調整下,可以直接拿來使用;二是其具有扎實的數學理論基礎支撐;三是模型效果還不錯。因此受到各位大神的喜好,可以說在深度學習出現之前,是最好的機器學習方法之一。
1、支撐向量機的概念
支持向量機(support vector machine,SVM),可以拆開兩部分來看,一是支撐向量,顧名思義,就是支撐構建分類器的向量;二是機,就是機器的意思,也就是分類器的意思,從一個簡單示例來理解其含義和涉及到的術語。
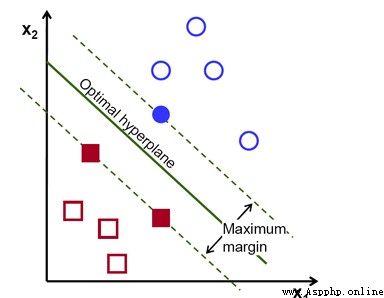
在該圖中,藍色的圈和紅色的塊是要區分的兩個類別,中間的分割直線是分類函數,實心的點就是支持向量,這也是算法的由來。而分類函數就是需要通過模型來尋找的,但這裡有很多分類函數能夠區分,因此需要找一個最穩定和最優化的分類器,該分類器能夠其到達分類邊界最大,就是支撐向量到達分類器最大。
這是線性可分的情況,那什麼是線性可分函數?在一維空間是一個點,二維空間是一條直線,三維空間是一個平面,而在四維及以上,就超出了想象,可統稱為超平面。
但一般我們會遇到非線性情況,因此SVM的方法就是通過一個核函數將低維度數據映射到高維度空間,從而將非線性問題轉換為線性問題。如圖所示,通過數據映射,可以明顯看到有條直線可以將其區分。
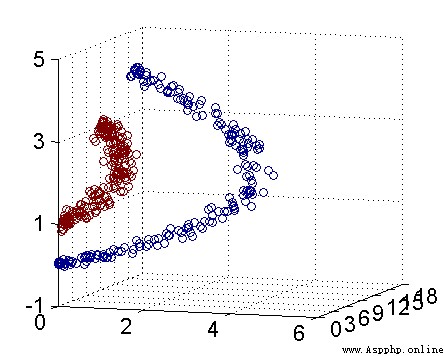
另外,核函數的價值雖然將特征從低維映射到高維空間,但其最牛的地方在於通過在低維空間的計算,能夠實現高維空間的分類,從而避免了維度災難,因此減少了計算量。
2、支撐向量機的特點
如下圖,X是牛群,點是狼群,如何在他們之間建設合適的籬笆?這也是一個二分類問題。下圖就是SVM、邏輯回歸和決策樹構建模型結果。可以看出SVM的分類比較符合實際用途,這就是非線性分類的優勢。
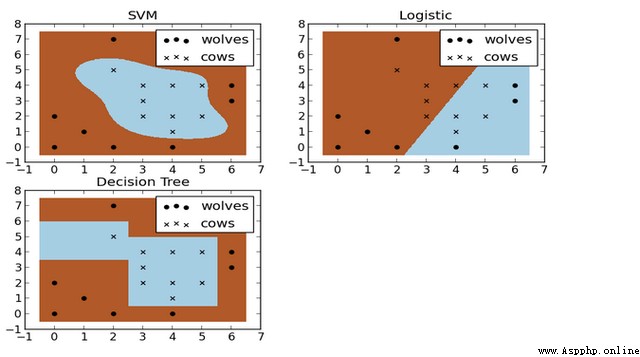
SVM的優點是計算量少,效果好;但其缺點是對參數調節和核函數選擇比較敏感。
3、支撐向量機的推導
關於支撐向量機的推導,網上有很多較好的資料,都講的比較清楚和透徹,如《支持向量機通俗導論(理解SVM的三層境界)》,也有視頻可以看。所以這裡不再過多介紹。但還是幾點學習心得僅供參考。
(1)支撐向量機的核心就是尋找能夠使區間間隔最大化的分類器;
(2)使用拉格朗日乘子法和KKT條件,將其轉化成在約束條件的優化問題,
(3)僅使用支撐向量來對未知樣本進行預測;
(4)通過核函數將數據映射到高維空間,轉化為線性可分;
(5)需要自己設定參數C和K,其中C為松弛變量,用來平衡懲罰誤差,值越大越不能有誤差;K是核函數的參數,決定了映射到高維空間的分布。
以下文章是從網絡整理過來,僅供參考。

4、SMO求解
從SVM的公式推導中,可以看出只要求出alpha,就可求解出w和b,需要的超平面就可得出。而求alpha的方法,目前比較流行的是使用SMO算法,即序列最小優化算法。
其中SMO算法的工作原理是:首先選擇兩個alpha進行優化處理,固定其他alpha;一旦找到合適的alpha,那麼就增大其中一個減少另一個。因為所有alpha的和為0。
其中SMO的求解步驟為(偽代碼):
(1)初始化化alpha,將其設定為0向量;
(2)設定最大的迭代次數(外循環),當迭代次數<最大迭代次數:
(3)對數據集中的每個數據向量(內循環)
:(4)如果該數據向量可以被優化(>設定的最小誤差):
(5)隨機選擇另外一個數據向量:
(6) 同時優化選擇的兩個向量:
(7) 如果兩個向量都不能被優化,退出內循環
(8)如果所有向量都沒被優化,增加迭代數目,繼續下一次循環
因為所選擇的的是隨機向量,因此需要多次迭代,一直到alpha不會在優化為止。
該算法的簡單版本Python代碼如下:
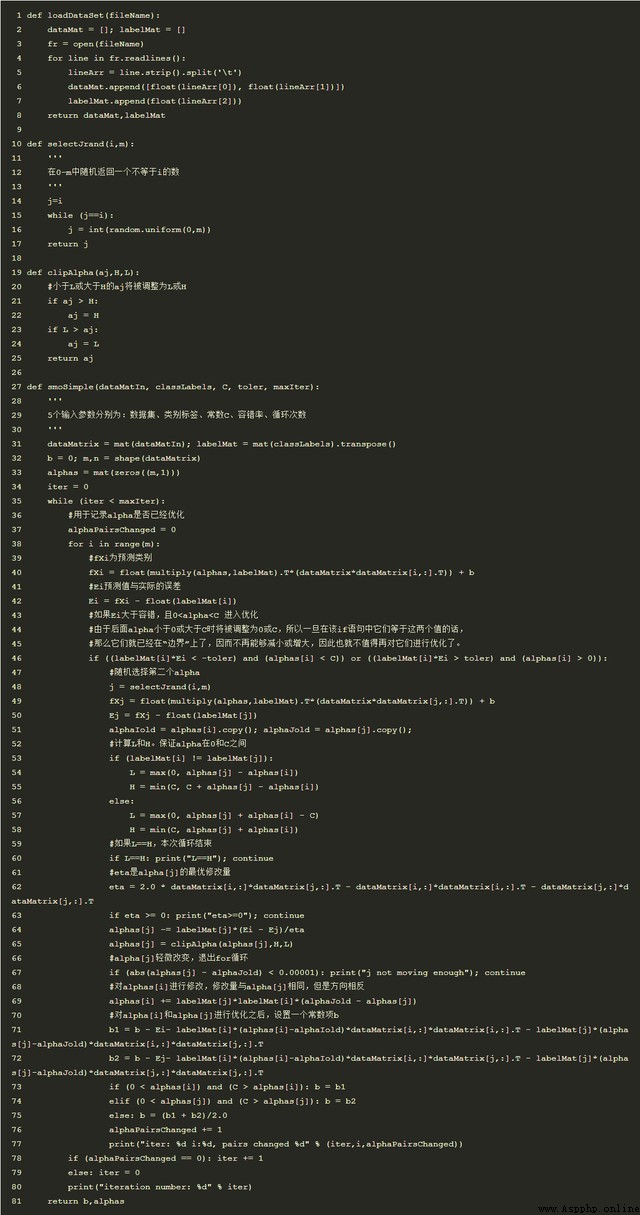
對樣本測試結果:
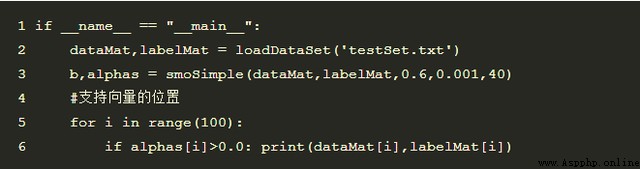
輸出結果為,表示支撐向量共4個,其中正樣本1個,負樣本3:
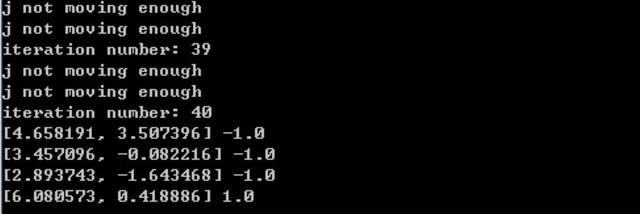
另外,為加快計算速度,在該簡化版本上做了優化處理,該方法為
Platt SMO,從外循環和內循環分別選擇兩個alpha值,快速收斂。
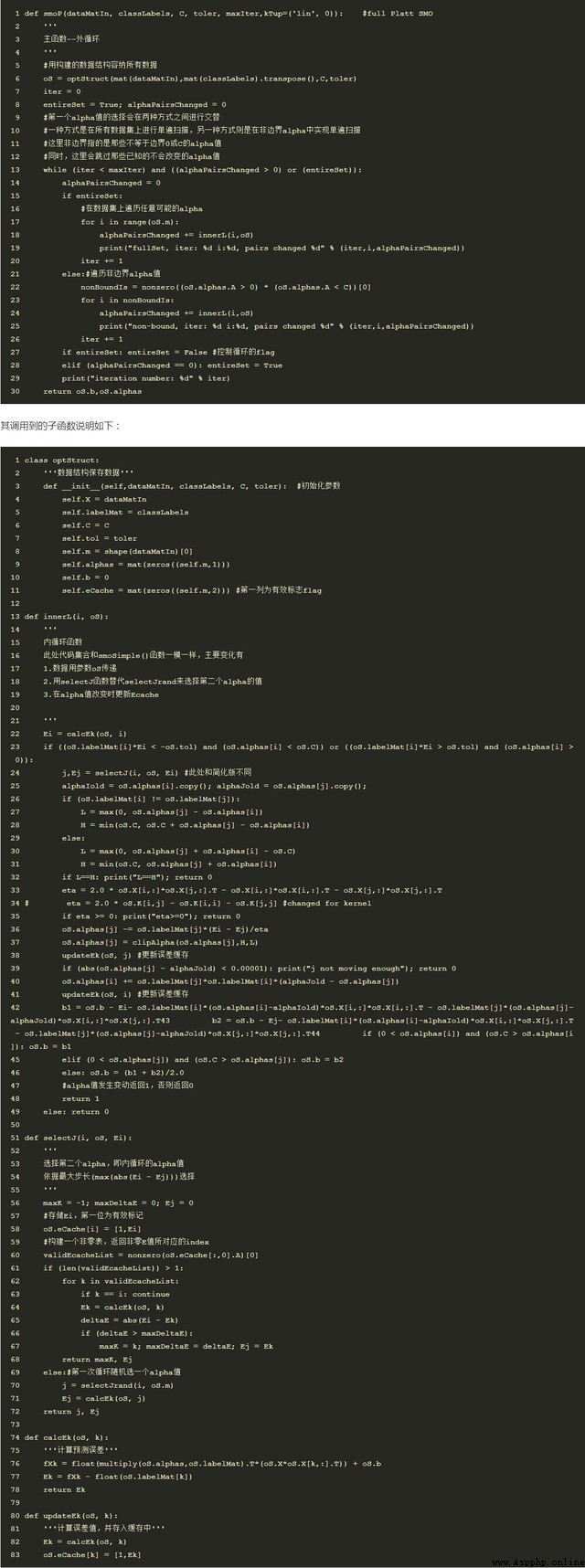
另外,通過計算alpha,可求解w,因此可求解出y=w*x+b來確定超平面;具體代碼如下:
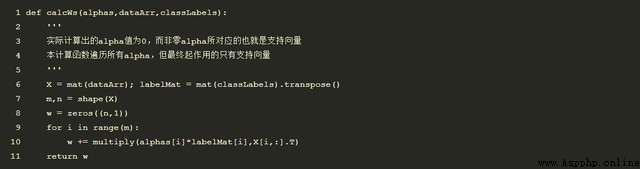
計算示例如下,>0表示類別1,<0表示類別-1:
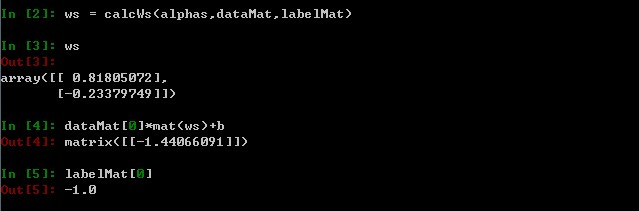
5、支持向量機的核函數
上節講到的只能夠解決線性問題,而對於下圖情況,則效果不好。這時候就需要利用核函數。直觀上講下圖就是兩個圓,因此如果映射到三維空間就可以通過一個平面區分。如通過將(x,y)映射為(x,y,x^2+y^2)
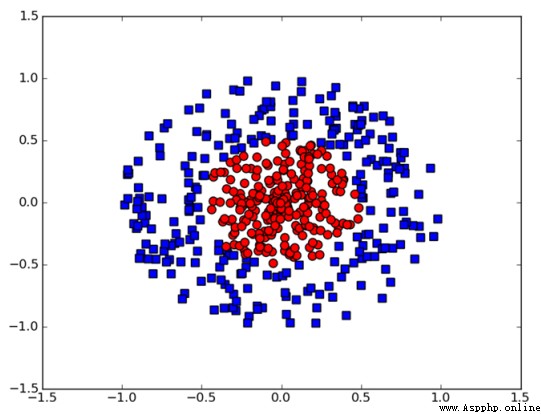
一般使用的是高斯徑向基函數
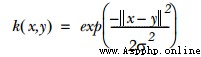
其中sigam是計算收斂速度的參數,也是需要調整優化的參數。其中相關代碼如下
KernelTrans():函數是用來向量的轉化。
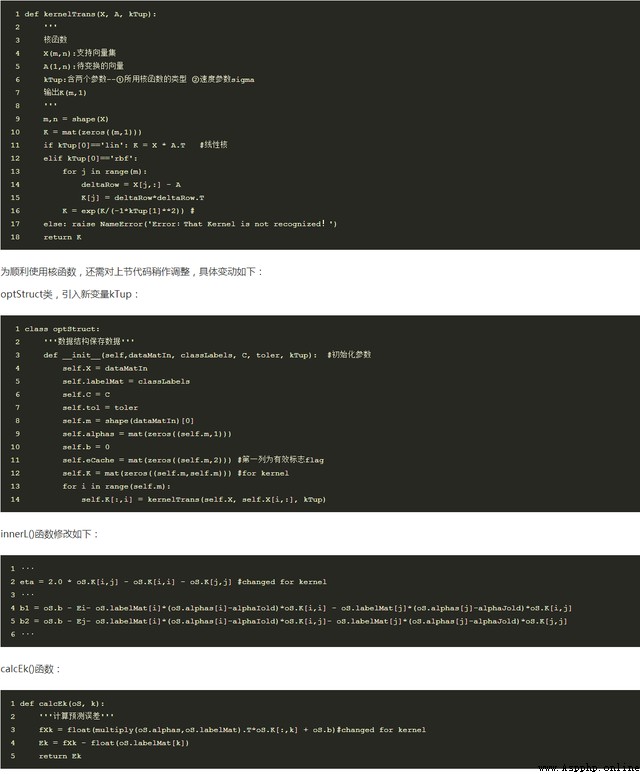
6、Python實現示例
本次使用的例子是手寫識別樣本,包括兩類樣本,其中0設為1,9設為-1.該方法的優勢在於僅需要保存支持向量機就可以進行預測。
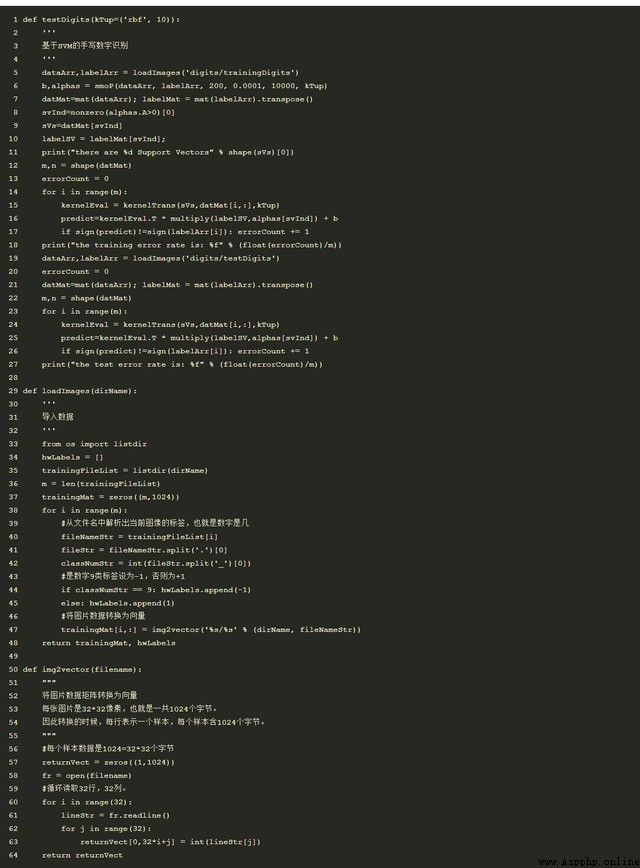
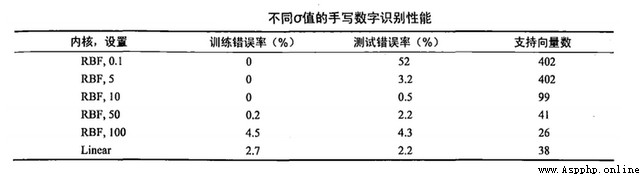
結果如下,本次選擇的參數為C=200,sigma=10
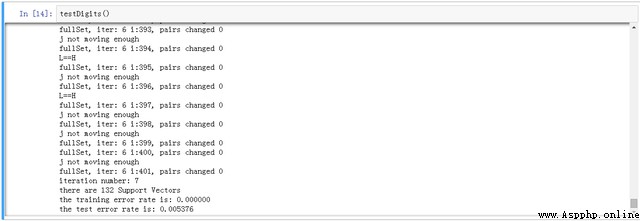
另外,C和k值等參數取值不同,導致的預測結果和支撐向量也各異,也說明了該方法對參數調整比較敏感。還對比了線性模型,核函數結果較優。