Welcome to
Personal home page ： Power System Research Office
Column catalog ： The beauty of power system and algorithm
【 Now the name of official account is changed to ： Litchi Scientific Research Society 】
Bloggers' extracurricular interests ： Chinese and Western Philosophy , To readers ：
Do research , It involves a deep ideological system , Researchers need to be logical , Be practical and serious , But you can't just try , Many times, borrowing is more important than trying , Then there should be innovation and inspiration to look up to the stars . In this column, I will record some philosophical thinking and scientific research notes when I am free ： Scientific research and philosophy . Readers are advised to browse one by one in the order of the catalogue , Lest you suddenly fall into the dark maze and can't find the way to come , It's not enough to reveal the answers to all your questions , But if you can raise doubts in your chest , It may not lead to a different scene with beautiful sunset , If it actually brings you a bitter rain in the spiritual world , Then take the opportunity to wash the things that were stored there “ truth ” Dust on the .
Maybe , After the rain, the clouds gather , God Chi's heaven and earth is more clear .......
The contents of this article are as follows ：️️️
Catalog
1 Knowledge point
1.1 Ant colony algorithm steps
1.2 Ant colony algorithm program
2 Ant algorithm to solve the shortest path problem ——Python Realization
2.1 The source code to achieve
2.2 ACA_TSP Realization
3 Ant algorithm to solve the shortest path problem ——Matlab Realization
4 Ant algorithm solves quadratic assignment problem ——Matlab Realization
5 Ant algorithm solves knapsack problem ——Matlab Realization
6 Improved ant algorithm ——BP Neural network Ant Optimization Algorithm
7 At the end
For details, see ： Intelligent optimization algorithm — Ant colony algorithm （Python Realization ）
In this section, we only talk about Ant colony algorithm to solve the shortest path steps and processes .
1.1 Ant colony algorithm steps
Let the number of ants be m, The number of locations is n, place i And location j Distance between Dij,t Time and place i And location j The pheromone concentration on the connected path is Sij, At the initial time, the pheromone concentration on the path between each location is equal .
Ant k The next target location is determined according to the pheromone on the connection path between each location ,Pijk Express t Time ants k From place i The probability of transfer , The probability calculation formula is as follows ：
In the above formula ,
For the heuristic function ,
, Indicates where the ants are from i Move to location j The degree of expectation ;
For the ants k A collection of places to visit , At the beginning of the
Ants release pheromones at the same time , The pheromone on the connection path between each location gradually disappears , With the parameters
Indicates the volatilization degree of pheromone . therefore , When all the ants complete a cycle , The pheromone concentration on the connection path between each location needs to be updated , That is, ants pass by and leave pheromones , There is a formula expressed as ：
among ,
It means the first one k An ant is in the spot i And j Pheromone concentration released on the connection path ;
1.2 Ant colony algorithm program
(1) Parameter initialization
Looking for the shortest money , All parameters of the program need to be initialized , Ant colony size m、 Pheromone importance factor α、 Heuristic function importance factor β、 Pheromone hair factor 、 Maximum number of iterations ddcs_max, The initial iteration value is ddcs=1.
(2) Construct solution space
Place each ant randomly at a different starting point , Calculate the location of the next visit according to the formula , Until all the ants have visited all the places .
(3) Update pheromones
Calculate the total length of each ant's path Lk, Record the best path in the current cycle , At the same time, the pheromone concentration on the connection path between each location is updated according to the formula .
(4) Termination judgment
Before the number of iterations reaches the maximum , Clear the record of ants passing , And go back to step (2).
Intelligent optimization algorithm — Ant colony algorithm （Python Realization ）
Supplementary information ：scipy.spatial.distance.cdist
#============ Import related libraries =================
import numpy as np
from scipy import spatial
import pandas as pd
import matplotlib.pyplot as plt
from sko.ACA import ACA_TSP
num_points = 25
points_coordinate = np.random.rand(num_points, 2) # Generate the coordinates of the point
distance_matrix = spatial.distance.cdist(points_coordinate, points_coordinate, metric='euclidean')# The function is used to calculate the distance between two input sets
def cal_total_distance(routine):
num_points, = routine.shape
return sum([distance_matrix[routine[i % num_points], routine[(i + 1) % num_points]] for i in range(num_points)])
#=============ACA_TSP solve ==================================
aca = ACA_TSP(func=cal_total_distance, n_dim=num_points,
size_pop=50, max_iter=200,
distance_matrix=distance_matrix)
best_x, best_y = aca.run()
#============= visualization =======================
fig, ax = plt.subplots(1, 2)
best_points_ = np.concatenate([best_x, [best_x[0]]])
best_points_coordinate = points_coordinate[best_points_, :]
ax[0].plot(best_points_coordinate[:, 0], best_points_coordinate[:, 1], 'o-r')
pd.DataFrame(aca.y_best_history).cummin().plot(ax=ax[1])
plt.show()
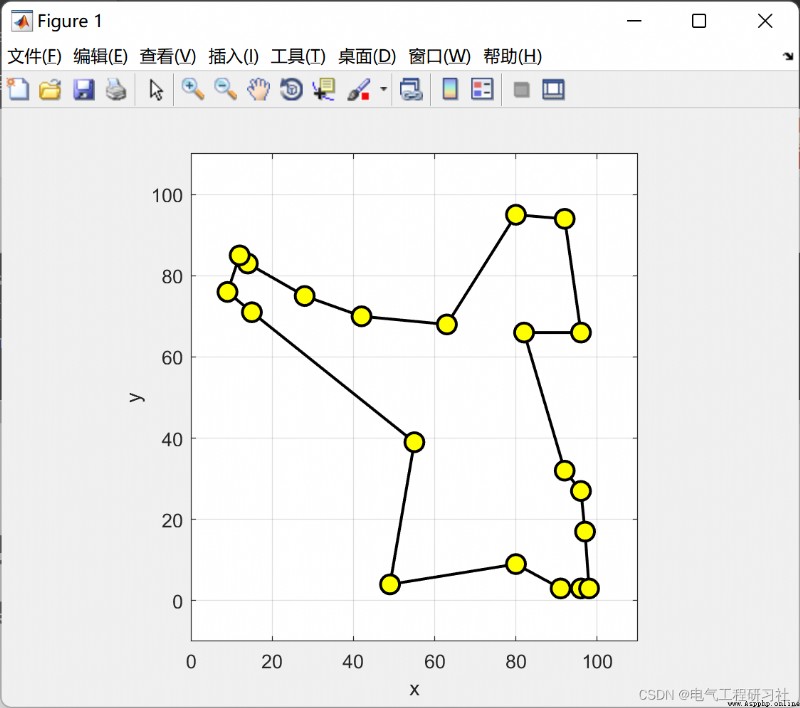
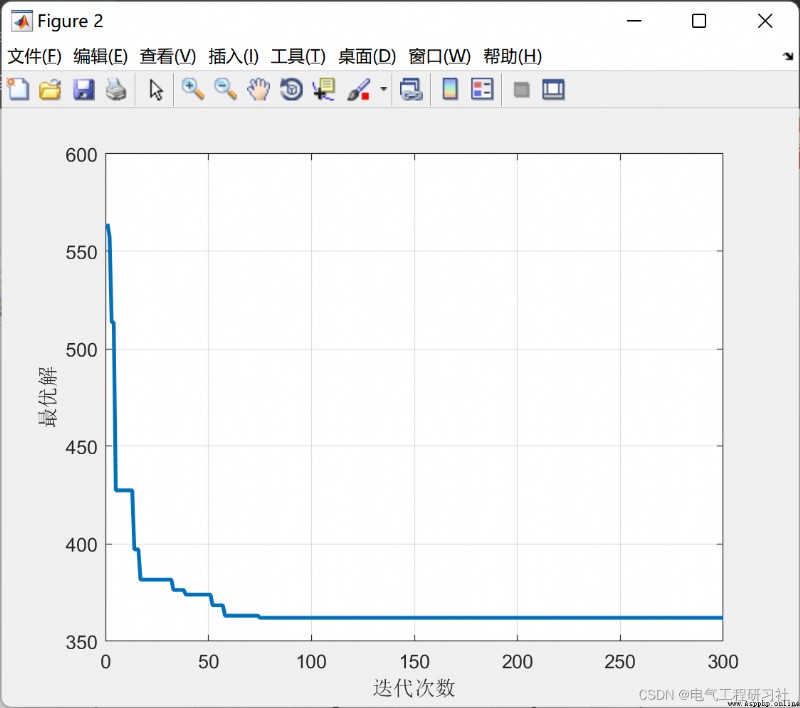
The complete code is here ： Ant algorithm solves the shortest path
In social network analysis , There is a way to study the relationship between relationships , Popular speaking , Is to study the correlation and regression of two matrices . This method is called QAP(Quadratic Assignment Procedure, Secondary assignment procedure ). It compares the similarity of the lattice values of the two matrices , Give the correlation coefficient between the two matrices , At the same time, the coefficient is tested nonparametric , It is based on the replacement of matrix data .
QAP The difference from other standard statistical procedures is , The values of the matrix are not independent of each other , Therefore, parameter estimation and statistical test cannot be carried out with many standard statistical procedures , Otherwise, the accountant calculates the wrong standard deviation . For this question , Scholars use a randomized test （randomization test） To test ,QAP Belong to one of them .
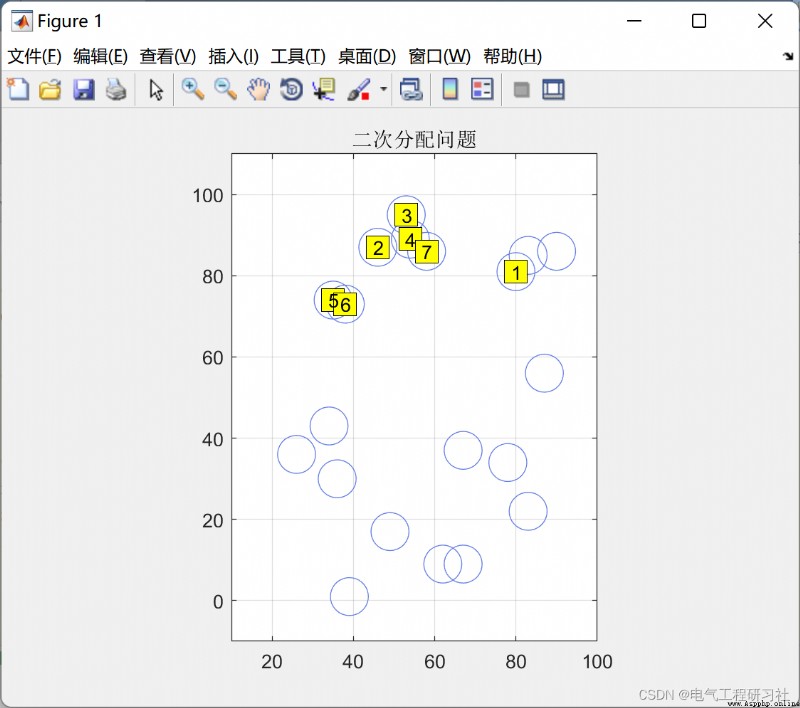
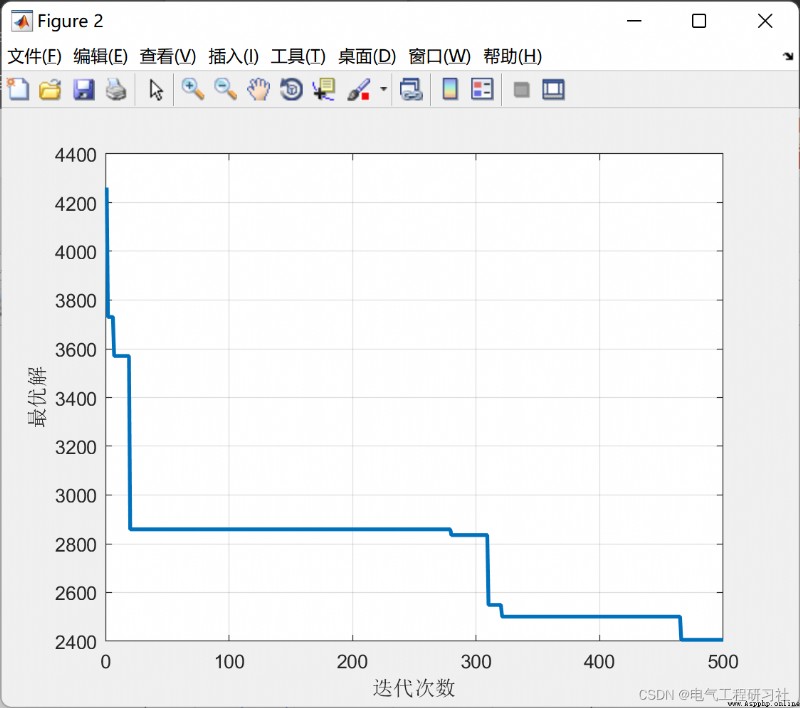
The complete code needs to click here ： Ant algorithm solves quadratic assignment problem
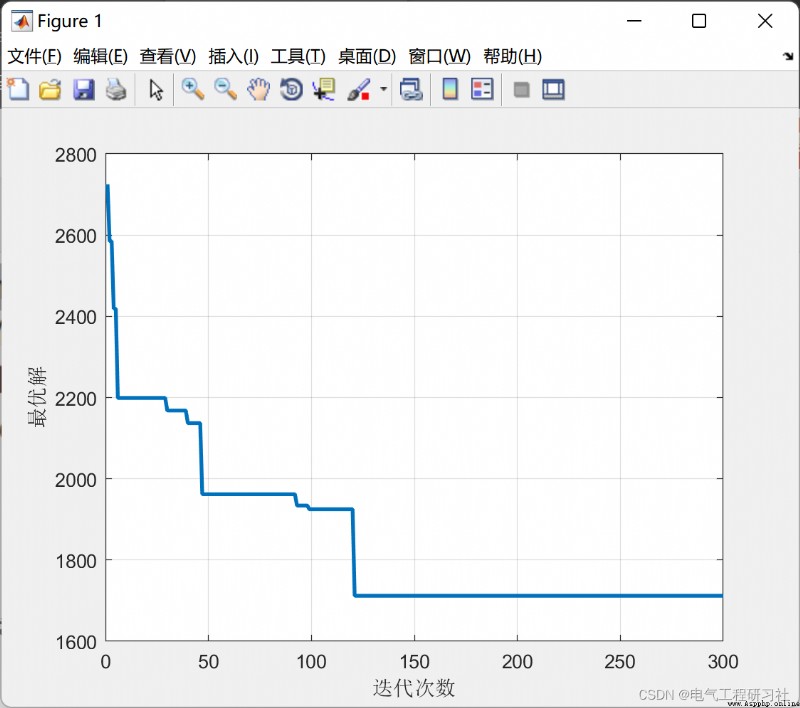
The complete code is here ： Ant algorithm solves knapsack problem
Improved a little , If you are interested, you can have a look at , You may also need your own processing ：BP Neural network Ant Optimization Algorithm
Some theories cite network literature , If there is infringement, please contact the blogger to delete .
