歡迎您的到來
個人主頁：電力系統科研室
專欄目錄：電力系統與算法之美
【現在公眾號名字改為：荔枝科研社】
博主課外興趣：中西方哲學，送予讀者：
做科研，涉及到一個深在的思想系統，需要科研者邏輯缜密，踏實認真，但是不能只是努力，很多時候借力比努力更重要，然後還要有仰望星空的創新點和啟發點。在我這個專欄記錄我有空時的一些哲學思考和科研筆記：科研和哲思。建議讀者按目錄次序逐一浏覽，免得驟然跌入幽暗的迷宮找不到來時的路，它不足為你揭示全部問題的答案，但若能讓人胸中升起一朵朵疑雲，也未嘗不會釀成晚霞斑斓的別一番景致，萬一它居然給你帶來了一場精神世界的苦雨，那就借機洗刷一下原來存放在那兒的“真理”上的塵埃吧。
或許，雨過雲收，神馳的天地更清朗.......
本文目錄如下：️️️
目錄
1 知識點
1.1 蟻群算法步驟
1.2 蟻群算法程序
2 螞蟻算法求解最短路徑問題——Python實現
2.1 源碼實現
2.2 ACA_TSP實現
3 螞蟻算法求解最短路徑問題——Matlab實現
4 螞蟻算法求解二次指派問題——Matlab實現
5 螞蟻算法求解背包問題——Matlab實現
6 改進螞蟻算法——BP神經網絡螞蟻優化算法
7 寫在最後
詳細知識點見：智能優化算法—蟻群算法（Python實現）
我們這一節知識點只講蟻群算法求解最短路徑步驟及流程。
1.1 蟻群算法步驟
設螞蟻的數量為m，地點的數量為n，地點i與地點j之間相距Dij，t時刻地點i與地點j連接的路徑上的信息素濃度為Sij,初始時刻每個地點間路徑上的信息素濃度相等。
螞蟻k根據各個地點間連接路徑上的信息素決定下一個目標地點，Pijk表示t時刻螞蟻k從地點i轉移的概率，概率計算公式如下：
上式中，
為啟發函數，
，表示螞蟻從地點i轉移到地點j的期望程度；
為螞蟻k即將訪問地點的集合，開始時
螞蟻在釋放信息素的同時，每個地點間連接路徑上的信息素逐漸消失，用參數
表示信息素的揮發程度。因此，當所有螞蟻完成一次循環後，每個地點間連接路徑上的信息素濃度需更新，也就是有螞蟻路過並且留下信息素，有公式表示為：
其中，
表示第k只螞蟻在地點i與j連接路徑上釋放的信息素濃度；
1.2 蟻群算法程序
(1)參數初始化
在尋最短路錢，需對程序各個參數進行初始化，蟻群規模m、信息素重要程度因子α、啟發函數重要程度因子β、信息素會發因子、最大迭代次數ddcs_max，初始迭代值為ddcs=1。
(2)構建解空間
將每只螞蟻隨機放置在不同的出發地點，對螞蟻訪問行為按照公式計算下一個訪問的地點，直到所有螞蟻訪問完所有地點。
(3)更新信息素
計算每只螞蟻經過的路徑總長Lk,記錄當前循環中的最優路徑，同時根據公式對各個地點間連接路徑上的信息素濃度進行更新。
(4)判斷終止
迭代次數達到最大值前，清空螞蟻經過的記錄，並返回步驟(2)。
智能優化算法—蟻群算法（Python實現）
補充知識點：scipy.spatial.distance.cdist
#============導入相關庫=================
import numpy as np
from scipy import spatial
import pandas as pd
import matplotlib.pyplot as plt
from sko.ACA import ACA_TSP
num_points = 25
points_coordinate = np.random.rand(num_points, 2) # 生成點的坐標
distance_matrix = spatial.distance.cdist(points_coordinate, points_coordinate, metric='euclidean')#函數用於計算兩個輸入集合的距離
def cal_total_distance(routine):
num_points, = routine.shape
return sum([distance_matrix[routine[i % num_points], routine[(i + 1) % num_points]] for i in range(num_points)])
#=============ACA_TSP解決==================================
aca = ACA_TSP(func=cal_total_distance, n_dim=num_points,
size_pop=50, max_iter=200,
distance_matrix=distance_matrix)
best_x, best_y = aca.run()
#=============可視化=======================
fig, ax = plt.subplots(1, 2)
best_points_ = np.concatenate([best_x, [best_x[0]]])
best_points_coordinate = points_coordinate[best_points_, :]
ax[0].plot(best_points_coordinate[:, 0], best_points_coordinate[:, 1], 'o-r')
pd.DataFrame(aca.y_best_history).cummin().plot(ax=ax[1])
plt.show()
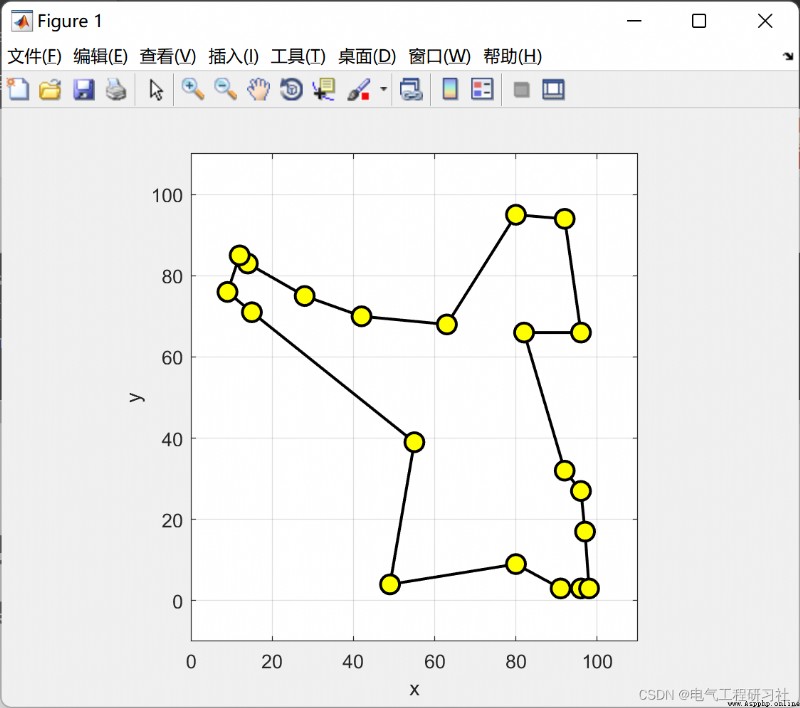
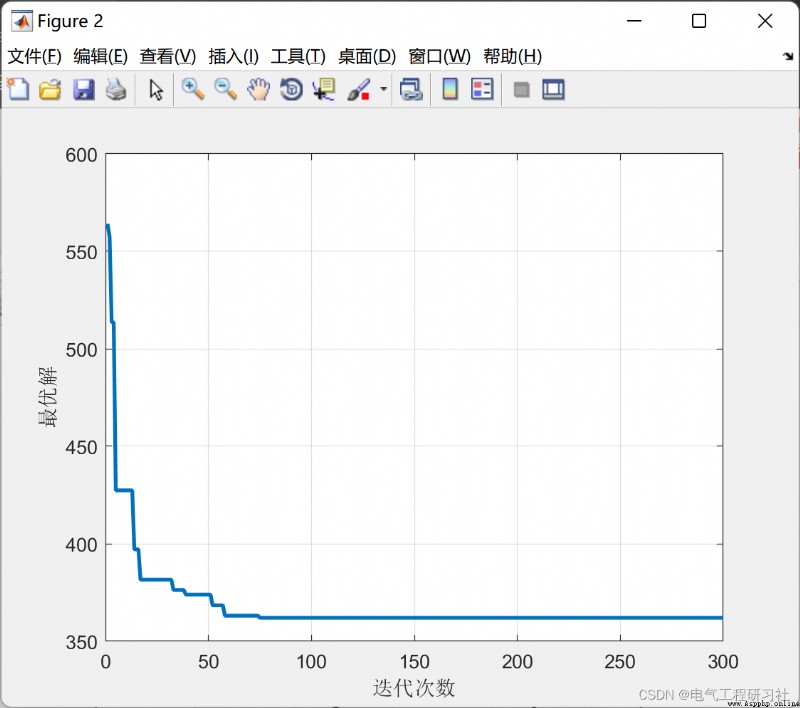
完整代碼點這裡： 螞蟻算法求解最短路徑
在社會網絡分析中，有一種方法用來研究關系之間的關系，通俗來講，就是研究兩個方陣的相關性和回歸性。這種方法叫做QAP(Quadratic Assignment Procedure，二次指派程序)。它對兩個方陣各個格值的相似性進行比較，給出兩個矩陣之間的相關系數，同時對系數進行非參數檢驗，它以對矩陣數據的置換為基礎。
QAP與其他標准的統計程序的不同之處在於，矩陣的各個值之間不相互獨立，因此用許多標准的統計程序就不能對其進行參數估計和統計檢驗，否則會計算出錯誤的標准差。對於這個問題，學者們利用一種隨機化檢驗方法（randomization test）來檢驗，QAP屬於其中一種。
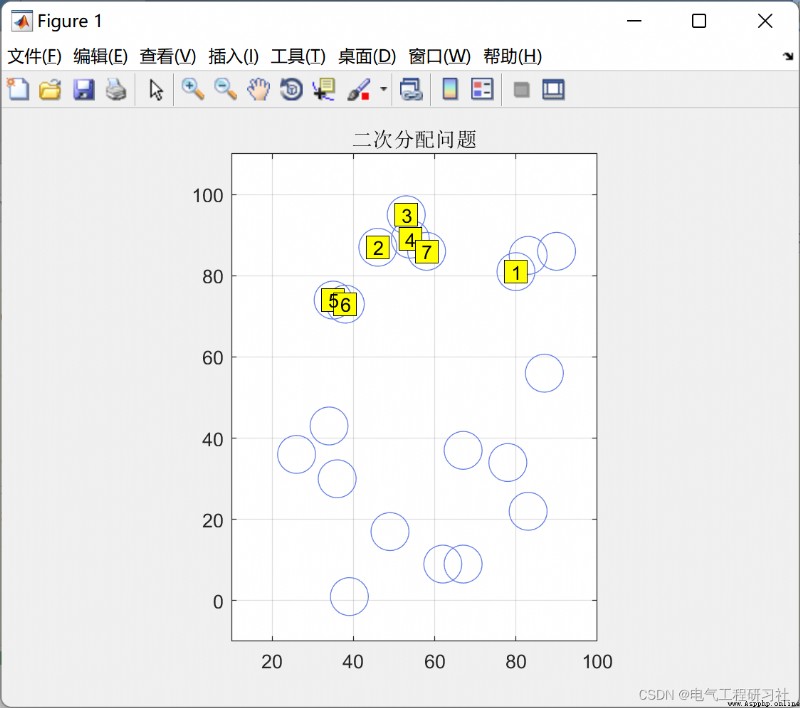
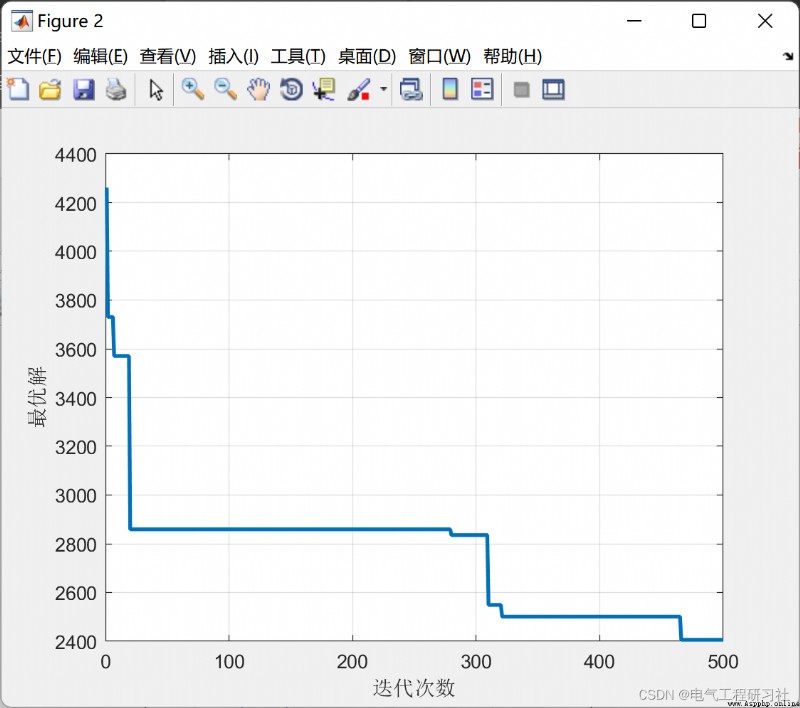
完整代碼需要點這裡： 螞蟻算法求解二次指派問題
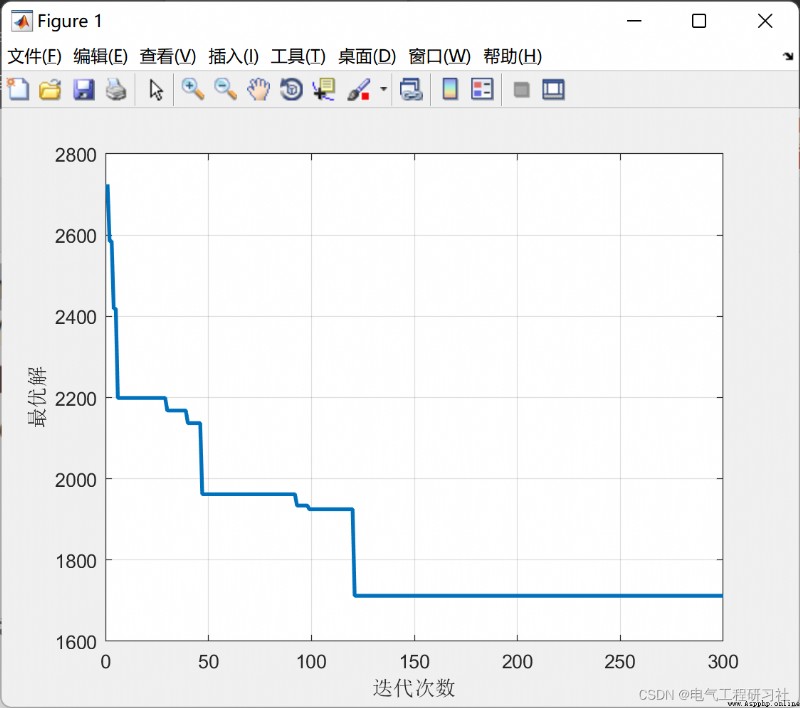
完整代碼點這裡：螞蟻算法求解背包問題
改進了少許，感興趣可以看看，可能還需要你自己的加工：BP神經網絡螞蟻優化算法
部分理論引用網絡文獻，若有侵權請聯系博主刪除。
