您现在的位置：程式師世界 >> 編程語言 > >> 更多編程語言 >> Python

Python數據結構（第1講導論-第2講算法分析）

編輯：Python

Python 數據結構

語言基礎：Python
數據結構
- 第一講：DS導論
- - 一、抽象數據類型ADT
  - - 1、通俗比喻：
  - 二、 Python需要注意的問題
- 第二講：算法分析
- - 一、基准技術計算實際執行時間
  - - 1、舉例函數
    - - 1）迭代求和
      - 2）非迭代求和
    - 2、測量技術（時間、內存）
    - - 1）測量執行時間：Time 類
      - 例1：對累加問題sumOfN(r) 計算時間成本
        例2:sumrange(n)平均斜率得出近似擬合曲線(鄰兩點之間的平均斜率)
        例3:polyfit為sum(range(n))數據計算任意次數的最佳擬合多項式函數
      - 2）測量sum(range(n))&sumOfN3(n)執行時間
  - 二、獨立於使用計算機的算法特征
  - - 1、n,T(n),S(n)
    - 2、如何計算S(n)
    - 3、解釋S(n)如何隨著n的大小而變化
    - 4、f(n)=S(n)中起決定性增長的部分
    - - 1）大O的數量級
      - 2）大O的性質
      - 3）[矩陣相乘的時間復雜度分析](https://liwt31.github.io/2018/10/12/mul-complexity/)
    - 3、增長階數描述伸縮性
    - - 1）最好、最壞、普通情況（經典的異序詞檢測問題）
      - 2）比較sumofN(n)&sumofN3(n)算法的優劣
      - 3）各Python數據結構效率（大O性能分析）
      - 創建列表的4種方式：
        列表各種操作的性能分析
        字典與列表性能比較

如果你是大學新生，想學數據結構，最好的語言一定是 Python3

筆記來源 :
Python數據結構與算法第二版(runestone有免費英文版)；
老師上課ppt；

學習步驟：
1、Python
2、Algorithm
3、Basic Data Structure

語言基礎：Python

you can learn it from
by Python 教程

數據結構

第一講：DS導論

一、抽象數據類型ADT

1、通俗比喻：

用戶相當於開車的人；
我們碼農相當於組裝車的人；
（那些零件就是ADT，我們只需要知道怎麼用那些零件就好）
最底層的復雜的基礎工作：怎麼做車零件我們裝的人不用知道；

二、 Python需要注意的問題

第二講：算法分析

Algorithm: ways to solve things.

一個程序的Algorithm好壞決定因素

解決問題時要占用的空間或內存
執行所需的時間進行分析和比較

一、基准技術計算實際執行時間

由於我們不知道使用哪類函數對算法的運行時間表現進行建模，所以這個做法並沒得到有用的度量；所以我們需要找到獨立於所使用的程序或者計算機的算法特征。

1、舉例函數

1）迭代求和

迭代解決函數：

def sumOfN(n):
theSum=0
for i in range(1,n+1):
theSum=theSum+i
return theSum

2）非迭代求和

def sumOfN3(n)利用了一個封閉的方程

#在不迭代的情況下計算n的總和 return (n*(n+1))/2
ns=np.linspace(10,10_000,100,dtype=int)
ts3=[timeit.timrit('sumOfN3(r)',setup=f'r={
n}',number=1000,globals=globals()) for n in ns]
plt.plot(ns,ts3,'ob')

2、測量技術（時間、內存）

1）測量執行時間：Time 類

ps: 測試占用內存：MemoryMonitor類

例1：對累加問題sumOfN 計算時間成本

sum運行時間變化的繪圖函數：

import matplotlib.pyplot as plt
import numpy as np
import timeit
ns=np.linspace(10,10_000,100,dtype=int)#問題規模
ts=[timeit.timeit('sumOfN(r)',setup=f'r={
n}',number=1000,globals=globals())for n in ns]
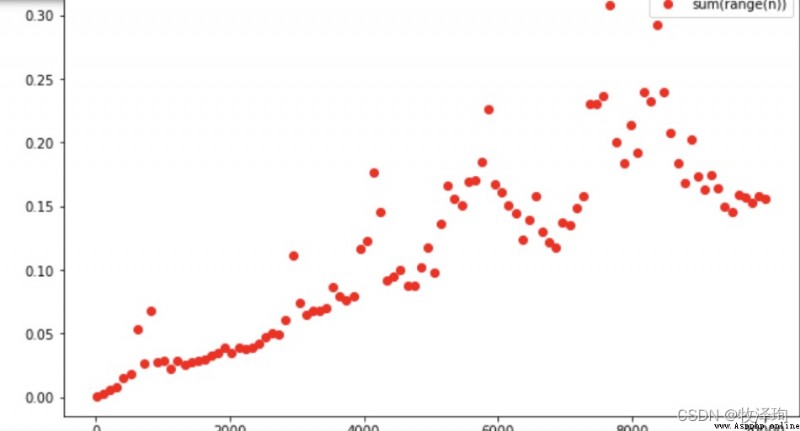
plt.plot(ns,ts,'or')#繪制圖像：問題規模為橫軸，時間成本為縱軸
#ts=[timeit.timeit('sum(r)',setup=f'r=range{n}',number=1000,globals=globals())for n in ns]

例2:sumrange(n)平均斜率得出近似擬合曲線(鄰兩點之間的平均斜率)

total=0
for i in range(len(ns)-1):
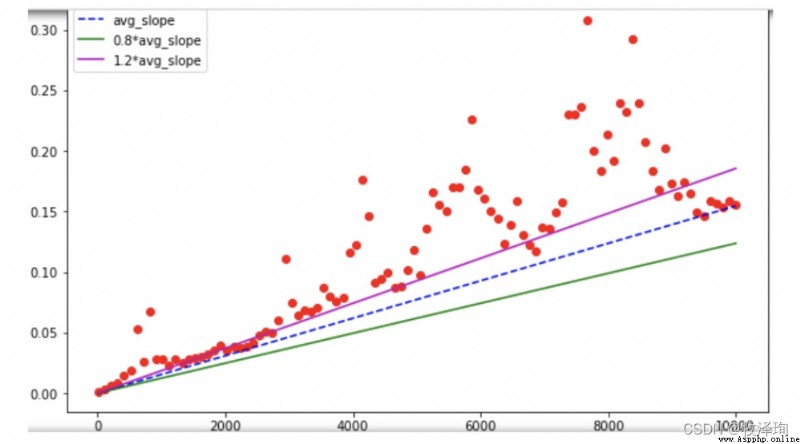
total+=(ts[i+1]-ts[i])/(ns[i+1]-ns[i])# 所有相鄰兩點之間的斜率之和
avg_slope=total/(len(ns)-1)
plt.plot(ns,ts,'or')
plt.plot(ns,[avg_slope*n for n in ns],'--b']
#運行時間估計
for n in np.linspace(1,100_000_000,11,dtype=int)
print(f'Rumtime of sum(range({
n:>11,})~{
avg_slope*n/100:>5.2f}s')
>>>>>Runtime of sum(range( 1)~0.00s
>>>>>Runtime of sum(range(10,000,000)~0.08s

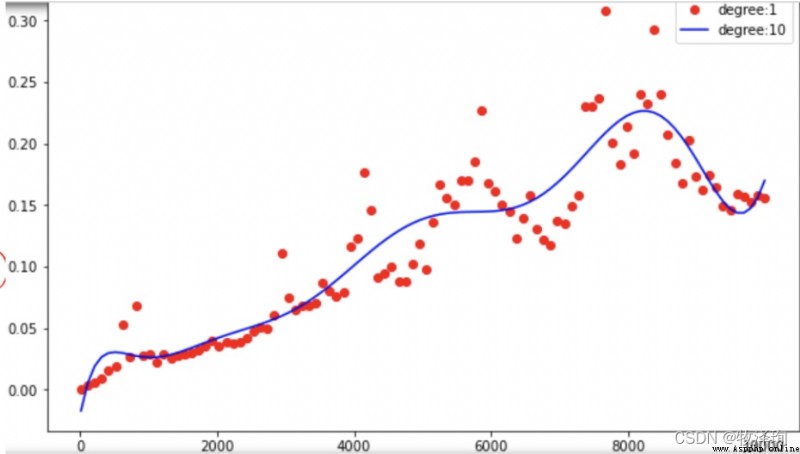
例3:polyfit為sum(range(n))數據計算任意次數的最佳擬合多項式函數

degree=100
coefffs=np.polyfit(ns,ts,degree)
p=np.ploy1d(coeffs)
pt.plot(ns,ts,'or')
plt.plot(ns,[p(n) for n in ns],'-b')
for n in np.linspace(1,100_000_000,11,dtype=int)
print(f'Rumtime of sum(range({
n:>11,})~{
p(n)/100:2f}s')
>>>>>Runtime of sum(range( 1)~0.00s
>>>>>Runtime of sum(range(10,000,000)~929393014.....s

2）測量sum(range(n))&sumOfN3(n)執行時間

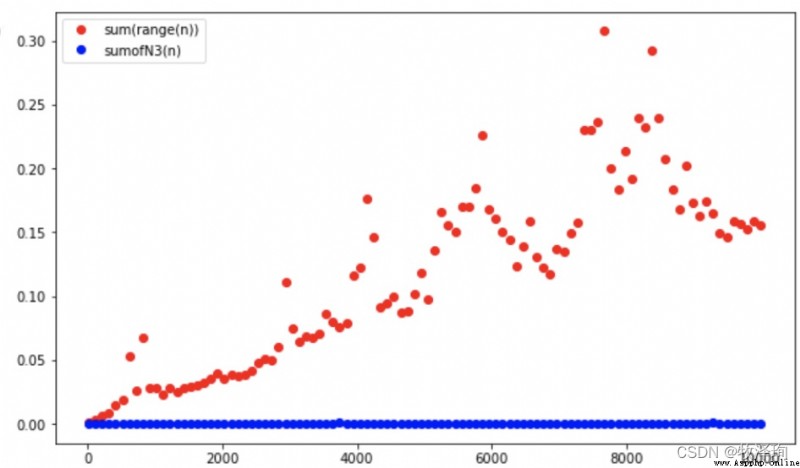
ns=np.linspace(10,10_000,100,dtype=int)
ts=[timeit.timrit('sum(r)',setup=f'r=range({
n})',number=1000,for n in ns]
ts3=[timeit.timeit('sumOfN3(r)',setup=f'r={
n}',number=1000,globals=globals()) for n in ns]
plt.plot(ns,ts,'or')
plt.plot(ns,ts3,'ob')

二、獨立於使用計算機的算法特征

1、n,T(n),S(n)

算法執行時間：可用解決問題所需步驟數進行表示（T（n)=S(n))
問題規模：n
T(n)：解決n的問題所花的時間
S(n）：解決n的問題所需的步驟

2、如何計算S(n)

#程序1 S(n)=5
i=1 #1
j=2 #1
temp=i #1
i=j #1
j=temp #1
#程序2
x=0 #1
n=2 #1
for i in range(1,2*n):#️range(a,b)是從a到b-1
x=x+1#2n-1

3、解釋S(n)如何隨著n的大小而變化

S(n)=O(f(n)) ：算法運行時間增長量級的上界
f(n):S(n)中起決定性增長的部分

4、f(n)=S(n)中起決定性增長的部分

1）大O的數量級

ps:常量階，對數階，線性階，線性對數階，平方階，多項式階，指數階，階乘階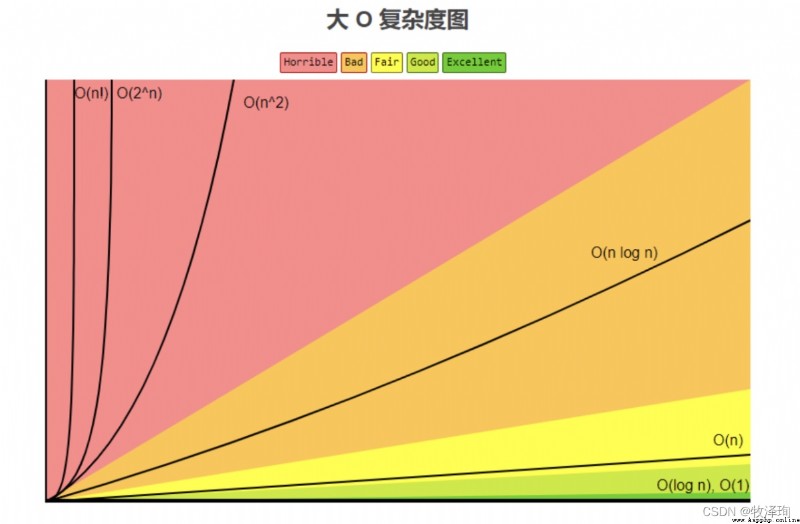

Ps: 指數階與階乘階數量級復雜度為難解問題。

2）大O的性質

取高階：O(n^a + n^b) = O(n^a)
忽略常系數：O(c*f(n))=O(f(n))
O(3n^2) =O(n^2) ； O(5)=O(1)
更復雜的運算原則：
O(f(n))+O(g(n))=O(max{f(n),g(n)})
O(f(n))*O(g(n))=O(f(n)*g(n))

例（函數）：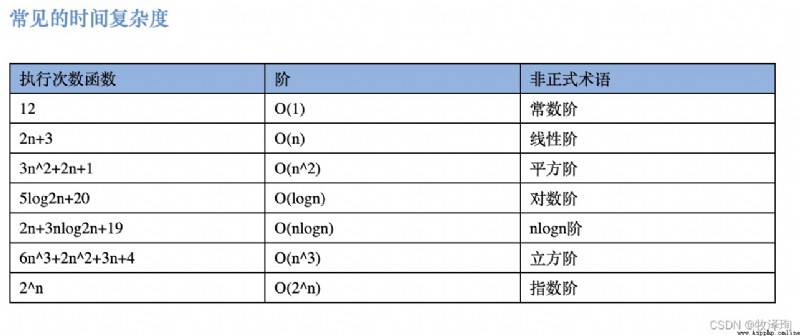

例（程序）：
f(n)：S(n)增長最快的部分
T(n)=O(f(n))=O(n^2)**

#程序1 s(n)=3+(n-1)+(n-1)*(zn+1) f(n)=S(n)增長最快的部分
y=0 #1 T(n)=O(f(n))=O(n^2)
x=0 #1
n=3 #1
for i in range (1,n):
x=y+1#(n-1)
for j in range(2*n+1)
x=x+1#(2n+1)
#程序2 s(n)=n^2 T(n)=O(f(n))=O(n^2)
for i in range(n):#n
for j in range(n):#n
M1[i][j]=M1[i][j]+M2[i][j]

3）矩陣相乘的時間復雜度分析

3、增長階數描述伸縮性

1）最好、最壞、普通情況（經典的異序詞檢測問題）

算法的性能有時不僅依賴於問題規模，
還依賴於數據值。
經典的異序詞檢測問題
1、用None替換相同的元素遍歷
異序詞：一個字符串與另一個字符串所含元素相同，但是排序不同。
S1[0]在S2遍歷，與S2中的元素依次比較直到有相同的出現，將S2中的元素等於None.
每個元素每次情況：

最好：訪問一次就找到了，1
最壞：訪問到最後才找到，n
平均：(1+n)/2
n個元素：n(1+n)/2
時間復雜度：O（n^2)

2、按照字母表順序給字符排序，異序詞得到的結果將是同一個字符串。

Python 中，可以先將字符串轉換為列表，然後使用內建的 sort 方法對列表排序。乍看可能只需要遍歷一次比較基本字符，但是還需要考慮sort()的代價。

3、因為字符可能有26 種，所以使用 26 個計數器，對應每個字符。每遇到一個字符，就將對應的計數器加 1。
ord()函數：
print(ord(‘5’)) # 53
print(ord(‘A’)) # 65
print(ord(’$’)) # 36

def ang(s1,s2):
c1=[0]*26
c2=[0]*26
for i in range(len(s1)):
pos=ord(s1[i])-ord('a')
print(pos)
c1[pos]=c1[pos]+1
print(c1)
for i in range(len(s2)):
pos=ord(s2[i])-ord('a')
c2[pos]=c2[pos]+1
j=0
Stillok=True
while j<26 and Stillok:
if c1[i]==c2[j]:
j=j+1
print(j)
else:
Stillok=False
return Stillok
ang("za","bdca")

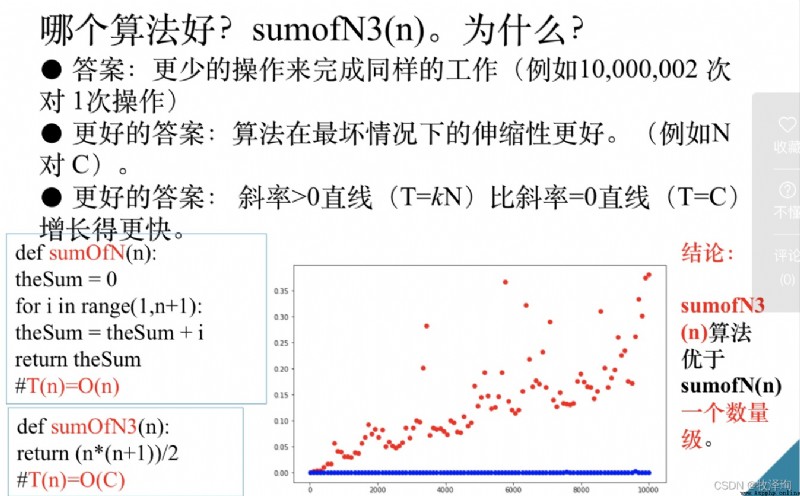
我舉了一個很明顯的例子：
"za"print(pos)print(c1)

觀察結果可以明顯看出pos和c1計數器的用途。

不同數量級的算法
展示不同數量級的算法，

2）比較sumofN(n)&sumofN3(n)算法的優劣

3）各Python數據結構效率（大O性能分析）

創建列表的4種方式：

4種方式

#被測試函數
def test1(n):#連接
l=[]
for i in range(n):
l=l+[i]
def test2(n):#追加
l=[]
for i in range(n):
l.append(i)
def test3(n):#列表解析式
l=[i for i in range(n)]
def test4(n):#range函數+列表構造器
l=list(range(n))

比較四種構造列表方式的效率：繪圖time類函數

#橫軸：問題規模n
ns=np.linspace(10,10_00,100,dtype=int)
#縱軸：解決問題的時間成本
lts1=[timeit.timeit('test1(r)',setup=f'r={
n}',number=100,globals=globals()) for n in ns]
lts2=[timeit.timeit('test2(r)',setup=f'r={
n}',number=100,globals=globals()) for n in ns]
lts3=[timeit.timeit('test3(r)',setup=f'r={
n}',number=100,globals=globals()) for n in ns]
lts4=[timeit.timeit('test4(r)',setup=f'r={
n}',number=100,globals=globals()) for n in ns]
#繪制函數1-4 問題規模n與對應時間成本的函數
plt.plot(ns,lts1,'sb')
plt.plot(ns,lts2,'g')
plt.plot(ns,lts3,'r')
plt.plot(ns,lts4,'K')

列表各種操作的性能分析

POP

#函數
popzero=timeit.Timer("x.pop(0)","from_main_import x")#從列表頭pop出，要遍歷完列表
popend=timeit.Timer("x.pop()","from_main_import x")#從列表尾pop出，與長度無關
#縱軸：時間成本
popendtime=[]
popzerotime=[]
for i in range(10000,1000001,100):
x=list(range(i))
pop_end_t = pop_end.timeit(number=1000)
popendtime.append(pop_end_t)#插入利用timeit函數計算的時間成本數組
x = list(range(i))
pop_zero_t = pop_zero.timeit(number=1000)
popzerotime.append(pop_zero_t)#插入利用timeit函數計算的時間成本數組
#橫軸：
ns=np.linspace(10000,1000001,100,dtype=int)
plt.plot(ns,popendtime,'sb')
plt.plot(ns,popzerotime,'dr')

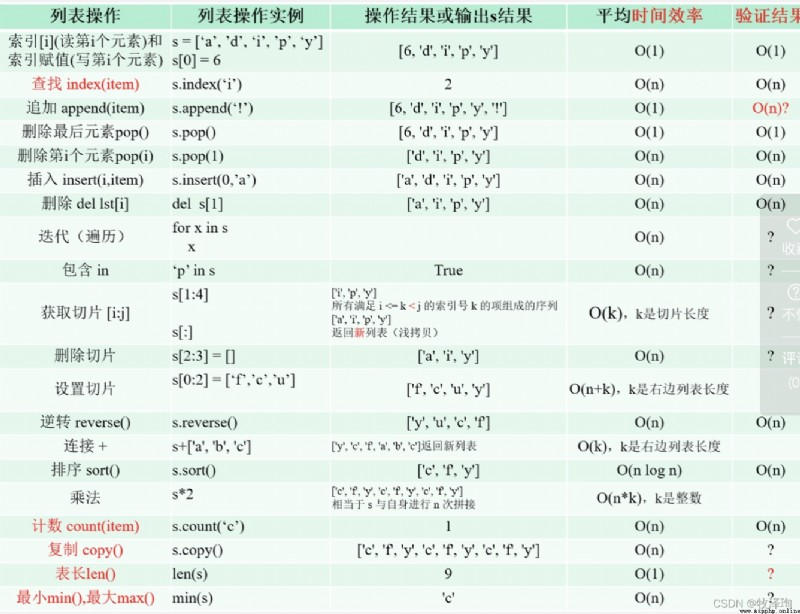
index(x)查找

#函數
index=timeit.Timer("lst.index(x)","from_main_import lst,x")
#縱軸：時間成本
indextime=[]
for n in range(1000,100001,1000):
lst=list(range(n))
x=n//2
index_t=index.timeit(number=1000)
indextime.append(index_t)#插入利用timeit函數計算的時間成本數組
#橫軸：
ns=np.linspace(1000,100000,100,dtype=int)
plt.plot(ns,indextime,'.g',label='index')
plt.lengend()

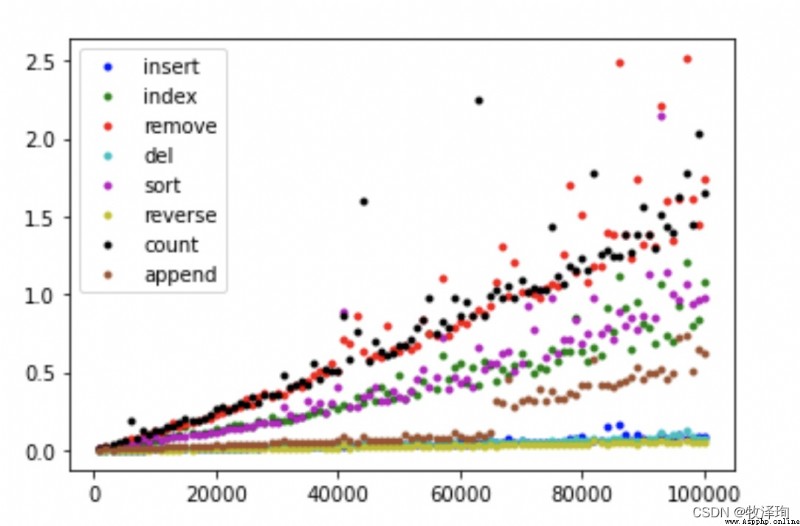
insert(i,x)

#函數
insert=timeit.Timer("lst.index(i,x)","from_main_import lst1,x")
#縱軸：時間成本
inserttime=[]
for n in range(1000,100001,1000):
lst1=list(range(n))
i=0
x=0
insert_t=insert.timeit(number=1000)
inserttime.append(insert_t)#插入利用timeit函數計算的時間成本數組
#橫軸：
ns=np.linspace(1000,100000,100,dtype=int)
plt.plot(ns,insertime,'.b',label='insert')
plt.lengend()

remove(x)

remove=timeit.Timer("lst2.remove(x)","from_main_import lst2,x")

del lst[i]

delete=timeit.Timer("del lst3a[i][0];i=i+1","from_main_import lst3a,i")

sort()

sort=timeit.Timer("lst4.reverse()","from_main_import lst4")

reverse()

reverse=timeit.Timer("lst5.reverse()","from_main_import lst5")

count(x)

count=timeit.Timer("lst6.count(x)","from_main_import lst6,x")

append(x)

append=timeit.Timer("lst7a[i].append(0);i+=","from_main_import lst7a,i")

列表索引賦值操作[ ]

#函數
idexassign=timeit.Timer("lst8[i]=0)","from_main_import lst8,i")
#縱軸：時間成本
idxassigntime=[]
for n in range(10000,1000001,10000):
lst1=list(range(n))
i=n//2
idxa_t=idxassign.timeit(number=1000)
inserttime.append(idxa_t)#插入利用timeit函數計算的時間成本數組
#橫軸：
ns=np.linspace(10000,1000001,100,dtype=int)
plt.plot(ns,idxassigntime,'.','color='darkorange',![請添加圖片描述](https://img-blog.csdnimg.cn/5e66689e05664f189d11b8b87301facb.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA54mn5rO954-j,size_20,color_FFFFFF,t_70,g_se,x_16)
label='insert')
plt.lengend()

字典與列表性能比較

判斷隨機數在列表和字典是否存在的時間對比

import timeit
import random
#定義 存儲時間的數組
lst_timelst=[]
d_timelst=[]
for i in range((10000, 1000001, 20000):
t=timeit.Timer("random.randrange(%d)in x"%i,"from_main_import random,x")
x=list(range(i))#列表構造器
list_time=t.timeit(number=1000)
#列表數組存入所得對應時間成本
lst_timelst.append(list_time)
x={
j:None for j in range(i))
d_time=t.timeit(number=1000)#字典構造
#字典數組存入所得對應時間成本
d_timelst.append(d_time)
#drawing the curve
plt.plot(ns,lst_timelst,'.b',label='list')#列表
plt.plot(ns,d_timelst,'.r',label='dict')#字典
#我沒有寫輸出操作