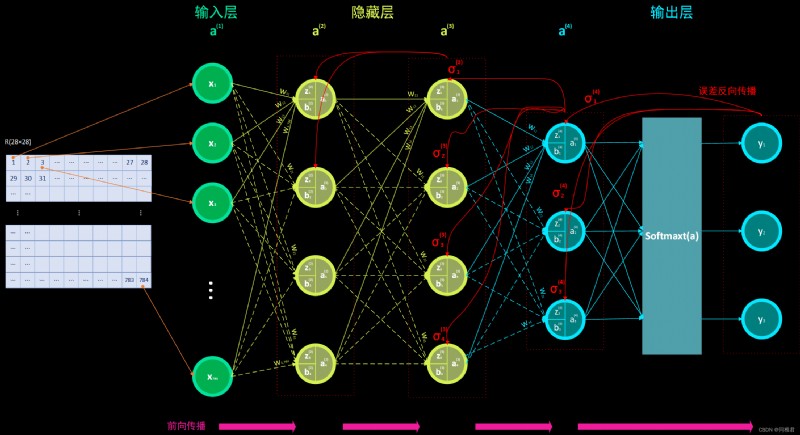
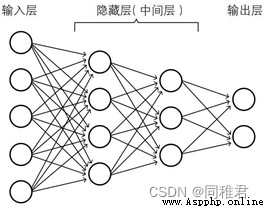
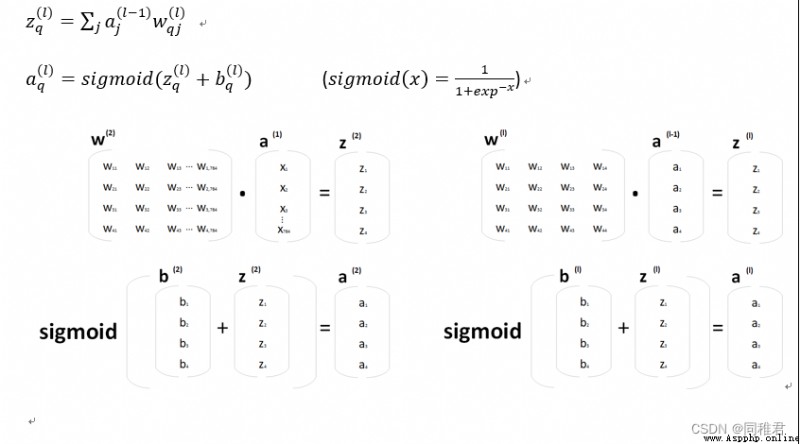
本文構建的全連接神經網絡模型結構圖如上。其中中間隱藏層的數量以及各層（輸入層、隱藏層、輸出層）的神經單元數量均可 自由設置，本文構造的神經網絡並不是專門為識別手寫數字而寫死的，而是可以根據 任務的需要，自由改變神經網絡的參數（如層數、神經單元數、學習率、學習率衰減值 等）。在本文裡以識別手寫數字為例，輸出層的神經單元數為 9，結構圖為了能夠表示得更清晰（使其看 起來不混亂），遂只繪制了 3 個神經單元。
本文已將神經網絡模型程序封裝成類，神經網絡的各參數為類中屬性，神經網絡的生成、訓練、預測、保存、評估等為類中方法，以便可以更加快捷地調用，同時降低代碼冗余、提高代碼可讀性。
本文作者：A WHU SIM Student
目錄
1.引言
2.涉及的神經網絡知識原理
2.1神經網絡思想
2.2激活函數
2.2.1sigmoid激活函數
2.2.2softmax激活函數
2.3交叉熵損失
2.4小批量梯度下降法
2.5誤差反向傳播法
2.6手寫數字數據集
2.7Python面向對象編程
3.詳細計算推導
3.1各符號解釋
3.2前向傳播部分
3.3小批量梯度下降部分
3.4誤差反向傳播部分
4.代碼實現
4.1本文神經網絡UML類圖如下：
4.2用到的第三方庫有：
4.3模型包含的屬性與方法部分代碼如下：
4.4模型功能：
4.5模型訓練與預測中的部分截圖：
4.6包含6萬條手寫數據的數據集+本文章構建的全連接神經網絡模型+訓練好的准確率為93.21%的全連接神經網絡模型:全連接神經網絡
人工神經網絡（artificial neural network，ANN）是一種模仿生物神經網絡的結構和功能的數學模型或計算模型。神經網絡由大量的人工神經元聯結進行計算。大多數情況下人工神經網絡能在外界信息的基礎上改變內部結構，是一種自適應系統。現代神經網絡是一種非線性統計性數據建模工具，常用來對輸入和輸出間復雜的關系進行建模，或用來探索數據的模式。
生物神經網絡的主要工作原理如下：
①神經元形成網絡。
②對於從其他多個神經元傳遞過來的信號，如果它們的和不超過某個固定大小的值（阈值)，則神經元不做出任何反應。
③對於從其他多個神經元傳遞過來的信號，如果它們的和超過某個固定大小的值（阈值)，則神經元做出反應（稱為點火)，向另外的神經元傳遞固定強度的信號。
④在②和③中，從多個神經元傳遞過來的信號之和中，每個信號對應的權重不一樣。
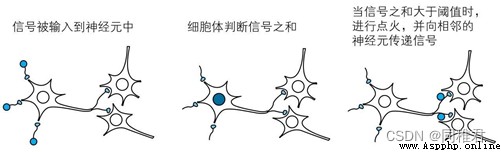
將神經元的工作在數學上抽象化，並以其為單位人工地形成網絡，這樣的人工網絡就是神經網絡。將構成大腦的神經元的集合體抽象為數學模型，這就是神經網絡的出發點。
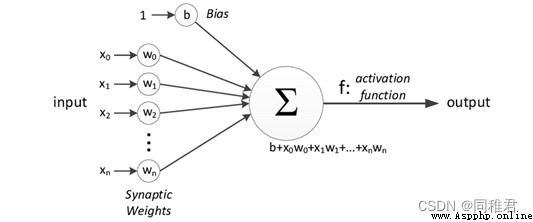
單個人工神經單元結構如下圖：
多個神經單元組成的神經網絡如下圖：
激活函數對於ANN學習和理解真正復雜的東西很重要。它們的主要目的是將ANN中節點的輸入信號轉換為輸出信號，此輸出信號將作為下一層的輸入。常用激活函數有：單位階躍激活函數、Sigmoid激活函數、tanh雙曲正切激活函數、ReLU整流線性單元激活函數、softmax激活函數。本文使用的是sigmoid（中間層使用）和softmax激活函數（輸出層使用）。
Sigmoid函數是一個有著優美S形曲線的數學函數，在邏輯回歸、人工神經網絡中有著廣泛的應用。
公式：
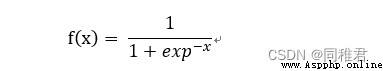
導數：
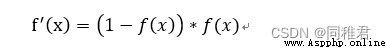
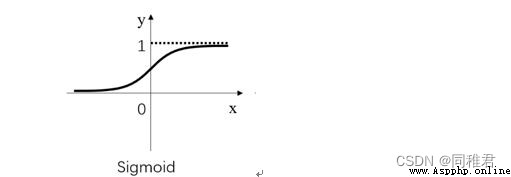
圖像：
優點：平滑、易於求導。
缺點：激活函數計算量大（在正向傳播和反向傳播中都包含冪運算和除法）；Sigmoid導數取值范圍是[0, 0.25]，由於神經網絡反向傳播時的“鏈式反應”，很容易就會出現梯度消失的情況。例如對於一個10層的網絡， 根據 0.25^10 ≈ 0.000000954，第10層的誤差相對第一層卷積的參數 W1 的梯度將是一個非常小的值，這就是所謂的“梯度消失”；Sigmoid的輸出不是0均值（即zero-centered）；這會導致後一層的神經元將得到上一層輸出的非0均值的信號作為輸入，隨著網絡的加深，會改變數據的原始分布。
softmax用於多分類過程中，它將多個神經元的輸出，映射到（0,1）區間內，可以看成概率來理解，從而來進行多分類，其多用於神經網絡的最後一次層。
公式：
導數：
對 softmax 導數，就是求第 i 項的輸出對第 j 項輸入的偏導：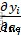
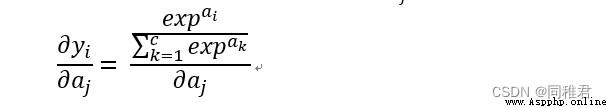
當i=j時：
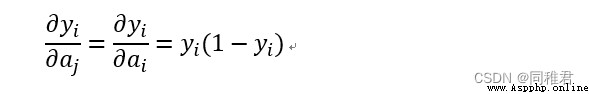
當i != j時：
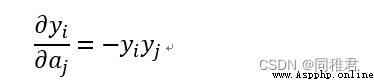
優點：softmax 是用於多類分類問題的激活函數，在多類分類問題中，超過兩個類標簽則需要類成員關系。對於長度為 K 的任意實向量，softmax 可以將其壓縮為長度為 K，值在（0，1）范圍內，並且向量中元素的總和為 1 的實向量。
缺點：在零點不可微，負輸入的梯度為零，這意味著對於該區域的激活，權重不會在反向傳播期間更新，因此會產生永不激活的死亡神經元。
交叉熵是信息論中的概念，最初用於估算平均編碼長度。給定兩個概率分布p和q，通過q來表示p的交叉熵為：
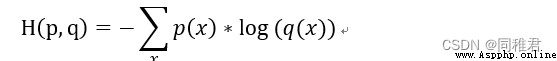
交叉熵損失（Cross-entropy cost）是用來衡量深度神經網絡（DNN）預測的概率分布與實際概率分布的差異的一種方式。它刻畫的是實際輸出（概率）與期望輸出（概率）的距離，即交叉熵損失的值越小，兩個概率分布就越接近。與平方損失相比，它能更有效地促進訓練全連接神經網絡。若𝒚𝒊為標簽值， 𝑦𝑖′為預值測，則交叉熵損失為：
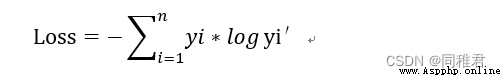
梯度下降法基於的思想是：要找到某函數的最小值，最好的方法是沿著該函數的梯度方向的反方向探尋。如果梯度記為 ∇，則函數 f(x,y)的梯度由下式表示：
這個梯度意味著要沿 x 的方向移動 -∂ f ( x，y ) /∂ x，沿 y 的方向移動- ∂ f ( x ，y )/ ∂ y。其中，函數 f(x,y)必須要在待計算的點上有定義並且可微。梯度下降算法到達每個點後都會重新估計移動的方向。從 P0 開始，計算完該點的梯度，函數就根據梯度移動到下一點 P1。在 P1 點，梯度再次被重新計算，並沿新的梯度方向移動到 P2。如此循環迭代，直到滿足條件。迭代的過程中，梯度算子總是保證我們能選取到最佳的移動方向。偏導數確定了移動的方向，再由學習率α確定移動步長，用向量來表示的話，梯度下降算法的迭代公式如下：
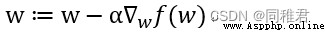
小批量梯度下降（Mini-Batch Gradient Descent），是對全批量梯度下降以及隨機梯度下降的一個折中辦法。其思想是：每次迭代使用多個小批量的樣本來對參數進行更新，每個小批量中含有“batchSize”個樣本。其優點是每次使用一個小批量樣本可以大大減小參數收斂所需要的迭代次數，同時可以使收斂到的結果更加接近梯度下降的效果。在一定范圍內，一般來說“batchSize”越大，其確定的下降方向越准，引起訓練震蕩越小。
誤差反向傳播算法（back propagation，簡稱BP模型）是1986年由Rumelhart和McClelland為首的科學家提出的概念，是一種按照誤差逆向傳播來訓練多層前饋神經網絡的算法。其系統的解決了多層神經網絡隱含層連接權學習問題，人們把采用這種算法進行誤差校正的多層前饋網絡稱為BP網。在實驗過程中將會給出反向傳播計算的詳細過程。
手寫數字數據格式有兩種形式：
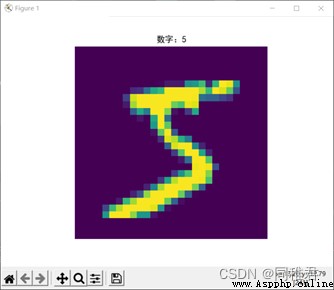
①MNIST數據集，是由0到9的數字圖像構成。其中訓練圖像有6萬張，測試圖像有1萬張，手寫數字由250個不同的人手寫而成。每一張圖片都有對應的標簽數字，圖像像素均為28*28。圖像並不以圖像文件形式存儲，而是由28*28的數組表示，數組中的每個元素與每個像素相對應，通過matplotlib可以將數組表示的圖像顯示出來。用於訓練與分類時，需要將28*28的數組轉換成1*784的向量。
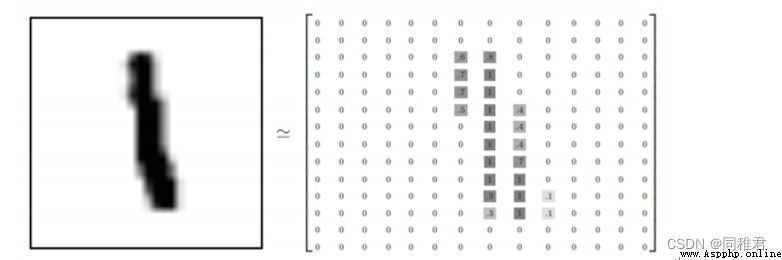
②另一個數字數據集是以文本形式保存的，每一個數字保存在一個txt文本中，數字通過只包含0與1的32*32的數組表示，如數字“4”的表示如下圖：
本文使用的數據集為①中數據集。
面向對象（英文是Object Oriented，縮寫為OO）面向對象是一種軟件開發方法，一種編程方式。通常情況下，我們把對象分為兩個部分：靜態部分和動態部分。其中靜態部分我們稱為“屬性”，任何的對象都有自己的屬性，是客觀存在的，如人的性別高矮胖瘦等屬性；動態部分是指對象的行為，如人的走路，吃飯，睡覺等可以執行的動作行為。在Python中，類是封裝對象的屬性和行為的載體。封裝是面向對象編程的核心思想，將對象的屬性和行為封裝起來，而講對象的屬性和行為封裝起來的載體就是類。封裝就是隱藏對象的屬性和實現細節，僅對外公開接口，控制在程序中屬性的讀和修改的訪問級別，將抽象得到的數據和行為(或功能)相結合，形成一個有機的整體，也就是將數據與操作數據的源代碼進行有機的結合，形成“類”，其中數據和函數都是類的成員。
本文將神經網絡封裝成類，神經網絡的各參數為類中屬性，神經網絡的生成、訓練、預測、保存、評估等為類中方法，以便可以更加快捷地調用，同時降低代碼冗余、提高代碼可讀性。
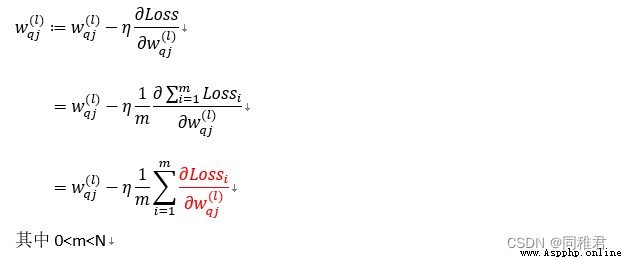
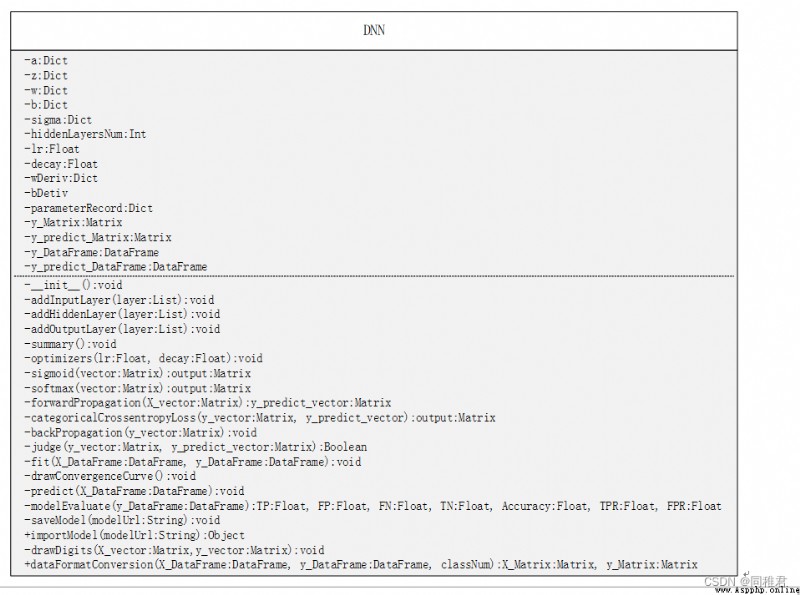
class DNN:
def __init__(self): #初始化模型
self.a = {} # 用於存放各層各神經單元輸出的字典
self.z = {} # 用於存放各層各神經單元輸入的字典
self.w = {} # 用於存放各層之間w參數的字典
self.b = {} # 用於存放各層各神經單元偏置的字典
self.sigma = {} # 用於存放反向傳播時各層各神經單元sigma值的字典
self.hiddenLayersNum = None # 用於記錄隱藏層層數，便於計算出輸出層的索引
# self.y = None # 用於保存經過softmax函數激活後的輸出的numpy列向量
self.lr = 0.01 # 設置初始學習率，默認值為0.01
self.decay = 0 # 設置每輪迭代學習率衰減值，默認為0
self.wDeriv = {} # 記錄 Li 對 w 的偏導的累加和
self.bDeriv = {} # 記錄 Li 對 b 的偏導的累加和
self.parameterRecord = {} # 用於記錄某些指定參數在每輪迭代後的值，便於繪制參數收斂曲線
self.y_Matrix = None # 待預測的樣本的類別矩陣
self.y_predict_Matrix = [] # 用於保存模型預測結果的矩陣
self.y_DataFrame = None
self.y_predict_DataFrame = None
# 添加輸入層的方法，參數layer為列表，其列表元素只有一個，用於指定輸入層的神經單元個數
def addInputLayer(self, layer):
# 添加隱藏層的方法，參數layer為列表，其列表元素個數代表添加的隱藏層層數，每一個元素指定其對應的隱藏層所含的神經單元個數
def addHiddenLayer(self, layer):
# 添加輸出層，參數layer為列表，其元素只有一個，代表輸出層神經單元個數（即分類類別個數）
def addOutputLayer(self, layer):
# 用於查看各層詳情
def summary(self):
# sigmoid函數，輸入列向量，返回計算後的列向量
def sigmoid(self, vector):
# softmax激活函數，輸入列向量，返回計算後的列向量
def softmax(self, vector):
# 前向傳播，參數 X_vector 為某樣本特征向量，返回 y_predict_vector 該樣本預測類別向量
def forwardPropagation(self, X_vector):
# 計算多分類交叉熵損失
def categoricalCrossentropyLoss(self, y_vector,y_predict_vector):
# 反向傳播, 參數為該樣本真實類別標簽 y_vector.shape = (1, 10) ，用於計算輸出層的sigma值
def backPropagation(self, y_vector):
def judge(self, y_vector, y_predict_vector):
# 模型訓練
'''
參數 X_Matrix 為訓練樣本特征值矩陣（每一行為一個樣本）
y_Matrix為訓練樣本類別標簽矩陣（每一行為一個樣本）
epochs為迭代輪數（默認為20輪）
batchSize為使用小批量梯度下降算法時每個小批量的樣本數目
parameterList 描述需要記錄的參數，如[("w",2,4,3), ("b", 2, 1)] 表示需要記錄 第1層第3個神經元到第2層第4個神經元的權重w 和 第2層第1個神經元的偏置b
'''
# ，，epochs為迭代輪數（默認為20輪），
def fit(self, X_Matrix, y_Matrix, epochs=20, batchSize=30, parameterList = None):
# 根據self.parameterRecord繪制參數收斂曲線的函數
def drawConvergenceCurve(self):
# 模型預測
def predict(self, X_Matrix):
# 模型評估
def modelEvaluate(self, y_Matrix):
# 初始化交叉熵損失
L = 0.0
# 初始化准確率
accuracy = 0
# 保存模型 實例方法
def saveModel(self, modelFileUrl):
f = open(modelFileUrl, 'wb')
@classmethod # 類方法，用於調用模型
def importModel(cls, modelFileUrl):
f = open(modelFileUrl, 'rb')
# 繪制手寫數字
def drawDigits(self, X_vector, y_vector):
plt.imshow(X_vector.reshape(28, 28)) # cmap="gray"
@classmethod # 類方法，用於轉換數據格式，輸入的是pandas數組，返回numpy矩陣，以便於神經網絡的計算
def dataFormatConversion(cls, X_DataFrame,y_DataFrame, classNum):
# 將y_DataFrame由列向量轉為行向量，
1.任意設置輸入層、隱藏層、輸出層中各層的神經單元個數；
2.任意設置隱藏層層數；任意設置學習率、學習率衰減值，從而滿足不同的學習率衰減策略；
3.任意設置迭代輪數；
4.任意設置小批量中的樣本數；
5.能夠根據給定的數組還原手寫數字圖像；
6.能夠繪制指定參數的迭代收斂曲線。
7.能夠保存訓練好的模型（保存在txt文件中），這樣就可以只訓練一次，下次要用時直接調用訓練好的模型，而不需要再次訓練。
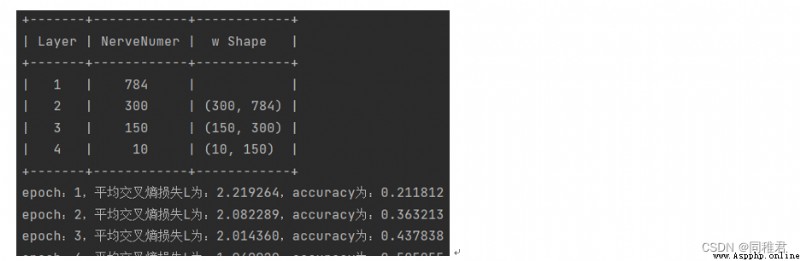
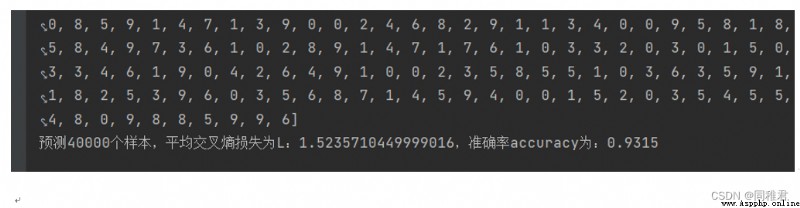
經過一天的等待，最終模型對2萬個訓練數據的預測准確率為0.9321，交叉熵損失為1.5233。
繪制參數收斂曲線，其中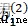
的500輪迭代的收斂曲線如下圖:
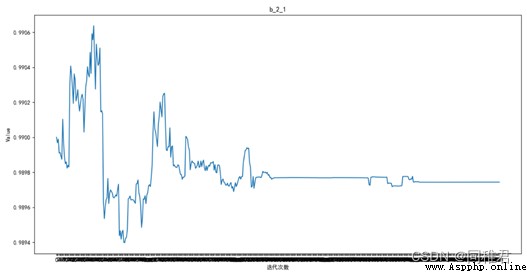
模型繪制的數據集中的第一個數字“5”：
