股票市場易受到諸多不確定性因素的影響,因此股價預測問題挑戰巨大,自提出以來就是數字金融中的熱門研究領域。傳統簡單的K線、十字線法操作簡單,但預測准確率難以令人滿意。隨著該研究領域的不斷深入,各種模型方法層出不窮。為比較各類模型的性能,本文選取了四種代表模型,線性模型中的移動平均、線性回歸,傳統機器學習模型KNN,深度學習模型LSTM,分別使用四種模型對深股平安銀行的股價進行擬合預測。綜合對比發現,深度網絡以其獨有的優勢在高噪聲、波動大、非線性的金融時序數據上表現出色,深度學習為股價的預測提供了新的思路。最後本文使用LSTM模型對平安銀行未來30個工作日的股價走勢進行預測並對投資者提出相關建議。
本文使用的數據集為2012年12月31日至2022年6月10日的深交個股平安銀行的日線歷史行情數據,共2290條。通過調用數據接口從tushare pro平台上獲取,tushare是一個python的金融數據接口包,當前開源免費,幫助數據分析師在數據獲取上減輕了很多壓力。主要由上交所、深交所、騰訊財經、新浪、鳳凰財經等向tushare提供的一些股票證券方面的數據,其中包括歷史數據、實時數據、分類數據、基本面數據、宏觀經濟數據、網絡輿情、新聞事件數據等等,為金融市場的數據分析和金融產品的開發提供了很好的工具。本文的數據就是由深圳交易所提供,真實可靠。數據集中共有股票代碼(ts_code)、交易日期(trade_date)、開盤價(open)、最高價(high)、最低價(low)、收盤價(close)、昨收價(pre_close)、漲跌額(change)等11種變量。如圖一所示:

本文中數據預處理的工作主要包括檢查數據中是否存在缺失值,將字符型的日期轉換成Datatime日期型。因數據集較為干淨整潔,減少了大量預處理工作。
import tushare as ts
token='******' #此處寫自己的api接口token
pro = ts.pro_api(token)
#平安銀行股票數據下載
df = pro.daily(ts_code='000001.SZ', start_date='20121231', end_date='20220612')
df.to_csv('平安銀行歷史行情1.csv')#import packages
import pandas as pd
import numpy as np
#to plot within notebook
import matplotlib.pyplot as plt
%matplotlib inline
#setting figure size
from matplotlib.pylab import rcParams
rcParams['figure.figsize'] = 20,10
#for normalizing data
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler(feature_range=(0, 1))
#read the file
df = pd.read_csv('平安銀行歷史行情1.csv',index_col=0)
#print the head
df.head()otput:
#定義將int類型日期轉換成dataframe類型
def string_to_date(string: str) -> str:
"""字符串轉日期格式"""
from datetime import datetime
shift_datetime = datetime.strptime(string, '%Y%m%d') # 字符串 -> 時間
shift_date = shift_datetime.strftime("%Y-%m-%d") # 時間 -> 任意時間格式
return shift_date
def convert_date_from_int(time_series: pd.Series):
"""整形的series -> pandas時間格式"""
time_series = time_series.astype('str').apply(string_to_date)
return pd.to_datetime(time_series)output:
簡單分析各變量代表意義,股票的開票價和收盤價代表某一天該股的起始價和最終價;最高價、最低價表示某一天股票成交最高價和最低價;漲跌額和漲跌幅是相對於前一天相比該股收盤價的變動額和變動幅度;成交量代表該天交易的股票總數;成交額代表某公司該天的營業額。數據中記錄的是工作日股票交易數據,因此會存在一些日期的缺失,不需要額外進行填充處理,處理後反而會影響預測結果。一般來說,股票的漲跌損益是由收盤價來決定的,因此股票預測的目標變量是收盤價。我們分析的是金融時序數據,因此自變量是時間。
首先觀察收盤價的趨勢圖:
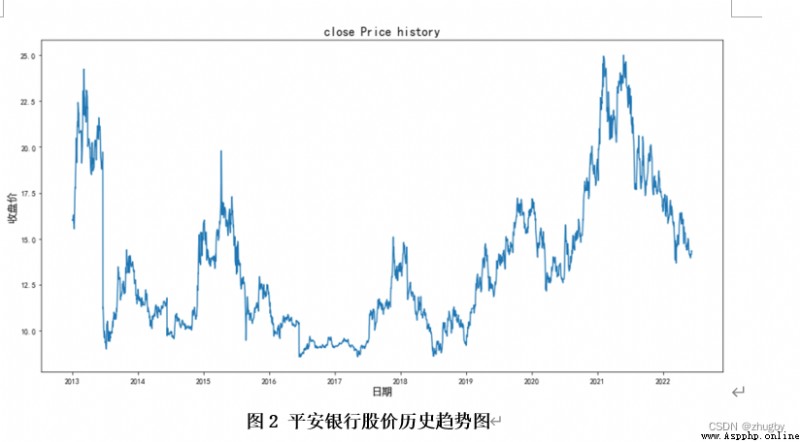
df['trade_date']= convert_date_from_int(df['trade_date'])
df.index = df['trade_date']
#setting index as date
#plot
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(16,8))
plt.plot(df['close'], label='close price history')
plt.title('close Price history',fontsize=16)
plt.xlabel('日期',fontsize=14)
plt.ylabel('收盤價',fontsize=14)時間序列數據的預測需要劃分訓練測試集,本文中將2012-12-31至2021-12-31日十年的數據作為訓練集,將2022-01-04至2022-06-10的數據作為測試集。如下圖所示:
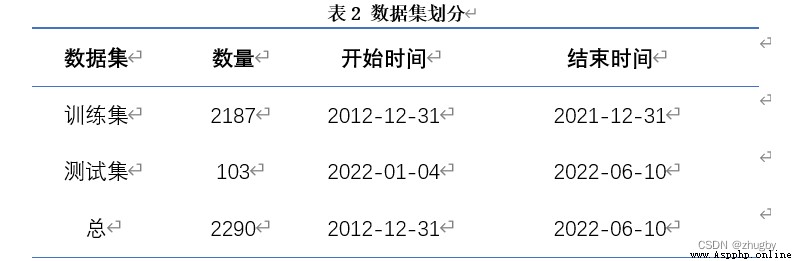
#creating dataframe with date and the target variable
data = df.sort_index(ascending=True, axis=0)
new_data = df[['trade_date', 'close']].sort_index(ascending=True, axis=0)
new_data.head()
#splitting into train and validation
valid = new_data[2187:]
train = new_data[:2187]
觀察測試訓練集大小和起始時間:
new_data.shape, train.shape, valid.shapeoutput:
train['trade_date'].min(), train['trade_date'].max(), valid['trade_date'].min(), valid['trade_date'].max()output:
LSTM模型於1997年由Hochreiter & Schmidhuber [1]提出,是RNN的一種變體,全稱Long short-Term Memory,即長短時記憶人工神經網絡模型[2]。顧名思義,它是一個具有長短期信息存儲能力的神經網絡。經過多年的發展,加上深度學習熱潮掀起之後學者們的不斷改善,當前LSTM網絡已經形成了較為系統完善的架構,並且廣泛應用於多個領域。
循環神經網絡(RNN)、BP神經網絡都會面臨當網絡層加深之後反向傳播產生梯度消失或梯度爆炸的問題,難以表示長期依賴關系。為了解決這種長期依賴問題,LSTM在傳統RNN的基礎上引入了門控單元(gate)來控制信息的傳遞,包含三個門:遺忘門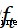 ,輸入門
,輸入門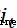 ,輸出門
,輸出門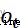 。遺忘門決定了上一個細胞狀態
。遺忘門決定了上一個細胞狀態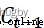 的信息多少需要丟棄,輸入門決定保存細胞狀態
的信息多少需要丟棄,輸入門決定保存細胞狀態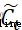 的哪些新生信息,輸出門決定在該時刻
的哪些新生信息,輸出門決定在該時刻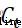 需要輸出到外部的信息[3]。
需要輸出到外部的信息[3]。
LSTM通過三個門來處理時序數據,首先通過遺忘門,遺忘門數學表達式如下:
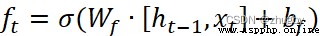
(1)
其中,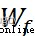 和
和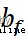 分別表示遺忘門的權重和偏置參數。
分別表示遺忘門的權重和偏置參數。
通過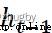 和
和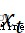 輸出一個0到1之間的向量,決定上一個細胞狀態多少信息需要遺忘,0表示全部丟棄,1表示全部接受。
輸出一個0到1之間的向量,決定上一個細胞狀態多少信息需要遺忘,0表示全部丟棄,1表示全部接受。
然後信息被傳遞到輸入門,輸入門包括兩部分,1)sigmoid激活得到更新狀態it 2)tanh激活得到候選狀態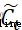 ,公式如下:
,公式如下:
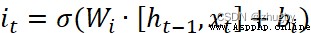
(2)
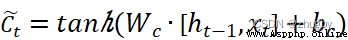
(3)
其中, 、
、 表示權重參數,
表示權重參數,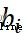 、
、 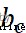 表示偏置參數
表示偏置參數
經輸入門後,上一個細胞信息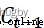 更新為
更新為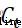 ,最後通過輸出門決定要輸出哪些信息。輸出門同樣包含兩個部分,1)sigmoid 層2)tanh層,與輸出門不同的是,sigmoid 層決定要輸出細胞狀態中的哪些部分,tanh層變換調整細胞狀態值得到0-1之間的向量再乘以細胞狀態Ct
,最後通過輸出門決定要輸出哪些信息。輸出門同樣包含兩個部分,1)sigmoid 層2)tanh層,與輸出門不同的是,sigmoid 層決定要輸出細胞狀態中的哪些部分,tanh層變換調整細胞狀態值得到0-1之間的向量再乘以細胞狀態Ct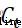 得到最終的輸出。具體數學表達式如下:
得到最終的輸出。具體數學表達式如下:
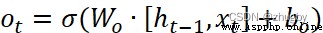
(4)
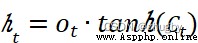
(5)
其中,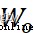 代表sigmoid激活函數層的權重參數,
代表sigmoid激活函數層的權重參數,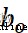 代表sigmoid激活函數層的偏置參數。
代表sigmoid激活函數層的偏置參數。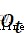 代表sigmoid激活函數層的輸出,
代表sigmoid激活函數層的輸出,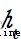 代表該時刻記憶單元的輸出,即隱含狀態。
代表該時刻記憶單元的輸出,即隱含狀態。
門控單元原理圖如下所示:
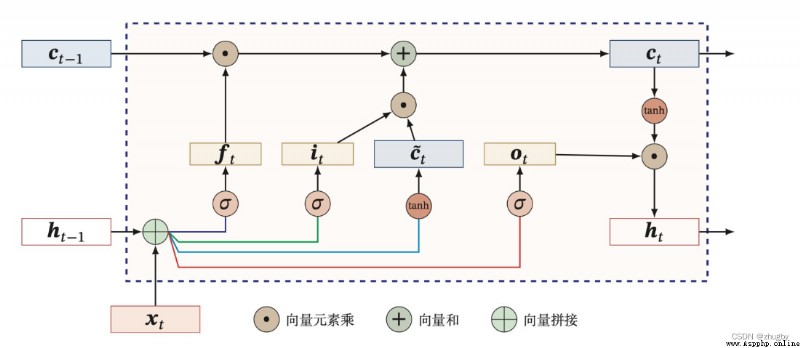
圖3 LSTM門控單元原理圖
將各個細胞/門控單元連接起來就變成了LSTM的整體架構,如下圖所示:
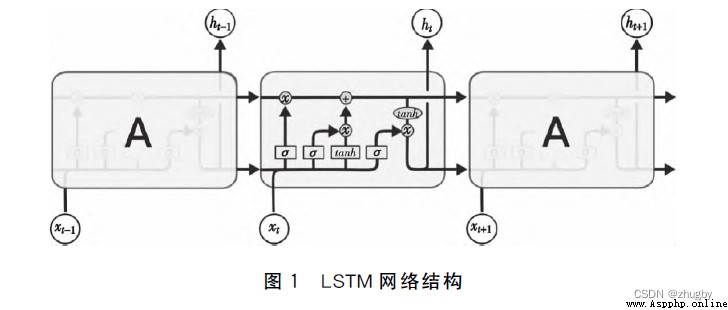
圖4 LSTM網絡結構
本文中使用均方誤差RMSE作為模型評價的指標,均方誤差RMSE衡量的是模型的預測值和真實值的差異,經常用做機器學習預測結果衡量的標准。如公式(1)所示:
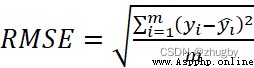
(6)
計算均方誤差,得RMSE=0.5793,用可視化圖形展示預測結果。
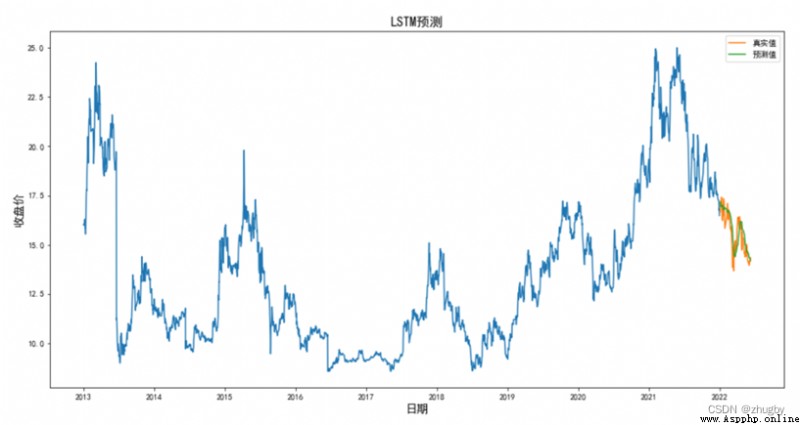
結合RMSE值和圖形,LSTM算法擬合程度高,在預測准確率上表現出色。
#importing required libraries
from sklearn.preprocessing import MinMaxScaler
from keras.models import Sequential
from keras.layers import Dense, Dropout, LSTM
#setting index
data = df.sort_index(ascending=True, axis=0)
new_data = data[['trade_date', 'close']]
new_data.index = new_data['trade_date']
new_data.drop('trade_date', axis=1, inplace=True)
new_data.head()
#creating train and test sets
dataset = new_data.values
train= dataset[0:2187,:]
valid = dataset[2187:,:]
#converting dataset into x_train and y_train
scaler = MinMaxScaler(feature_range=(0, 1))
scaled_data = scaler.fit_transform(dataset)
x_train, y_train = [], []
for i in range(60,len(train)):
x_train.append(scaled_data[i-60:i,0])
y_train.append(scaled_data[i,0])
x_train, y_train = np.array(x_train), np.array(y_train)
x_train = np.reshape(x_train, (x_train.shape[0],x_train.shape[1],1))
# create and fit the LSTM network
model = Sequential()
model.add(LSTM(units=50, return_sequences=True, input_shape=(x_train.shape[1],1)))
model.add(LSTM(units=50))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
model.fit(x_train, y_train, epochs=1, batch_size=1, verbose=1)
#predicting 246 values, using past 60 from the train data
inputs = new_data[len(new_data) - len(valid) - 60:].values
inputs = inputs.reshape(-1,1)
inputs = scaler.transform(inputs)
X_test = []
for i in range(60,inputs.shape[0]):
X_test.append(inputs[i-60:i,0])
X_test = np.array(X_test)
X_test = np.reshape(X_test, (X_test.shape[0],X_test.shape[1],1))
closing_price = model.predict(X_test)
closing_price1 = scaler.inverse_transform(closing_price)
rms=np.sqrt(np.mean(np.power((valid-closing_price1),2)))
rms
#v=new_data[2187:]
valid1['Pre_Lstm'] = closing_price1
train=new_data[:2187]
plt.figure(figsize=(16,8))
plt.plot(train['close'])
plt.plot(valid1['close'],label='真實值')
plt.plot(valid1['Pre_Lstm'],label='預測值')
plt.title('LSTM預測',fontsize=16)
plt.xlabel('日期',fontsize=14)
plt.ylabel('收盤價',fontsize=14)
plt.legend(loc=0)
為了更加清晰的展現lstm模型性能,本文選取了四種代表模型,線性模型中的移動平均、線性回歸,傳統機器學習模型KNN,深度學習模型LSTM,分別使用四種模型對深股平安銀行的股價進行擬合預測。表4展示了四個模型的部分預測數值,圖12對比展示了四個模型的股價預測趨勢,表5展示了四個模型的RSME值。
表4 部分測試集模型預測數值
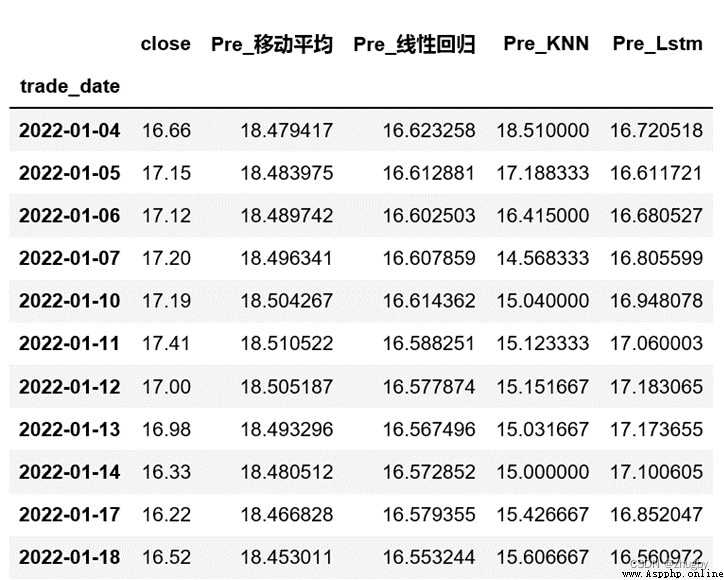
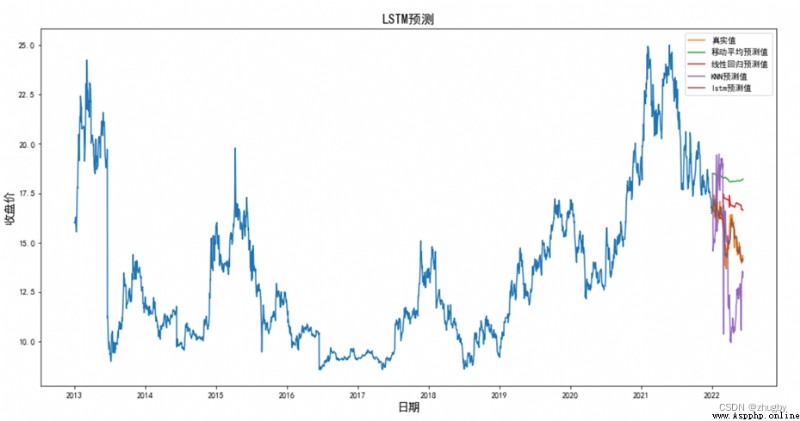 圖12 測試集4種模型股價預測趨勢比價
圖12 測試集4種模型股價預測趨勢比價
表5 模型RSME值
模型
移動平均
線性回歸
KNN
LSTM
RMSE
2.8579
1.7651
2.9326
0.4424
(因篇幅問題,另外三種模型的實現代碼沒有放出來,需要的可以私戳。)
綜合圖表結果分析得出,在准確率方面,LSTM表現最佳,其次是線性回歸,移動平均法和KNN算法模型表現最差;在預測未來股價的漲跌趨勢方面,移動平均和線性回歸的表現要稍微優於KNN,主要是因為他們消除了數據的波動性從而展示數據長期的趨勢。移動平均單純依靠前幾天的行情數據預測下一個交易日的股價,線性回歸和KNN依靠日期特征擬合回歸模型,傳統的線性模型和機器模型都不具有挖掘數據隱含信息的能力,在股票這種波動大、噪聲強的非線性數據上很難有令人滿意的表現。
而深度學習模型具備的一些特征使得他天生適合處理預測金融時序數據,如:1)深度學習模型不受維度限制,可以將所有與因變量相關的特征數據都納入模型當中,得到更完善的表征;2)具備很好的非線性擬合能力,適合擬合無規律波動大的時序數據;3)不容易陷入模型過擬合及局部最優;4)與線性回歸和傳統機器學習相比不需要人工手動的構造特征,通過多層神經網絡提取數據隱含特征,深度網絡表達能力更強等。且本文選取的LSTM網絡具備長期記憶的功能,對高噪聲的金融股票數據的預測效果會更好。
由於LSTM模型擬合效果很好,現使用LSTM模型預測未來短期內股價的走勢。考慮到周末深圳交易所休息,因此在預測時需要剔除雙休及節假日,本文中使用LSTM模型對未來30個工作日平安銀行的股價走勢進行預測,結果如下圖所示:
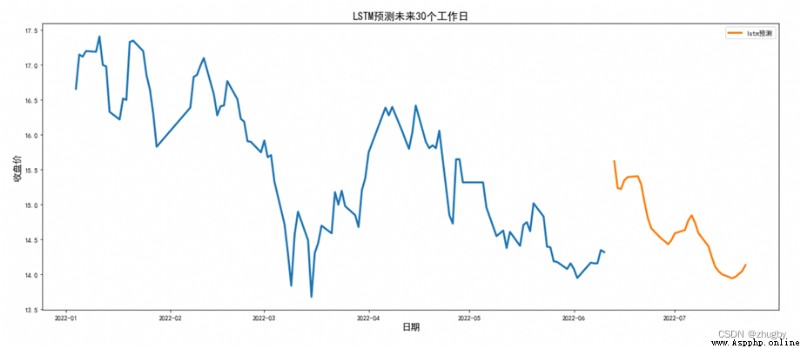
圖中存在中斷的一部分是因為我們真實的數據是截止2020-06-10,6月10日是周五,下一個工作日是6月12,因此預測日期中間會空出兩天,表現在圖形上就呈現出一小塊中斷。
觀察接下來一個月左右的股價走勢,未來一段時間總體上平安銀行的股價有下降的趨勢。投資者在6月10日周五時可以選擇加倉平安銀行的股票,在下一周股價上升到15.5左右的時候拋售留底,觀察股市動向,由於整體上下降趨勢,等到股市行情穩定之後可以考慮慢慢加倉。
值得注意的是,股價有可能會受到輿論、新聞媒體還有一些不可抗力的影響,比如大型自然災害、公司的費貨幣化合並拆分、公司名譽受損等等,這些無法提前預測的無形因素會對股價產生影響。因此,投資者不能完全依賴模型給出的預測結果,要多留意股市風向,謹慎投資。
1)實現提取剔除雙休的30天工作日日期:
import datetime
def date_by_adding_business_days(from_date, add_days):
business_days_to_add = add_days
current_date = from_date
re=[]
while business_days_to_add > 0:
current_date += datetime.timedelta(days=1)
current_date1=current_date.strftime("%Y-%m-%d")
weekday = current_date.weekday()
if weekday < 5: # sunday = 6
re.append(current_date1)
business_days_to_add -= 1
return re
data_pre=date_by_adding_business_days(datetime.date(2022, 6, 10), 30)2)模型預測:
dataset = new_data.values
train= dataset
#valid = dataset[2187:,:]
#converting dataset into x_train and y_train
scaler = MinMaxScaler(feature_range=(0, 1))
scaled_data = scaler.fit_transform(dataset)
x_train, y_train = [], []
for i in range(60,len(train)):
x_train.append(scaled_data[i-60:i,0])
y_train.append(scaled_data[i,0])
x_train, y_train = np.array(x_train), np.array(y_train)
x_train = np.reshape(x_train, (x_train.shape[0],x_train.shape[1],1))
model = Sequential()
model.add(LSTM(units=50, return_sequences=True, input_shape=(x_train.shape[1],1)))
model.add(LSTM(units=50))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
model.fit(x_train, y_train, epochs=1, batch_size=1, verbose=1)
#predicting 246 values, using past 60 from the train data
inputs = new_data[len(new_data) - 30 - 60:].values
inputs = inputs.reshape(-1,1)
inputs = scaler.transform(inputs)
X_test = []
for i in range(60,inputs.shape[0]):
X_test.append(inputs[i-60:i,0])
X_test = np.array(X_test)
X_test = np.reshape(X_test, (X_test.shape[0],X_test.shape[1],1))
closing_price = model.predict(X_test)
closing_price1 = scaler.inverse_transform(closing_price)
#rms=np.sqrt(np.mean(np.power((valid-closing_price1),2)))
#rms
lstm_pre['date']=data_pre
lstm_pre=pd.DataFrame()
lstm_pre['trade_date']=data_pre
lstm_pre['trade_date']=pd.to_datetime(lstm_pre['trade_date'], format="%Y-%m-%d")
lstm_pre['pred']=closing_price1
lstm_pre.index = lstm_pre['trade_date']
#lstm_pre.drop('trade_date', axis=1, inplace=True)
lstm_pre
#plot
train=new_data[2187:]
plt.figure(figsize=(20,8))
plt.plot(train['close'],linewidth=3)
plt.plot(lstm_pre['pred'],label='lstm預測',linewidth=3)
plt.title('LSTM預測未來30個工作日',fontsize=16)
plt.xlabel('日期',fontsize=14)
plt.ylabel('收盤價',fontsize=14)
plt.legend(loc=0)[1] Hochreiter, S, and J. Schmidhuber. “Long short-term memory.” Neural Computation 9.8(1997):1735-1780.
[2] 梁宇佳,宋東峰.基於LSTM和情感分析的股票預測[J].科技與創新,2021,(21):126-127.
[3]許雪晨,田侃.一種基於金融文本情感分析的股票指數預測新方法[J].數量經濟技術經濟研究,2021,38(12):124-145.DOI:10.13653/j.cnki.jqte.2021.12.009.