用動量和能量守恆計算圓周率

實現原理

靈感來自G. Galperin的論文PLAYING POOL WITH π (THE NUMBER π FROM A BILLIARD POINT OF VIEW)，DOI: 10.1070/RD2003v008n04ABEH000252。我在這裡只是簡單介紹下原理，感興趣的同學們可以自己仔細閱讀。論文是全英文，有需要可以私信我，有問題我幫你解答。Youtube上3Blue1Brown的視頻有介紹這片論文，有很好的圖片和講解，更好理解。

簡單概括下，Galperin的想法很神奇。不同於普通的算π的方法（如無限級數法），作者用動量守恆和動能守恆算 π π π！

首先，我們來理解一下動量守恆和能量守恆。
在完全彈性碰撞中，兩個物體在碰撞後除了動能的轉換沒有其它能量的消耗。這是完全彈性碰撞的動量守恆公式：
m 1 v 1 + m 2 v 2 = m 1 v 1 ′ + m 2 v 2 ′ m_{1}v_{1}+m_{2}v_{2}=m_{1}v_{1}^{'}+m_{2}v_{2}^{'} m1​v1​+m2​v2​=m1​v1′​+m2​v2′​

基於此，二者能量的關系可用動能守恆表示：
1 2 m 1 v 1 2 + 1 2 m 2 v 2 2 = 1 2 m 1 v 1 ′ 2 + 1 2 m 2 v 2 ′ 2 \frac{1}{2}m_{1}v_{1}^{2}+\frac{1}{2}m_{2}v_{2}^{2}=\frac{1}{2}m_{1}v_{1}^{'2}+\frac{1}{2}m_{2}v_{2}^{'2} 21​m1​v12​+21​m2​v22​=21​m1​v1′2​+21​m2​v2′2​
連立上面兩條公式，我們得到：
{ m 1 v 1 + m 2 v 2 = m 1 v 1 ′ + m 2 v 2 ′ 1 2 m 1 v 1 2 + 1 2 m 2 v 2 2 = 1 2 m 1 v 1 ′ 2 + 1 2 m 2 v 2 ′ 2 \left\{ \begin{array}{lr} m_{1}v_{1}+m_{2}v_{2}=m_{1}v_{1}^{'}+m_{2}v_{2}^{'} & \\ \\ \frac{1}{2}m_{1}v_{1}^{2}+\frac{1}{2}m_{2}v_{2}^{2}=\frac{1} {2}m_{1}v_{1}^{'2}+\frac{1}{2}m_{2}v_{2}^{'2} & \end{array} \right. ⎩⎨⎧​m1​v1​+m2​v2​=m1​v1′​+m2​v2′​21​m1​v12​+21​m2​v22​=21​m1​v1′2​+21​m2​v2′2​​​
化簡該公式，我們得到：
{ v 1 ′ = ( m 1 − m 2 ) v 1 + 2 m 2 v 2 m 1 + m 2 v 2 ′ = ( m 2 − m 1 ) v 2 + 2 m 1 v 1 m 1 + m 2 \left\{ \begin{array}{lr} v_{1}^{'}=\frac{(m_{1}-m_{2})v_{1}+2m_{2}v_{2}}{m_{1}+m_{2}} & \\ \\ v_{2}^{'}=\frac{(m_{2}-m_{1})v_{2}+2m_{1}v_{1}}{m_{1}+m_{2}} & \end{array} \right. ⎩⎪⎨⎪⎧​v1′​=m1​+m2​(m1​−m2​)v1​+2m2​v2​​v2′​=m1​+m2​(m2​−m1​)v2​+2m1​v1​​​​
這樣，我們就有了程序模擬的核心算法。

在下圖所示的理想的物理系統（無摩擦力，牆和地面質量無限，球體無角動量等）中，這兩條關系成立：（圖源：Galperin）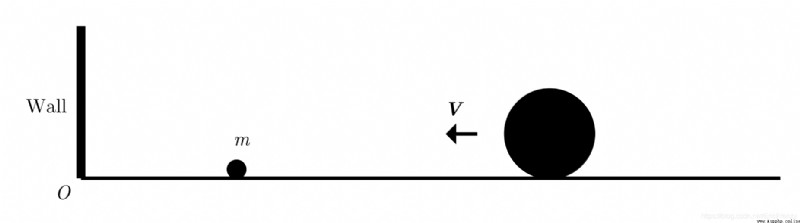

具體的數學證明，Galperin在論文中有提到。我們要做的，就是用暴力模擬驗證他的結論。設物體朝牆運動時速度為正，遠離牆時速度為負。二者的碰撞在以下情況時： 0 > v 2 ≥ v 1 0>v_{2}\geq v_{1} 0>v2​≥v1​，兩個物體不會再次相遇。

Galperin的數學論證非常詳盡。總而言之，他證明了以下關系：
Π ( N ) = 314159265358979... Π(Ν)=314159265358979... Π(N)=314159265358979...
其中 Π ( N ) Π(Ν) Π(N)是當大物體重量是小物體的 10 0 N 100^Ν 100N倍時的碰撞次數， N N N是計算 π π π的位數-1。
我們要做的，就是根據他的論文寫個程序實現。

代碼

#!/usr/local/bin/python3
import time
from decimal import *
from decimal import Decimal as dcm #這個庫提高下浮點運算精度
getcontext().prec = 50 #小數位數設為50位
N = int(input("Enter N:"))
m = dcm(1) #初始化m1
M = dcm(m*100**N) #初始化m2
vm0 = dcm(0) #初始化v1
vM0 = dcm(10000) #初始化v2
vm = vm0 #初始化v1'
vM = vM0 #初始化v2'
cnt = -3 #初始化計數器 經過測試軟件總會多算幾次 所以先-3
start = time.time() #設置一個計時器，算所需時間
while not (vm < vM and vM < dcm(0)): #也就是當兩個物體不會同時向右且不再相遇時
vm = dcm((m-M)*vm0+2*M*vM0)/dcm(M+m)
vM = dcm((M-m)*vM0+2*m*vm0)/dcm(M+m) #上面提到的兩個核心模擬算法
cnt += 1
vm0 = dcm(-vm) #彈性碰撞，小物體的動量變成反方向
vM0 = dcm(vM) #大物體動量更新，方向不變
cnt += 1 #又撞了一次
end = time.time() #結束計時器
print("Number of collisions:", cnt)
print("Time elapse:", end-start, "seconds.") #輸出

運行結果

運行結果見下表：（本人自制）
最左第一列是N的值
第二列是輸出的碰撞次數
第三列是運行時間
第四列是根據輸出計算的 π π π值
第五列是和真實 π π π值的差距

下圖是N的變化與計算偏差的指數回歸：（作者自制）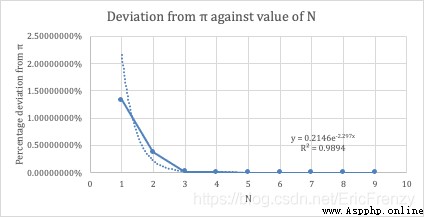

由上圖可見，隨著N的增大，計算的圓周率指數級地無限趨於准確。

下圖是N的變化與計算所需時間的指數回歸：（作者自制）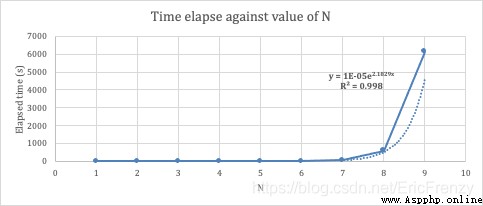

可見，隨著准確度的指數級提高，計算的時間復雜度也指數級地提高。因此，一般的筆記本真算不過來太大的N。

總結與拓展

我們的程序確實非常有效。然而，有很多其它計算 π π π的方法更加高效。我們的程序也有一些疏漏。比如，輸出的值永遠是奇數。這是因為在while循環裡默認最小增加值是2。有興趣的小伙伴可以思考下如何解決！也許可以多加幾個判定？
對於Galperin論文感興趣的同學請私信我或留評論，我會很樂意幫助你們解答相關問題！

ps：本人在用這些東西寫小論文，所以轉載請引用！