線性表的鏈式存儲結構稱為鏈表。在鏈表中每個結點不僅包含元素本身的信息,還包含元素之間邏輯關系的信息,即一個結點中包含後繼結點的地址信息或者前驅結點的地址信息,稱為指針屬性。這樣將可以通過一個結點的指針屬性方便地找到後繼結點或前驅結點。
如果每個結點只設置一個指向其後繼結點的指針屬性,這樣的鏈表稱為單(向)鏈表。如果每個結點設置兩個指針屬性,分別用於指向其前驅結點和後繼結點,這樣的鏈表稱為雙(向)鏈表。如下圖所示:


無前驅結點或者後繼結點的相應指針屬性用 None 表示。
為了便於在鏈表中插入和刪除結點,通常鏈表帶有一個頭結點,並通過頭結點指針唯一標識該鏈表。
通常將 p p p 指向的結點稱為 p p p 結點或結點 p p p,頭結點為 head 的鏈表稱為 head 鏈表。頭結點中不存放任何數據元素(空表是僅包含頭結點的鏈表)。一般鏈表的長度不計頭結點,僅指其中數據結點的個數。
為實現單鏈表,我們需要創建鏈表結點類與鏈表類,如下:
class LinkNode:
def __init__(self, data=None):
self.data = data # 存放數據,默認為None,即沒有數據
self.next = None # 指針,用於指向下一個結點
class LinkList:
def __init__(self):
self.head = LinkNode() # 頭結點不包含數據,因此不傳入參數
self.head.next = None # 初始化鏈表時,得到的是空鏈表
該方法從一個空表開始,不斷讀取數組 a a a 中的元素並生成新結點 s s s,再將 s s s 插入到鏈表的表頭處。
def fromlist(self, a):
for i in range(len(a)):
s = LinkNode(a[i])
s.next = self.head.next
self.head.next = s
時間復雜度 O ( n ) \mathcal{O}(n) O(n), n n n 為 a a a 中元素的個數。
顯而易見,采用頭插法建立出來的鏈表,其數據次序與 a a a 中的次序完全相反。
若希望鏈表中的數據次序與原數組保持一致,可采用尾插法。為此需要增加一個尾指針 t t t,使其始終指向當前鏈表的尾結點。
def fromlist(self, a):
t = self.head
for i in range(len(a)):
s = LinkNode(a[i])
t.next = s
t = s
t.next = None
時間復雜度 O ( n ) \mathcal{O}(n) O(n)。
為在單鏈表中實現線性表的相關運算,我們首先需要實現一個功能,即查找序號為 i i i 的結點。
def geti(self, i):
p = self.head # 從頭結點開始遍歷
j = -1 # 因為頭結點指向的下一個結點的索引是0
while j < i and p is not None:
p = p.next
j += 1
return p
時間復雜度 O ( n ) \mathcal{O}(n) O(n)。
def add(self, e):
p = self.head
s = LinkNode(e)
while p.next is not None:
p = p.next
p.next = s
時間復雜度 O ( n ) \mathcal{O}(n) O(n)。
插入元素遵循以下步驟:
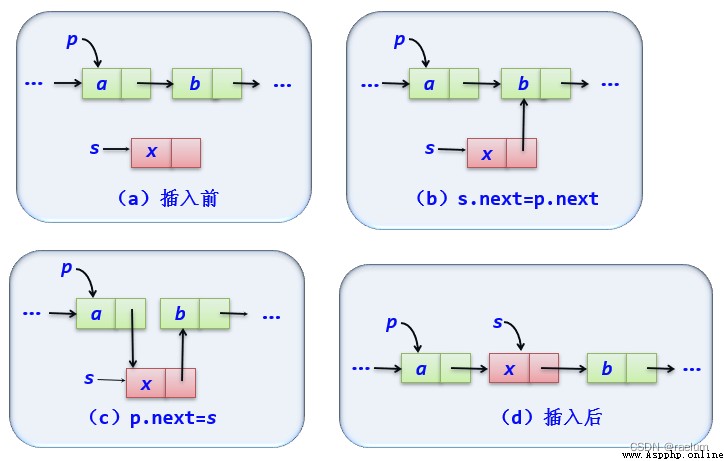
def insert(self, i, e):
assert i >= 0
p = self.geti(i - 1)
assert p is not None
s = LinkNode(e)
s.next = p.next
p.next = s
時間復雜度 O ( n ) \mathcal{O}(n) O(n)。
刪除元素遵循以下步驟:
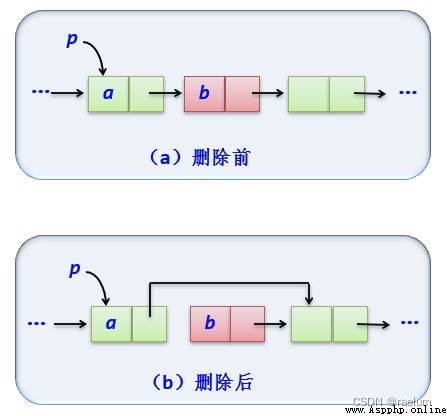
def delete(self, i):
assert i >= 0
p = self.geti(i - 1)
assert p is not None and p.next is not None
p.next = p.next.next
時間復雜度 O ( n ) \mathcal{O}(n) O(n)。
def __getitem__(self, i):
assert i >= 0
p = self.geti(i)
assert p is not None
return p.data
時間復雜度 O ( n ) \mathcal{O}(n) O(n)。
def __setitem__(self, i, x):
assert i >= 0
p = self.geti(i)
assert p is not None
p.data = x
時間復雜度 O ( n ) \mathcal{O}(n) O(n)。
def getno(self, e):
p = self.head.next
k = 0
while p is not None and p.data != e:
p = p.next
k += 1
return -1 if p is None else k # 未找到時返回-1
時間復雜度 O ( n ) \mathcal{O}(n) O(n)。
def getsize(self):
p = self.head.next
j = 1
while p.next is not None:
p = p.next
j += 1
return j
時間復雜度 O ( n ) \mathcal{O}(n) O(n)。
打印單鏈表即打印其中的所有數據元素。
def display(self):
p = self.head.next
while p.next is not None:
print(p.data, end=' ')
p = p.next
print(p.data)
這種打印方式可保證最後一個數字後面的字符不是空格而是換行符。
與單鏈表類似:
class DLinkNode:
def __init__(self, data=None):
self.data = data
self.prior = None
self.next = None
class DLinkList:
def __init__(self):
self.dhead = DLinkNode()
self.dhead.prior = None
self.dhead.next = None
和單鏈表一樣,雙鏈表也是由頭結點 head 唯一標識的。
def fromlist(self, a):
for i in range(len(a)):
s = DLinkList(a[i])
# 先建立s與其下一個結點的雙向關系
s.next = self.dhead.next
if self.dhead.next is not None:
self.dhead.next.prior = s
# 再建立s與其上一個結點的雙向關系
self.dhead.next = s
s.prior = self.dhead
def fromlist(self, a):
t = self.dhead
for i in range(len(a)):
s = DLinkList(a[i])
# 建立s與鏈表尾結點的雙向關系
t.next = s
s.prior = t
# 移動指針
t = s
t.next = None
與單鏈表類似:
def insert(self, i, e):
assert i >= 0
p = self.geti(i - 1)
assert p is not None
s = DLinkNode(e)
s.next = p.next
if p.next is not None:
p.next.prior = s
p.next = s
s.prior = p
與單鏈表類似:
def delete(self, i):
assert i >= 0
p = self.geti(i)
assert p is not None
p.prior.next = p.next
if p.next is not None:
p.next.prior = p.prior
循環單鏈表的尾結點的指針屬性不再是 None,而是指向頭結點:
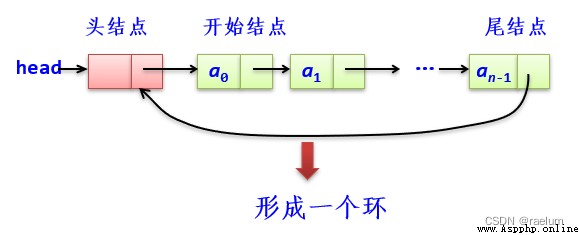
循環單鏈表的特點是從表中任一結點出發都可以找到其他結點。與單鏈表相比,無需增加存儲空間,僅對鏈接方式稍作修改,即可使得表處理更加方便、靈活。
循環單鏈表中的結點類型與非循環單鏈表中的結點類型相同,仍為 LinkNode。
class CLinkList:
def __init__(self):
self.head = LinkNode()
self.head.next = self.head # 因為初始時鏈表是空的,所以頭結點指向頭結點
循環單鏈表的插入和刪除結點操作與非循環單鏈表的相同,所以兩者的許多基本運算算法是相似的,主要區別如下:
head,在循環單鏈表的構造方法中需要通過 head.next = head 語句設置空表;p.next == head 而不是 p.next == None。循環雙鏈表的尾結點的 next 指針指向頭結點,頭結點的 prior 指針指向尾結點:
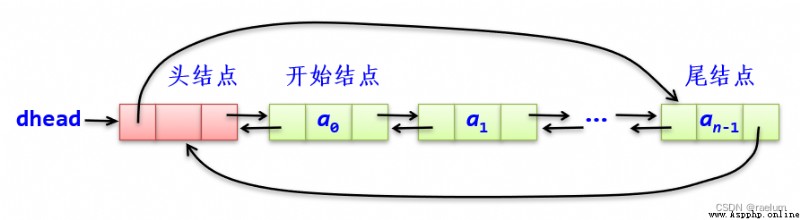
其特點是整個鏈表形成兩個環,由此從表中任一結點出發均可找到其他結點,最突出的優點是通過頭結點在 O ( 1 ) \mathcal{O}(1) O(1) 時間內找到尾結點。
循環雙鏈表中的結點類型與非循環雙鏈表中的結點類型相同,仍為 DLinkNode。
class CDLinkList:
def __init__(self):
self.dhead = DLinkNode()
self.dhead.next = self.dhead
self.dhead.prior = self.dhead
對於一種存儲結構,定義其存儲密度:
存 儲 密 度 = 結點中數據本身占用的存儲量 整個結點占用的存儲量 存儲密度=\frac{\text{結點中數據本身占用的存儲量}}{\text{整個結點占用的存儲量}} 存儲密度=整個結點占用的存儲量結點中數據本身占用的存儲量
一般地,存儲密度越大,存儲空間的利用率就越高。
顯然,順序表的存儲密度為1,而鏈表的存儲密度小於1。僅從存儲密度看,順序表的存儲空間利用率更高。
此外,順序表需要預先分配空間,如果空間過小會出現上溢出,如果空間過大會導致內存浪費。而鏈表的存儲空間是動態分配的,只要內存足夠,就不會出現上溢出。
所以,
從查找操作來看,順序表具有隨機存儲特性,給定序號查找指定元素的時間為 O ( 1 ) \mathcal{O}(1) O(1);而鏈表不具有隨機存儲特性,只能順序訪問,給定序號查找指定元素的時間為 O ( n ) \mathcal{O}(n) O(n)。
從插入和刪除操作來看,在順序表中執行該操作通常需要移動半個表的元素;而在鏈表中執行該操作僅需要修改相關結點的指針屬性,不必移動結點。
所以,
LeetCode中的單鏈表結點定義為:
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
以下所有代碼均通過測試。

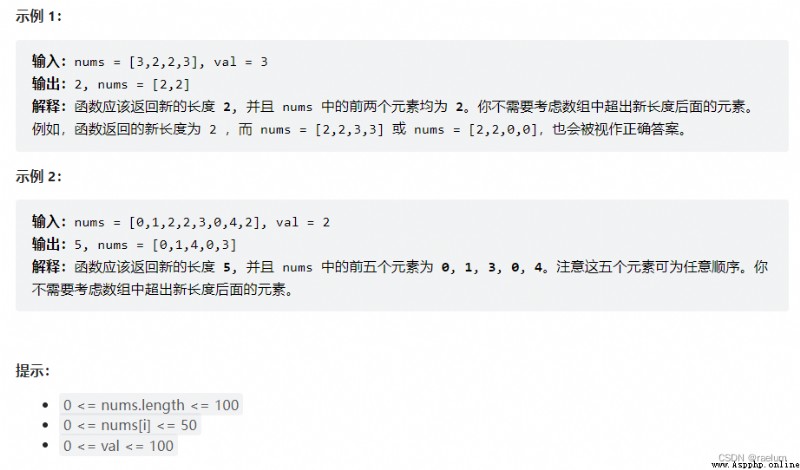
本題LeetCode會自動追蹤
nums,因此只需返回整數。
我們可以設置兩個指針:left 和 right。其中右指針指向當前要處理的元素,左指針指向下一個將要賦值的位置。
如果右指針指向的元素等於 val,則此時左指針不動,右指針右移一位。否則,將右指針指向的元素復制到左指針的位置,然後將左右指針同時右移一位。
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
left = 0
for right in range(len(nums)):
if nums[right] != val:
nums[left] = nums[right]
left += 1
return left
注意到該算法在最壞的情況下,即 nums 中不含 val,左右指針均要遍歷一次數組,即總共遍歷了兩次。此外,該算法會對要保留的元素進行重復賦值(當 left = right 時)。
復雜度分析
考慮初始時將左右指針分別置於數組的兩端。
當左指針指向 val 時,此時將右指針指向的元素復制到左指針處,同時將右指針左移一位。如果復制過來的元素恰好也是 val,則繼續執行上述操作直至左指針指向的不是 val。
當左指針指向的不是 val 時,將左指針右移一位。
當左右指針重合時,左右指針一起遍歷了整個數組。
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
left, right = 0, len(nums) - 1
while left <= right:
if nums[left] == val:
nums[left] = nums[right]
right -= 1
else:
left += 1
return left
復雜度分析
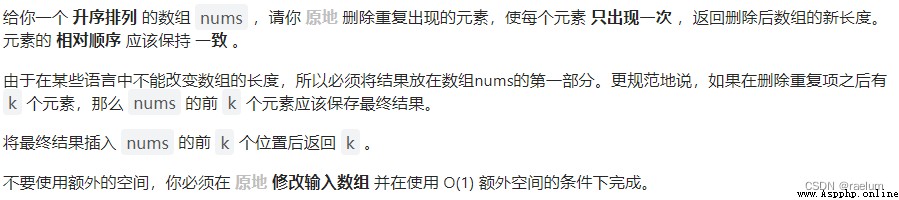
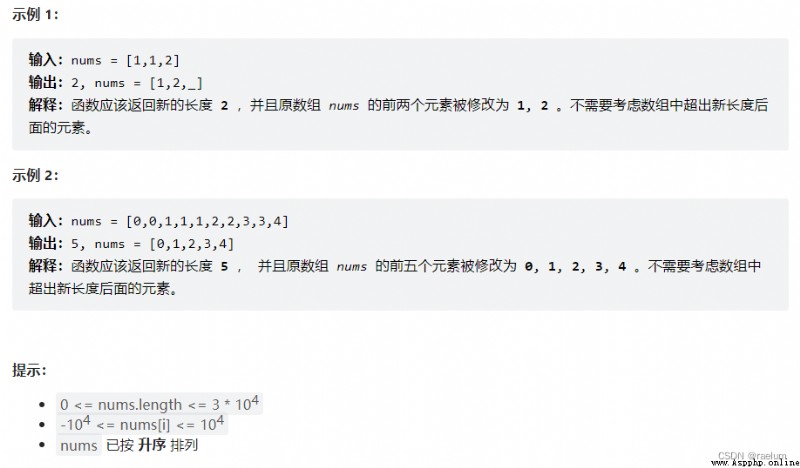
從有序可以得知,重復項一定是連在一起的。此外,由於本題未給定 val,所以可能會有多種重復元。
具體來說,設置兩個左右指針,初始時均位於數組左端。當右指針指向的元素和左指針相同時,右指針右移一位。若不同,則先將左指針右移一位,再將右指針指向的值復制到左指針處。
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
left = 0
for right in range(len(nums)):
if nums[left] != nums[right]:
left += 1
nums[left] = nums[right]
return left + 1

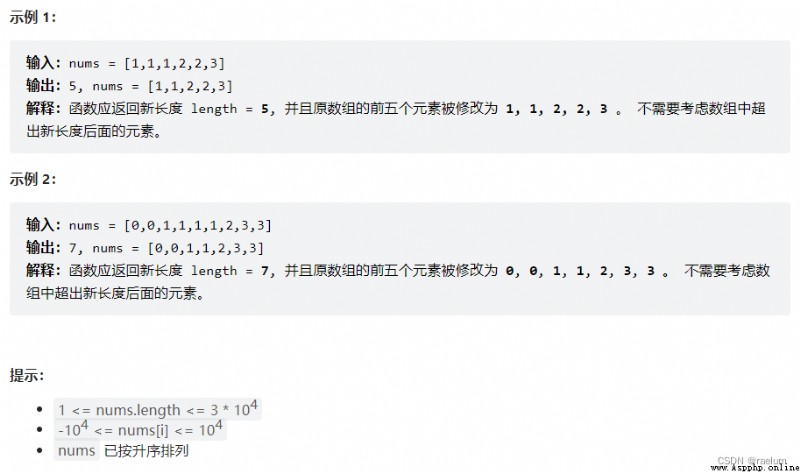
我們采用快慢指針解法。其中慢指針表示處理出的數組的長度,快指針表示已經檢查過的數組的長度。
初始時置快慢指針均在數組左端,且應保留數組的前兩個數字。因此起初應讓快慢指針同步移動到索引 2 2 2 處且不做任何修改。因為同一元素最多出現兩次,所以比較 nums[slow - 2] 和 nums[fast],當它們相同時,只讓快指針右移一位;當它們不同時,將快指針指向的值復制到左指針處,然後讓左右指針均右移一位。
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
slow = 0
for fast in range(len(nums)):
if slow < 2 or nums[slow - 2] != nums[fast]:
nums[slow] = nums[fast]
slow += 1
return slow


擺爛解法:
class Solution:
def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
nums = sorted(nums1 + nums2)
n = len(nums)
if n % 2 != 0:
return nums[n // 2]
else:
return (nums[n // 2 - 1] + nums[n // 2]) / 2
因為調用了 sorted 函數,所以時間復雜度是 O ( ( m + n ) log ( m + n ) ) \mathcal{O}((m+n)\log(m+n)) O((m+n)log(m+n))。所以雖然上述代碼能夠成功運行,但並不符合題目要求。
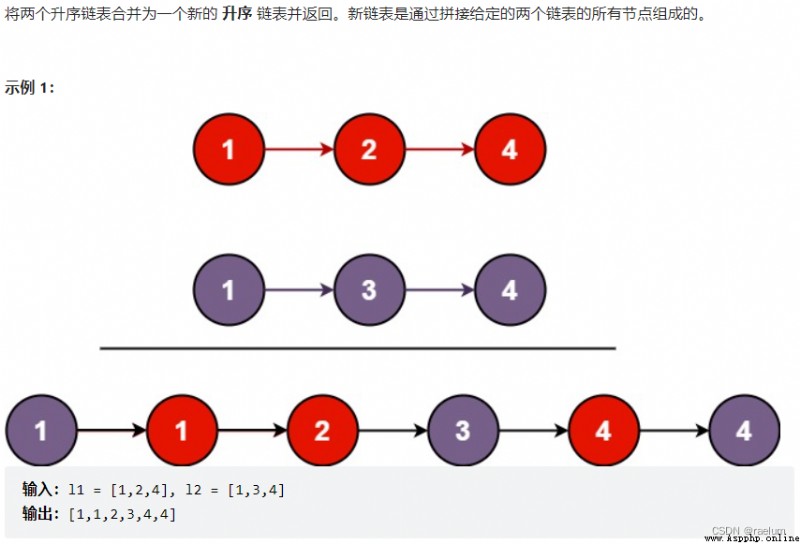

首先設定一個哨兵結點 sentinel,這可以在最後讓我們比較容易地返回合並後的鏈表。我們設置三個指針 l1、l2 和 prev,l1 和 l2 分別遍歷 list1 和 list2。初始時 prev 指向哨兵結點。
當 l1 小於 l2 時,我們將 l1 指向的結點接在 prev 後,然後將 prev 和 l1 均後移一位。否則,我們將 l2 指向的結點接在 prev 後,然後將 prev 和 l2 均後移一位。
循環終止的時候,l1 和 l2 至多有一個是非空的,由於輸入的兩個鏈表都是有序的,所以我們只需要簡單地將非空鏈表接在合並鏈表的後面,並返回合並鏈表即可。
class Solution:
def mergeTwoLists(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:
sentinel = ListNode(-1)
prev = sentinel
while l1 and l2:
if l1.val < l2.val:
prev.next = l1
l1 = l1.next
else:
prev.next = l2
l2 = l2.next
prev = prev.next
prev.next = l2 if l1 is None else l1
return sentinel.next
時間復雜度: O ( m + n ) \mathcal{O}(m+n) O(m+n),空間復雜度: O ( 1 ) \mathcal{O}(1) O(1)。
class Solution:
def mergeTwoLists(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:
# 邊界條件
if l1 is None:
return l2
if l2 is None:
return l1
# 遞歸主體
if l1.val < l2.val:
l1.next = self.mergeTwoLists(l1.next, l2)
return l1
else:
l2.next = self.mergeTwoLists(l1, l2.next)
return l2
時間復雜度: O ( m + n ) \mathcal{O}(m+n) O(m+n),空間復雜度: O ( m + n ) \mathcal{O}(m+n) O(m+n)。
遞歸調用
mergeTwoLists函數時需要消耗棧空間,棧空間的大小取決於遞歸調用的深度。結束遞歸調用時mergeTwoLists函數最多調用 n + m n+m n+m 次,因此空間復雜度為 O ( n + m ) \mathcal{O}(n+m) O(n+m)。

class Solution:
def deleteDuplicates(self, head: ListNode) -> ListNode:
if not head:
return head
cur = head
while cur.next:
if cur.val == cur.next.val:
cur.next = cur.next.next
else:
cur = cur.next
return head
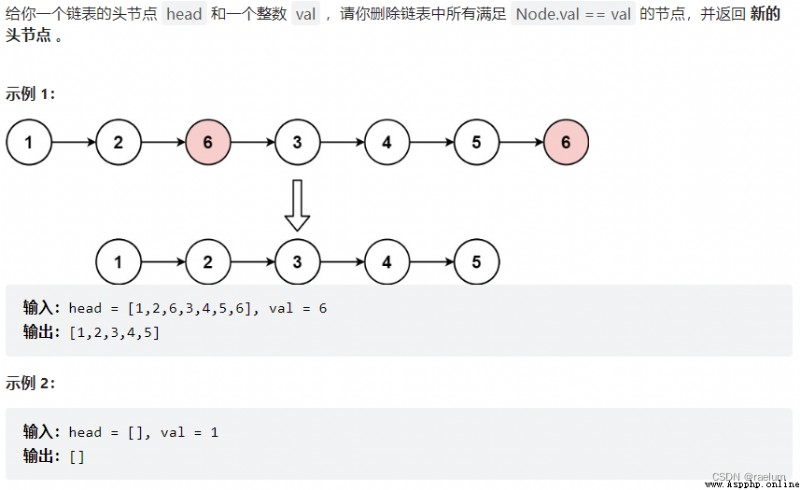

因為頭結點可能會變動,所以我們依然使用哨兵結點的方法。此外,設置一個指針 cur 用來遍歷整個列表。
class Solution:
def removeElements(self, head: ListNode, val: int) -> ListNode:
if not head: return head
sentinel = ListNode(-1)
sentinel.next = head
cur = sentinel
while cur.next:
if cur.next.val == val:
cur.next = cur.next.next
else:
cur = cur.next
return sentinel.next
本題依然可以采用遞歸的方法。
class Solution:
def removeElements(self, head: ListNode, val: int) -> ListNode:
if not head: return head
head.next = self.removeElements(head.next, val)
# 如果head本身就需要刪除,則返回head的下一個結點,否則返回head本身
return head.next if head.val == val else head
首先最容易想到的方法就是兩次遍歷。第一次遍歷計算鏈表的總長度,第二次遍歷確定要刪除的結點。該方法過於簡單粗暴所以這裡不再介紹。
對於本題,我們可以設置一個快慢指針,想辦法讓快指針走到鏈表末尾時,慢指針剛好位於倒數第 n + 1 n+1 n+1 個結點。
class Solution:
def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
sentinel = ListNode(-1, head)
slow, fast = sentinel, head
for _ in range(n):
fast = fast.next
while fast:
fast = fast.next
slow = slow.next
slow.next = slow.next.next
return sentinel.next
最粗暴的方法就是將鏈表的值依次存儲到一個列表 nums 中,然後通過 nums==nums[::-1] 來判斷所給鏈表是不是回文鏈表。
另外一種思路是將鏈表的前半部分依次壓入棧中,然後再將棧中元素依次彈出並與鏈表的後半部分比較。此方法需要考慮鏈表長度的奇偶性。
以上兩種方法的空間復雜度均為 O ( n ) \mathcal{O}(n) O(n),下面提供一種 O ( 1 ) \mathcal{O}(1) O(1) 的解決方案——快慢指針法。
整個流程分為以下幾個步驟:
class Solution:
def isPalindrome(self, head: ListNode) -> bool:
if not head: return True
first_half_end = self.get_middle_position(head)
second_half_start = self.reverse_list(first_half_end.next)
flag = True
left, right = head, second_half_start
while flag and right:
if left.val != right.val:
flag = False
left = left.next
right = right.next
return flag
def get_middle_position(self, head):
slow, fast = head, head
while fast.next and fast.next.next:
slow = slow.next
fast = fast.next.next
return slow
def reverse_list(self, head):
prev, cur = None, head
while cur:
next_node = cur.next
cur.next = prev
prev = cur
cur = next_node
return prev
嚴謹來講,我們還應在判斷完後恢復鏈表。


可先將鏈表構成循環鏈表,然後再將指定的位置切開。
class Solution:
def rotateRight(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:
if not head: return head
# 構成循環鏈表並計算鏈表長度
p = head
length = 1
while p.next:
p = p.next
length += 1
p.next = head
# 斷開鏈接
pos = length - k % length
p = head
k = 1
while k < pos:
p = p.next
k += 1
next_node = p.next
p.next = None
return next_node
class LinkNode:
def __init__(self, data=None):
self.data = data
self.next = None
class LinkList:
def __init__(self):
self.head = LinkNode()
self.head.next = None
def fromlist(self, a):
t = self.head
for i in range(len(a)):
s = LinkNode(a[i])
t.next = s
t = s
t.next = None
def geti(self, i):
p = self.head
j = -1
while j < i and p is not None:
p = p.next
j += 1
return p
def add(self, e):
p = self.head
s = LinkNode(e)
while p.next is not None:
p = p.next
p.next = s
def insert(self, i, e):
assert i >= 0
p = self.geti(i - 1)
assert p is not None
s = LinkNode(e)
s.next = p.next
p.next = s
def delete(self, i):
assert i >= 0
p = self.geti(i - 1)
assert p is not None and p.next is not None
p.next = p.next.next
def __getitem__(self, i):
assert i >= 0
p = self.geti(i)
assert p is not None
return p.data
def __setitem__(self, i, x):
assert i >= 0
p = self.geti(i)
assert p is not None
p.data = x
def getno(self, e):
p = self.head.next
k = 0
while p is not None and p.data != e:
p = p.next
k += 1
return -1 if p is None else k
def getsize(self):
p = self.head.next
j = 1
while p.next is not None:
p = p.next
j += 1
return j
def display(self):
p = self.head.next
while p.next is not None:
print(p.data, end=' ')
p = p.next
print(p.data)
class DLinkNode:
def __init__(self, data=None):
self.data = data
self.prior = None
self.next = None
class DLinkList:
def __init__(self):
self.dhead = DLinkNode()
self.dhead.prior = None
self.dhead.next = None
def fromlist(self, a):
t = self.dhead
for i in range(len(a)):
s = DLinkList(a[i])
# 建立s與鏈表尾結點的雙向關系
t.next = s
s.prior = t
# 移動指針
t = s
t.next = None
def geti(self, i):
p = self.dhead
j = -1
while j < i and p is not None:
p = p.next
j += 1
return p
def insert(self, i, e):
assert i >= 0
p = self.geti(i - 1)
assert p is not None
s = DLinkNode(e)
s.next = p.next
if p.next is not None:
p.next.prior = s
p.next = s
s.prior = p
def delete(self, i):
assert i >= 0
p = self.geti(i)
assert p is not None
p.prior.next = p.next
if p.next is not None:
p.next.prior = p.prior