Queues are Operations Limited The linear table , It is limited to allowing insertion only at one end of the table , Delete at the other end of the table . The end of the insertion is called A party (rear), The end of deletion is called Team head or Team leader (front). Inserting elements into a queue is called Enter the team or The team , Deleting an element from a queue is called Out of the team or Leave the team .
A distinguishing feature of queues is :FIFO(First In First Out).
Queues need to be implemented in the same way as stacks :empty()、push(e)、pop() and gethead().
The queue with sequential storage structure is called Sequential team . We use lists data To store the elements in the queue , Set two more pointers , The team head pointer is front, The tail pointer is rear.
For the sake of simplicity , Here is a list of fixed capacities :

front Pointing to the team head element Previous Location , and rear Just right Point to the end element .
The sequential team is divided into Acyclic queues and Circular queue Two structures , Let's first discuss acyclic queues , And by explaining the shortcomings of this type of queue, it leads to the circular queue .
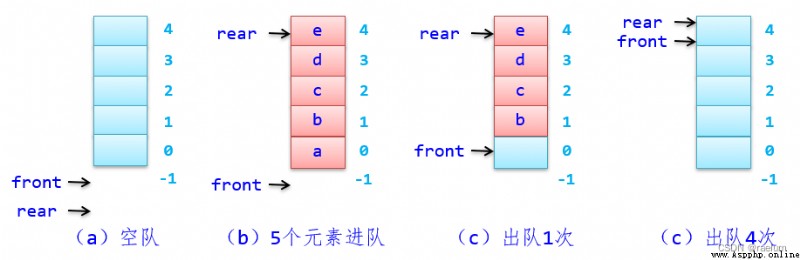
Initial time setting front and read Are all -1, The four elements of an acyclic queue are as follows :
front == rear;rear = MaxSize - 1;rear increase 1, And will e e e Put it in that position ( The elements that enter the team are always inserted at the end );front increase 1, Take out the element in this position ( The element of leaving the team always comes out at the head of the team ).The structure of acyclic queue is as follows :
class SqQueue:
def __init__(self):
self.__MaxSize = 100
self.data = [None] * self.__MaxSize
self.front = self.rear = -1
Complete implementation :
class SqQueue:
def __init__(self):
self.__MaxSize = 100
self.data = [None] * self.__MaxSize
self.front = self.rear = -1
def empty(self):
return self.front == self.rear
def push(self, e):
assert self.rear != self.__MaxSize - 1
self.rear += 1
self.data[self.rear] = e
def pop(self):
assert not self.empty()
self.front += 1
return self.data[self.front]
def gethead(self):
assert not self.empty()
return self.data[self.front + 1]
The time complexity of the above operations is O ( 1 ) \mathcal{O}(1) O(1).
In an acyclic queue , When the element enters the team, the pointer at the end of the team rear += 1, When elements are out of the team front += 1. When the team is full , namely rear = MaxSize - 1 When established , At this time, even if there are still several elements in the team , All that changed was front The location of , and rear unchanged , Even if the team meets the conditions, it still holds . This kind of up overflow with empty positions in the queue but still meeting the condition of full queue is called False spillover . in other words , There is a false overflow phenomenon in the acyclic queue .
In order to overcome false overflow , Make full use of the storage space of the array , We can data Connect the front and back ends of the array , Form a circular array , That is, the table storing queue elements is logically regarded as a ring , be called Circular queue .
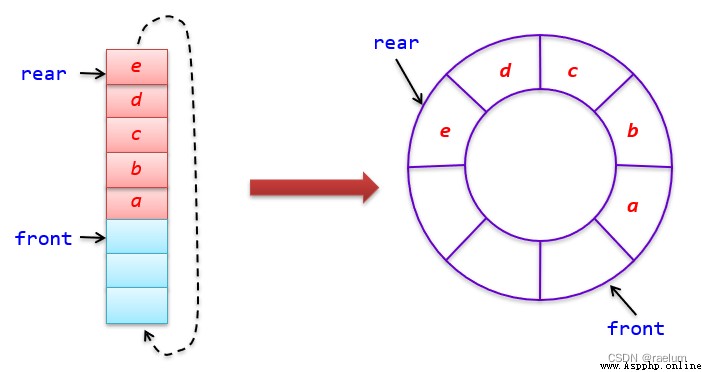
The circular queue is end-to-end , When the tail pointer rear = MaxSize - 1 when , One more position and you'll arrive 0, This can be achieved by using the remainder operation :
The queue head pointer and queue tail pointer of the circular queue initially point to 0( The real location , Unlike the acyclic queue, the queue head pointer and the queue tail pointer initially point to the virtual location -1). When there are elements in the team ,rear += 1, When there are elements out of the team ,front += 1.
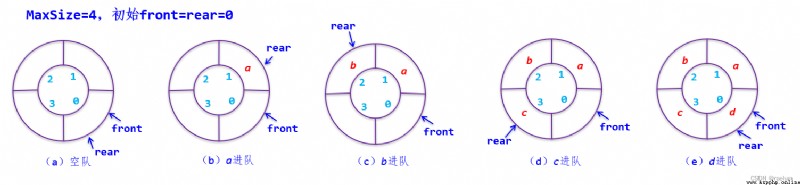
A detail can be found from the above figure : When the team is empty and full rear == front, Then how should we judge the team's empty ? In fact, we need to add one constraint , As follows .
Both circular queues and acyclic queues need to pass front and rear To identify the queue status . We know , A length of m m m There are the following queues m + 1 m+1 m+1 States :
If taken |front - rear| To identify the status of the circular queue , because front and rear The value range of is 0 ∼ m − 1 0\sim m-1 0∼m−1, thus |front - rear| Only m m m Species value . be aware m < m + 1 m<m+1 m<m+1, So if you use |front - rear| To distinguish the queue status , There must be Two kinds of Status cannot be distinguished . So if we limit the length to m m m The queue of contains at most m − 1 m-1 m−1 One element , You can use |front - rear| To distinguish all queue States .
Why are there two states that cannot be distinguished instead of one ? We can consider the simplest case , Suppose the queue length is 1 1 1, So there are only two states : Team space , There is only one element in the team ( That is, the team is full ). here
|front - rear|There is only one value : 0 0 0, We cannot judge the specific status of the queue by this value .
It is specified that the circular queue can contain at most m − 1 m-1 m−1 After elements , We can use rear == front To judge that the team is empty . When the team is full ( That is, the queue contains m − 1 m-1 m−1 Elements ), There must be (rear + 1) % MaxSize == front. So we get the four elements of the circular queue :
rear == front;(rear + 1) % MaxSize == front;rear = (rear + 1) % MaxSize, then e e e Put it in that position ;front = (front + 1) % MaxSize, Take out the element in this position .The complete implementation is as follows :
class CSqQueue:
def __init__(self):
self.__MaxSize = 100
self.data = [None] * self.__MaxSize
self.front = self.rear = 0
def empty(self):
return self.front == self.rear
def push(self, e):
assert (self.rear + 1) % self.__MaxSize != self.front
self.rear = (self.rear + 1) % self.__MaxSize
self.data[self.rear] = e
def pop(self):
assert not self.empty()
self.front = (self.front + 1) % self.__MaxSize
return self.data[self.front]
def gethead(self):
assert not self.empty()
return self.data[(self.front + 1) % self.__MaxSize]
The time complexity of the above operations is O ( 1 ) \mathcal{O}(1) O(1).
The chained storage structure of queues is abbreviated as The chain team . It is realized by a single linked list composed of nodes . At this time, only the header of the single linked list can be deleted , Insert at the end of the single linked list .
It should be noted that , The single linked list here does not take the lead , And you need two pointers to identify the single linked list . among front Point to the head of the team ,rear Point to the end of the line .
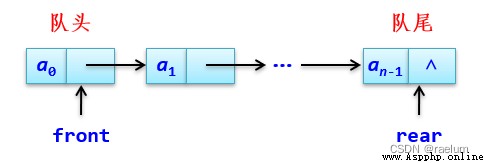
The basic structure is as follows :
class LinkNode:
def __init__(self, data=None, next=None):
self.data = data
self.next = next
class LinkQueue:
def __init__(self):
self.front = None
self.rear = None
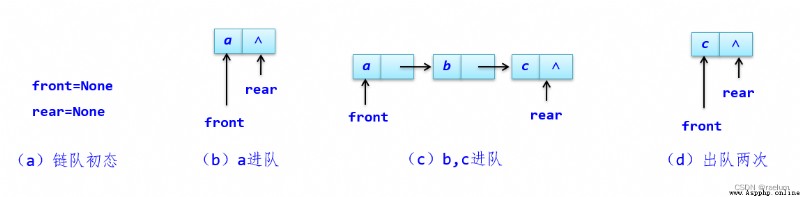
The four elements of the chain team are as follows :
front == rear == None, Just front == None As a team air condition ;rear Pointing to it ;data Value and delete it from the chain .class LinkQueue:
def __init__(self):
self.front = None
self.rear = None
def empty(self):
return self.front == None
def push(self, e):
s = LinkNode(e)
if self.empty():
self.front = self.rear = s
else:
self.rear.next = s
self.rear = s
def pop(self):
assert not self.empty()
if self.front == self.rear:
e = self.front.data
self.front = self.rear = None
else:
e = self.front.data
self.front = self.front.next
return e
def gethead(self):
assert not self.empty()
return self.front.data
deque (double-ended queue, abbreviation deque) It is extended from the queue :

Double ended queues are the same as queues , The logical relationship of elements is also linear , But the queue can only enter at one end , The other end of the line . The double ended queue can enter and leave the queue at both ends , It has the characteristics of queue and stack , More flexible to use .
It is also very simple to implement a double ended queue from scratch , Omit here . in fact Python Such a data structure is provided in :
from collections import deque
Directly create an empty double ended queue :
q = deque()
q It's empty , It is a dynamically scalable double ended queue .
Create a fixed length double ended queue :
q = deque(maxlen=10)
here q It's empty , But the maximum length is 10. When a new element is added and the double ended queue is full , The oldest element will be automatically removed .
Create a double ended queue from the list :
a = [1, 2, 3, 4, 5]
q = deque(a)
print(q)
# deque([1, 2, 3, 4, 5])
deque There is no method to judge the air , have access to len(q) == 0 To determine whether the double ended queue is empty , The time complexity is zero O ( 1 ) \mathcal{O}(1) O(1).
deque.clear() Clear all elements in the queue deque.append(x) In the line Right Add elements at the end x x x, O ( 1 ) \mathcal{O}(1) O(1)deque.appendleft(x) In the line Left Add elements at the end x x x, O ( 1 ) \mathcal{O}(1) O(1)deque.pop() In the line Right Bring out an element of the team , O ( 1 ) \mathcal{O}(1) O(1)deque.popleft() In the line Left Bring out an element of the team , O ( 1 ) \mathcal{O}(1) O(1)deque.extend(L) In the line Right End add list L L L The elements of deque.extendleft(L) In the line Left End add list L L L The elements of deque.remove(x) Delete the first and x x x Matching elements ( Match from left ), O ( n ) \mathcal{O}(n) O(n)deque.count(x) Statistics x x x The number of , O ( n ) \mathcal{O}(n) O(n)deque.reverse() Reverse queue deque.rotate(n) To the right n n n A place . if n n n It's a negative number , Move left Some examples :
q = deque([1, 2, 3, 4, 5])
q.append(6)
q.appendleft(0)
print(q)
# deque([0, 1, 2, 3, 4, 5, 6])
q.pop()
q.popleft()
print(q)
# deque([1, 2, 3, 4, 5])
q.extend([1, 2, 3])
q.extendleft([7, 8, 9])
print(q)
# deque([9, 8, 7, 1, 2, 3, 4, 5, 1, 2, 3])
q.remove(1)
print(q)
# deque([9, 8, 7, 2, 3, 4, 5, 1, 2, 3])
print(q.count(2))
# 2
q.reverse()
print(q)
# deque([3, 2, 1, 5, 4, 3, 2, 7, 8, 9])
q.rotate(3)
print(q)
# deque([7, 8, 9, 3, 2, 1, 5, 4, 3, 2])
q.clear()
print(q)
# deque([])
The so-called priority queue , Is to specify the priority of the elements in the queue , The higher the priority, the more priority the element will be out of the team . Ordinary queue can be regarded as a special priority queue , The earlier you enter the team, the higher the priority .
Priority queues are usually implemented with heaps , Subsequent articles in this series will introduce , I won't mention it here .
class MyStack:
def __init__(self):
self.q1 = collections.deque()
self.q2 = collections.deque() # Similar to temporary variables temp The role of
def push(self, x: int) -> None:
self.q2.append(x)
while self.q1:
self.q2.append(self.q1.popleft())
self.q1, self.q2 = self.q2, self.q1
def pop(self) -> int:
return self.q1.popleft()
def top(self) -> int:
return self.q1[0]
def empty(self) -> bool:
return not self.q1
class MyStack:
def __init__(self):
self.q = collections.deque()
def push(self, x: int) -> None:
n = len(self.q)
self.q.append(x)
for _ in range(n):
self.q.append(self.q.popleft())
def pop(self) -> int:
return self.q.popleft()
def top(self) -> int:
return self.q[0]
def empty(self) -> bool:
return not self.q
The time complexity and space complexity of the above two methods are the same .
We just need to treat the list as a stack , Then use two stacks to realize .
class MyQueue:
def __init__(self):
self.s1 = []
self.s2 = []
self.front = None
def push(self, x: int) -> None:
if not self.s1: self.front = x
self.s1.append(x)
def pop(self) -> int:
if not self.s2:
while self.s1:
self.s2.append(self.s1.pop())
self.front = None
return self.s2.pop()
def peek(self) -> int:
return self.s2[-1] if self.s2 else self.front
def empty(self) -> bool:
return True if not self.s1 and not self.s2 else False

We can create a dictionary and a queue . The dictionary is used to count the index of each character , For those repeating characters , The dictionary will set its index to − 1 -1 −1.
When traversing a string , Let's first check whether the current character has appeared in the dictionary . If not , Add the character and its corresponding index to the dictionary and queue at the same time ( Join the queue in the form of tuples ). If there has been , We will set the index of this character in the dictionary to − 1 -1 −1, At the same time, constantly check the team head elements , As long as its index in the dictionary is − 1 -1 −1 Just pop up . The final team head element is the first non repeating character we need .
Of course , Team space time , Represents that there are no non repeating characters .
class Solution:
def firstUniqChar(self, s: str) -> int:
hashmap = dict()
q = collections.deque()
for i in range(len(s)):
if s[i] not in hashmap:
hashmap[s[i]] = i
q.append((s[i], i))
else:
hashmap[s[i]] = -1
while q and hashmap[q[0][0]] == -1:
q.popleft()
return -1 if not q else q[0][1]
This method is simple and intuitive .
class Solution:
def firstUniqChar(self, s: str) -> int:
freq = collections.Counter(s)
for i in range(len(s)):
if freq[s[i]] == 1:
return i
return -1