The linked storage structure of a linear table is called Linked list . Each node in the linked list contains not only the information of the element itself , It also contains information about the logical relationship between elements , That is, a node contains the address information of the successor node or the address information of the predecessor node , be called The pointer attribute . In this way, the successor node or precursor node can be easily found through the pointer attribute of a node .
If each node only sets a pointer attribute to its subsequent nodes , Such a linked list is called single ( towards ) Linked list . If each node sets two pointer attributes , It is used to point to its predecessor node and successor node respectively , Such a linked list is called double ( towards ) Linked list . As shown in the figure below :


The corresponding pointer attribute of no predecessor node or successor node is used None Express .
In order to insert and delete nodes in the linked list , Usually, the linked list has a head node , And uniquely identify the linked list through the node pointer .
Will usually p p p The node pointed to is called p p p Node or node p p p, The head node is head The linked list is called head Linked list . No data elements are stored in the header node ( An empty table is a linked list that contains only header nodes ). Generally, the length of the linked list does not count the head node , It only refers to the number of data nodes .
To realize single linked list , We need to create linked list node classes and linked list classes , as follows :
class LinkNode:
def __init__(self, data=None):
self.data = data # Storing data , The default is None, That is, there is no data
self.next = None # The pointer , Used to point to the next node
class LinkList:
def __init__(self):
self.head = LinkNode() # The header node does not contain data , Therefore, no parameters are passed
self.head.next = None # When initializing a linked list , The result is an empty linked list
The method starts with an empty table , Keep reading arrays a a a And generate a new node s s s, then s s s Insert it into the header of the linked list .
def fromlist(self, a):
for i in range(len(a)):
s = LinkNode(a[i])
s.next = self.head.next
self.head.next = s
Time complexity O ( n ) \mathcal{O}(n) O(n), n n n by a a a The number of elements in .
Obvious , The linked list established by head inserting method , The data sequence is the same as a a a The order in is completely opposite .
If you want the data order in the linked list to be consistent with the original array , Tail interpolation can be used . To do this, you need to add a tail pointer t t t, Make it always point to the end of the current list .
def fromlist(self, a):
t = self.head
for i in range(len(a)):
s = LinkNode(a[i])
t.next = s
t = s
t.next = None
Time complexity O ( n ) \mathcal{O}(n) O(n).
In order to realize the correlation operation of linear table in single linked list , We first need to implement a function , That is, the search sequence number is i i i The node of .
def geti(self, i):
p = self.head # Traverse from the beginning of the node
j = -1 # Because the index of the next node pointed by the head node is 0
while j < i and p is not None:
p = p.next
j += 1
return p
Time complexity O ( n ) \mathcal{O}(n) O(n).
def add(self, e):
p = self.head
s = LinkNode(e)
while p.next is not None:
p = p.next
p.next = s
Time complexity O ( n ) \mathcal{O}(n) O(n).
To insert an element, follow these steps :
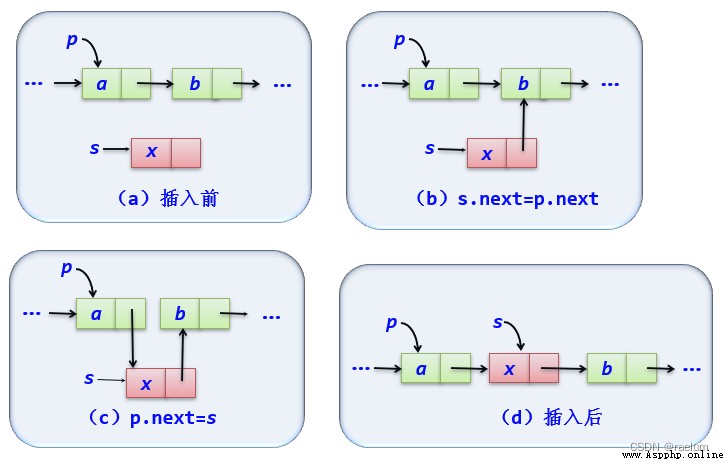
def insert(self, i, e):
assert i >= 0
p = self.geti(i - 1)
assert p is not None
s = LinkNode(e)
s.next = p.next
p.next = s
Time complexity O ( n ) \mathcal{O}(n) O(n).
To delete an element, follow these steps :
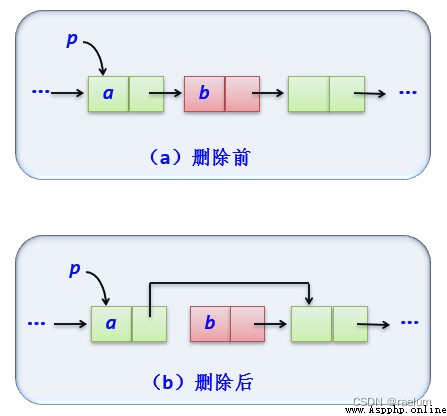
def delete(self, i):
assert i >= 0
p = self.geti(i - 1)
assert p is not None and p.next is not None
p.next = p.next.next
Time complexity O ( n ) \mathcal{O}(n) O(n).
def __getitem__(self, i):
assert i >= 0
p = self.geti(i)
assert p is not None
return p.data
Time complexity O ( n ) \mathcal{O}(n) O(n).
def __setitem__(self, i, x):
assert i >= 0
p = self.geti(i)
assert p is not None
p.data = x
Time complexity O ( n ) \mathcal{O}(n) O(n).
def getno(self, e):
p = self.head.next
k = 0
while p is not None and p.data != e:
p = p.next
k += 1
return -1 if p is None else k # Return... When not found -1
Time complexity O ( n ) \mathcal{O}(n) O(n).
def getsize(self):
p = self.head.next
j = 1
while p.next is not None:
p = p.next
j += 1
return j
Time complexity O ( n ) \mathcal{O}(n) O(n).
Printing a single linked list means printing all the data elements in it .
def display(self):
p = self.head.next
while p.next is not None:
print(p.data, end=' ')
p = p.next
print(p.data)
This printing method can ensure that the characters after the last number are not spaces, but line breaks .
Similar to a single linked list :
class DLinkNode:
def __init__(self, data=None):
self.data = data
self.prior = None
self.next = None
class DLinkList:
def __init__(self):
self.dhead = DLinkNode()
self.dhead.prior = None
self.dhead.next = None
Like a single chain watch , The double linked list is also composed of head nodes head Uniquely identified .
def fromlist(self, a):
for i in range(len(a)):
s = DLinkList(a[i])
# First establish s A two-way relationship with its next node
s.next = self.dhead.next
if self.dhead.next is not None:
self.dhead.next.prior = s
# Re establishment s A two-way relationship with its previous node
self.dhead.next = s
s.prior = self.dhead
def fromlist(self, a):
t = self.dhead
for i in range(len(a)):
s = DLinkList(a[i])
# establish s Two way relationship with the end node of the linked list
t.next = s
s.prior = t
# Move the pointer
t = s
t.next = None
Similar to a single linked list :
def insert(self, i, e):
assert i >= 0
p = self.geti(i - 1)
assert p is not None
s = DLinkNode(e)
s.next = p.next
if p.next is not None:
p.next.prior = s
p.next = s
s.prior = p
Similar to a single linked list :
def delete(self, i):
assert i >= 0
p = self.geti(i)
assert p is not None
p.prior.next = p.next
if p.next is not None:
p.next.prior = p.prior
The pointer attribute of the tail node of the circular single linked list is no longer None, It refers to the head node :
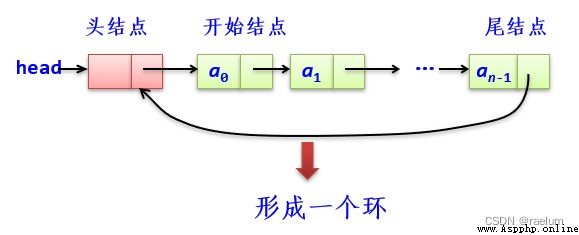
The characteristic of circular single linked list is that you can find other nodes from any node in the table . Compared with single chain table , No need to increase storage space , Only slightly modify the link method , It can make table processing more convenient 、 flexible .
The node type in the circular single linked list is the same as that in the acyclic single linked list , Still LinkNode.
class CLinkList:
def __init__(self):
self.head = LinkNode()
self.head.next = self.head # Because the linked list is empty at the beginning , So the head node refers to the head node
The operations of inserting and deleting nodes in a circular single linked list are the same as those in an acyclic single linked list , So many basic algorithms of the two are similar , The main differences are as follows :
head, In the construction method of circular single linked list, you need to pass head.next = head Statement to set an empty table ;p.next == head instead of p.next == None.Of the tail node of the circular double linked list next Pointer to head node , The first node prior The pointer points to the tail node :
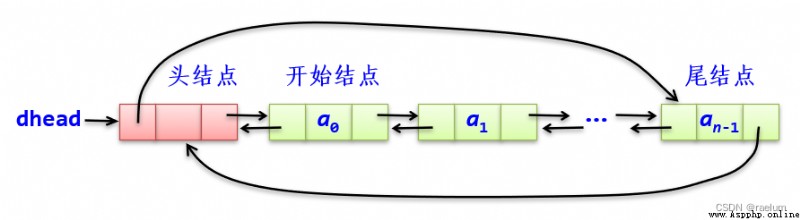
Its characteristic is that the whole linked list forms two rings , From this, you can find other nodes from any node in the table , The most outstanding advantage is through the head node in O ( 1 ) \mathcal{O}(1) O(1) Find the tail node in time .
The node type in the circular double linked list is the same as that in the acyclic double linked list , Still DLinkNode.
class CDLinkList:
def __init__(self):
self.dhead = DLinkNode()
self.dhead.next = self.dhead
self.dhead.prior = self.dhead
For a storage structure , Define its storage density :
save Store The secret degree = The amount of storage occupied by the data itself in the node The storage occupied by the whole node Storage density =\frac{\text{ The amount of storage occupied by the data itself in the node }}{\text{ The storage occupied by the whole node }} save Store The secret degree = The storage occupied by the whole node The amount of storage occupied by the data itself in the node
In a general way , The higher the storage density , The higher the utilization of storage space .
obviously , The storage density of the sequence table is 1, The storage density of linked list is less than 1. Only from the storage density , The storage space utilization of sequential tables is higher .
Besides , The sequence table needs to allocate space in advance , If the space is too small, there will be overflow , If there is too much space, memory will be wasted . The storage space of the linked list is dynamically allocated , As long as there's enough memory , There will be no overflow .
therefore ,
From the perspective of search operation , The sequential table has the characteristics of random storage , Given the sequence number, the time to find the specified element is O ( 1 ) \mathcal{O}(1) O(1); And the linked list does not have the characteristics of random storage , Only sequential access , Given the sequence number, the time to find the specified element is O ( n ) \mathcal{O}(n) O(n).
From the perspective of insert and delete operations , Performing this operation in a sequential table usually requires moving the elements of half the table ; To perform this operation in the linked list, you only need to modify the pointer attribute of the relevant node , You don't have to move nodes .
therefore ,
LeetCode The single linked list node in is defined as :
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
All the following code passed the test .

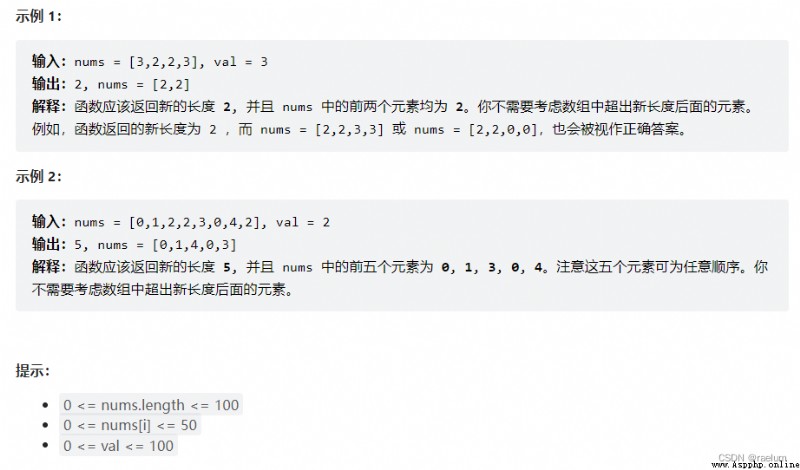
This topic LeetCode Will automatically track
nums, So just return an integer .
We can set two pointers :left and right. Where the right pointer points to the current element to be processed , The left pointer points to the next position to be assigned .
If the element pointed to by the right pointer is equal to val, Then the left pointer does not move , The right pointer moves one bit to the right . otherwise , Copy the element pointed by the right pointer to the position of the left pointer , Then move the left and right pointers to the right one bit at the same time .
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
left = 0
for right in range(len(nums)):
if nums[right] != val:
nums[left] = nums[right]
left += 1
return left
Notice that the algorithm in the worst case , namely nums Does not include val, Both left and right pointers need to traverse the array once , That is, it has been traversed twice in total . Besides , The algorithm will repeatedly assign values to the elements to be preserved ( When left = right when ).
Complexity analysis
Consider initially placing the left and right pointers at both ends of the array .
When the left pointer points to val when , At this point, copy the element pointed to by the right pointer to the left pointer , At the same time, move the right pointer one bit to the left . If the copied element happens to be the same val, Then continue to perform the above operations until the left pointer points to something other than val.
When the left pointer points to something other than val when , Move the left pointer one bit to the right .
When the left and right pointers coincide , The left and right pointers traverse the entire array together .
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
left, right = 0, len(nums) - 1
while left <= right:
if nums[left] == val:
nums[left] = nums[right]
right -= 1
else:
left += 1
return left
Complexity analysis
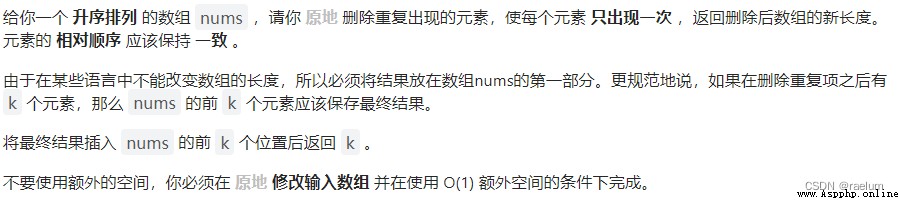
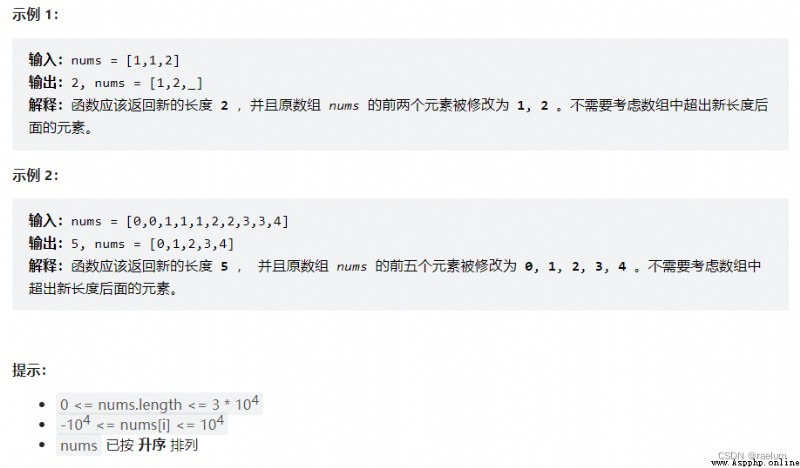
We can know from order , Duplicates must be connected . Besides , Because this question is not given val, So there may be many repetition elements .
say concretely , Set two left and right pointers , Initially, they are all at the left end of the array . When the right pointer points to the same element as the left pointer , The right pointer moves one bit to the right . If different , First move the left pointer to the right by one digit , Then copy the value pointed by the right pointer to the left pointer .
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
left = 0
for right in range(len(nums)):
if nums[left] != nums[right]:
left += 1
nums[left] = nums[right]
return left + 1

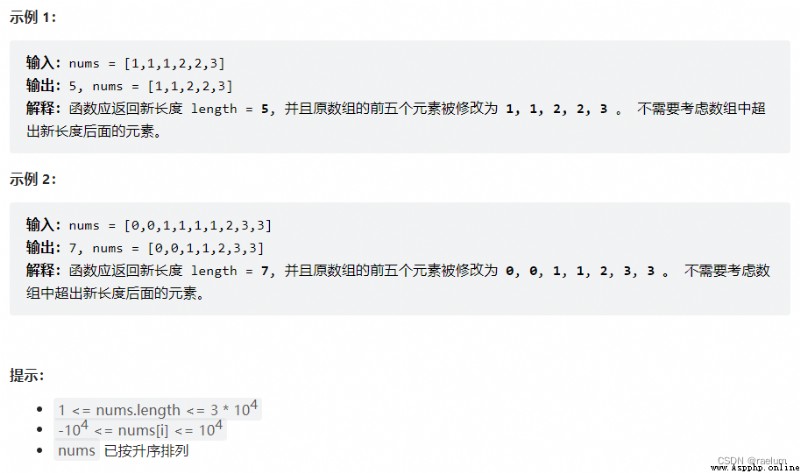
We use the fast and slow pointer solution . Where the slow pointer indicates the length of the processed array , The fast pointer indicates the length of the array that has been checked .
Initially, set the speed pointer to the left end of the array , And the first two numbers of the array should be kept . Therefore, you should initially make the fast and slow pointers move synchronously to the index 2 2 2 Without any modification . Because the same element can appear twice at most , So it's more nums[slow - 2] and nums[fast], When they are the same , Only move the fast pointer to the right one digit ; When they are different , Copy the value pointed by the fast pointer to the left pointer , Then move the left and right pointers one bit to the right .
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
slow = 0
for fast in range(len(nums)):
if slow < 2 or nums[slow - 2] != nums[fast]:
nums[slow] = nums[fast]
slow += 1
return slow


Pendulum rotten solution :
class Solution:
def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
nums = sorted(nums1 + nums2)
n = len(nums)
if n % 2 != 0:
return nums[n // 2]
else:
return (nums[n // 2 - 1] + nums[n // 2]) / 2
Because of the call sorted function , So time complexity is O ( ( m + n ) log ( m + n ) ) \mathcal{O}((m+n)\log(m+n)) O((m+n)log(m+n)). So although the above code can run successfully , But it does not meet the requirements of the topic .
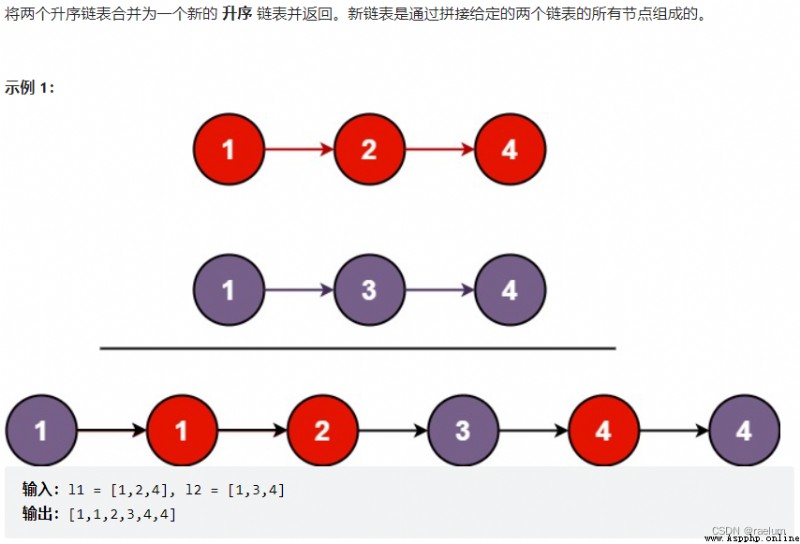

First set a sentinel node sentinel, This makes it easier to return to the merged linked list at the end . We set three pointers l1、l2 and prev,l1 and l2 To traverse separately list1 and list2. At the beginning prev Point to the sentinel node .
When l1 Less than l2 when , We will l1 The node pointed to is connected to prev after , And then prev and l1 Move back one bit . otherwise , We will l2 The node pointed to is connected to prev after , And then prev and l2 Move back one bit .
When the loop ends ,l1 and l2 At most one is not empty , Because the two input lists are ordered , So we just need to simply connect the non empty linked list to the merged linked list , And return to the merge list .
class Solution:
def mergeTwoLists(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:
sentinel = ListNode(-1)
prev = sentinel
while l1 and l2:
if l1.val < l2.val:
prev.next = l1
l1 = l1.next
else:
prev.next = l2
l2 = l2.next
prev = prev.next
prev.next = l2 if l1 is None else l1
return sentinel.next
Time complexity : O ( m + n ) \mathcal{O}(m+n) O(m+n), Spatial complexity : O ( 1 ) \mathcal{O}(1) O(1).
class Solution:
def mergeTwoLists(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:
# The boundary conditions
if l1 is None:
return l2
if l2 is None:
return l1
# Recursive body
if l1.val < l2.val:
l1.next = self.mergeTwoLists(l1.next, l2)
return l1
else:
l2.next = self.mergeTwoLists(l1, l2.next)
return l2
Time complexity : O ( m + n ) \mathcal{O}(m+n) O(m+n), Spatial complexity : O ( m + n ) \mathcal{O}(m+n) O(m+n).
Recursively call
mergeTwoListsFunction needs to consume stack space , The size of the stack space depends on the depth of the recursive call . End recursive callmergeTwoListsThe function can call at most n + m n+m n+m Time , So the space complexity is zero O ( n + m ) \mathcal{O}(n+m) O(n+m).

class Solution:
def deleteDuplicates(self, head: ListNode) -> ListNode:
if not head:
return head
cur = head
while cur.next:
if cur.val == cur.next.val:
cur.next = cur.next.next
else:
cur = cur.next
return head
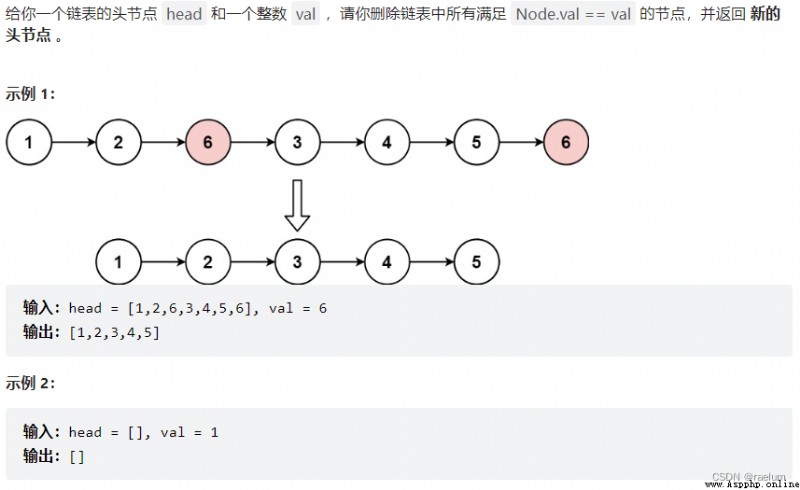

Because the head node may change , So we still use the sentinel node method . Besides , Set a pointer cur Used to traverse the entire list .
class Solution:
def removeElements(self, head: ListNode, val: int) -> ListNode:
if not head: return head
sentinel = ListNode(-1)
sentinel.next = head
cur = sentinel
while cur.next:
if cur.next.val == val:
cur.next = cur.next.next
else:
cur = cur.next
return sentinel.next
This problem can still be solved recursively .
class Solution:
def removeElements(self, head: ListNode, val: int) -> ListNode:
if not head: return head
head.next = self.removeElements(head.next, val)
# If head It needs to be deleted , Then return to head Next node of , Otherwise return to head In itself
return head.next if head.val == val else head
First of all, the easiest way to think of is to traverse twice . The first traverse calculates the total length of the linked list , The second traversal determines the node to be deleted . This method is too simple and crude, so I won't introduce it here .
For this question , We can set a speed pointer , Find a way to get the fast pointer to the end of the linked list , The slow pointer is just the penultimate n + 1 n+1 n+1 Nodes .
class Solution:
def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
sentinel = ListNode(-1, head)
slow, fast = sentinel, head
for _ in range(n):
fast = fast.next
while fast:
fast = fast.next
slow = slow.next
slow.next = slow.next.next
return sentinel.next
The roughest way is to store the values of the linked list in a list in turn nums in , And then through nums==nums[::-1] To judge whether the given list is a palindrome list .
Another idea is to press the first half of the linked list into the stack in turn , Then pop up the elements in the stack in turn and compare them with the latter half of the linked list . This method needs to consider the parity of the length of the linked list .
The space complexity of the above two methods is O ( n ) \mathcal{O}(n) O(n), Here is a O ( 1 ) \mathcal{O}(1) O(1) Solutions for —— Fast and slow pointer method .
The whole process is divided into the following steps :
class Solution:
def isPalindrome(self, head: ListNode) -> bool:
if not head: return True
first_half_end = self.get_middle_position(head)
second_half_start = self.reverse_list(first_half_end.next)
flag = True
left, right = head, second_half_start
while flag and right:
if left.val != right.val:
flag = False
left = left.next
right = right.next
return flag
def get_middle_position(self, head):
slow, fast = head, head
while fast.next and fast.next.next:
slow = slow.next
fast = fast.next.next
return slow
def reverse_list(self, head):
prev, cur = None, head
while cur:
next_node = cur.next
cur.next = prev
prev = cur
cur = next_node
return prev
Strictly speaking , We should also restore the linked list after judgment .


You can first form a circular linked list , Then cut the designated position .
class Solution:
def rotateRight(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:
if not head: return head
# Form a circular linked list and calculate the length of the linked list
p = head
length = 1
while p.next:
p = p.next
length += 1
p.next = head
# break link
pos = length - k % length
p = head
k = 1
while k < pos:
p = p.next
k += 1
next_node = p.next
p.next = None
return next_node
class LinkNode:
def __init__(self, data=None):
self.data = data
self.next = None
class LinkList:
def __init__(self):
self.head = LinkNode()
self.head.next = None
def fromlist(self, a):
t = self.head
for i in range(len(a)):
s = LinkNode(a[i])
t.next = s
t = s
t.next = None
def geti(self, i):
p = self.head
j = -1
while j < i and p is not None:
p = p.next
j += 1
return p
def add(self, e):
p = self.head
s = LinkNode(e)
while p.next is not None:
p = p.next
p.next = s
def insert(self, i, e):
assert i >= 0
p = self.geti(i - 1)
assert p is not None
s = LinkNode(e)
s.next = p.next
p.next = s
def delete(self, i):
assert i >= 0
p = self.geti(i - 1)
assert p is not None and p.next is not None
p.next = p.next.next
def __getitem__(self, i):
assert i >= 0
p = self.geti(i)
assert p is not None
return p.data
def __setitem__(self, i, x):
assert i >= 0
p = self.geti(i)
assert p is not None
p.data = x
def getno(self, e):
p = self.head.next
k = 0
while p is not None and p.data != e:
p = p.next
k += 1
return -1 if p is None else k
def getsize(self):
p = self.head.next
j = 1
while p.next is not None:
p = p.next
j += 1
return j
def display(self):
p = self.head.next
while p.next is not None:
print(p.data, end=' ')
p = p.next
print(p.data)
class DLinkNode:
def __init__(self, data=None):
self.data = data
self.prior = None
self.next = None
class DLinkList:
def __init__(self):
self.dhead = DLinkNode()
self.dhead.prior = None
self.dhead.next = None
def fromlist(self, a):
t = self.dhead
for i in range(len(a)):
s = DLinkList(a[i])
# establish s Two way relationship with the end node of the linked list
t.next = s
s.prior = t
# Move the pointer
t = s
t.next = None
def geti(self, i):
p = self.dhead
j = -1
while j < i and p is not None:
p = p.next
j += 1
return p
def insert(self, i, e):
assert i >= 0
p = self.geti(i - 1)
assert p is not None
s = DLinkNode(e)
s.next = p.next
if p.next is not None:
p.next.prior = s
p.next = s
s.prior = p
def delete(self, i):
assert i >= 0
p = self.geti(i)
assert p is not None
p.prior.next = p.next
if p.next is not None:
p.next.prior = p.prior