隊列是一種操作受限的線性表，其限制為僅允許在表的一端插入，而在表的另一端進行刪除。把進行插入的一端稱為隊尾（rear），把進行刪除的一端稱作隊頭或隊首（front）。向隊列中插入元素稱為進隊或入隊，從隊列中刪除元素稱為出隊或離隊。
隊列的一個顯著特點是：FIFO（First In First Out）。
隊列需要實現的方法和棧一樣：empty()、push(e)、pop() 和 gethead()。
采用順序存儲結構的隊列稱為順序隊。我們用列表 data 來存放隊列中的元素，另外設置兩個指針，隊頭指針為 front，隊尾指針為 rear。
為簡單起見，這裡使用固定容量的列表：
front 指向隊頭元素的前一個位置，而 rear 正好指向隊尾元素。
順序隊分為非循環隊列和循環隊列兩種結構，下面先討論非循環隊列，並通過說明該類型隊列的缺點引出循環隊列。
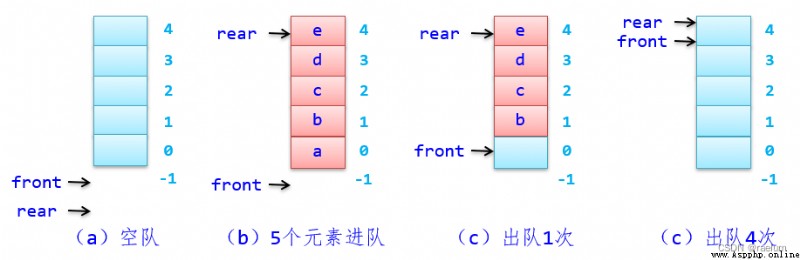
初始時置 front 和 read 均為 -1，非循環隊列的四要素如下：
front == rear;rear = MaxSize - 1；rear 增加 1，並將 e e e 放在該位置（進隊的元素總是在尾部插入的）；front 增加 1，取出該位置的元素（出隊的元素總是在隊頭出來的）。非循環隊列的架構如下：
class SqQueue:
def __init__(self):
self.__MaxSize = 100
self.data = [None] * self.__MaxSize
self.front = self.rear = -1
完整實現：
class SqQueue:
def __init__(self):
self.__MaxSize = 100
self.data = [None] * self.__MaxSize
self.front = self.rear = -1
def empty(self):
return self.front == self.rear
def push(self, e):
assert self.rear != self.__MaxSize - 1
self.rear += 1
self.data[self.rear] = e
def pop(self):
assert not self.empty()
self.front += 1
return self.data[self.front]
def gethead(self):
assert not self.empty()
return self.data[self.front + 1]
上述操作的時間復雜度均為 O ( 1 ) \mathcal{O}(1) O(1)。
在非循環隊列中，元素進隊時隊尾指針 rear += 1，元素出隊時有 front += 1。當隊滿，即 rear = MaxSize - 1 成立時，此時即使仍出隊若干元素，改變的只是 front 的位置，而 rear 不變，即隊滿條件仍然成立。這種隊列中有空位置但仍然滿足隊滿條件的上溢出稱為假溢出。也就是說，非循環隊列存在假溢出現象。
為了克服假溢出，充分利用數組的存儲空間，我們可以把 data 數組的前端和後端連接起來，形成一個循環數組，即把存儲隊列元素的表從邏輯上看成一個環，稱為循環隊列。
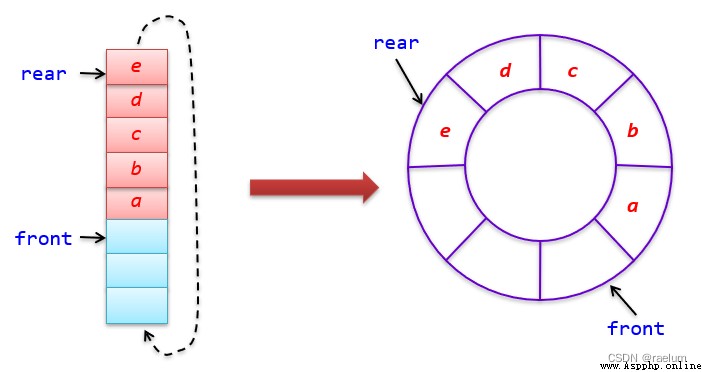
循環隊列首尾相連，當隊尾指針 rear = MaxSize - 1 時，再前進一個位置就到達 0，這可以利用求余運算進行實現：
循環隊列的隊頭指針和隊尾指針初始時均指向 0（即真實位置，不像非循環隊列的隊頭指針和隊尾指針初始時均指向虛擬位置 -1）。有元素進隊時，rear += 1，有元素出隊時，front += 1。
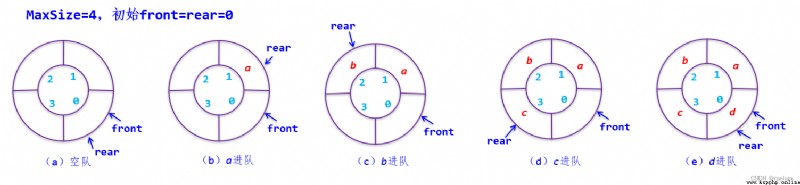
從上圖還能發現一個細節：隊空和隊滿時均有 rear == front，那我們該如何判斷隊空呢？事實上我們需要添加一個約束，具體如下。
循環隊列和非循環隊列都需要通過 front 和 rear 來標識隊列狀態。我們知道，一個長度為 m m m 的隊列有以下 m + 1 m+1 m+1 種狀態：
若采取 |front - rear| 的方式來標識循環隊列的狀態，因為 front 和 rear 的取值范圍為 0 ∼ m − 1 0\sim m-1 0∼m−1，從而 |front - rear| 只有 m m m 種取值。注意到 m < m + 1 m<m+1 m<m+1，所以如果采用 |front - rear| 來區分隊列狀態的話，必定有兩種狀態不能區分。所以如果我們限制長度為 m m m 的隊列最多含有 m − 1 m-1 m−1 個元素的話，就可以使用 |front - rear| 去區分所有的隊列狀態了。
為什麼是有兩種狀態不能區分而不是有一種？我們可以考慮最簡單的情形，假設隊列長度為 1 1 1，因此只有兩種狀態：隊空，隊中只有一個元素（即隊滿）。此時
|front - rear|只有一種取值： 0 0 0，我們無法通過該值來判斷隊列的具體狀態。
在規定了循環隊列最多含有 m − 1 m-1 m−1 個元素後，我們就可以使用 rear == front 來判定隊空了。當隊滿時（即隊列中含有 m − 1 m-1 m−1 個元素），一定有 (rear + 1) % MaxSize == front。於是我們得到循環隊列的四要素：
rear == front；(rear + 1) % MaxSize == front；rear = (rear + 1) % MaxSize，再將 e e e 放在該位置；front = (front + 1) % MaxSize，取出該位置的元素。完整實現如下：
class CSqQueue:
def __init__(self):
self.__MaxSize = 100
self.data = [None] * self.__MaxSize
self.front = self.rear = 0
def empty(self):
return self.front == self.rear
def push(self, e):
assert (self.rear + 1) % self.__MaxSize != self.front
self.rear = (self.rear + 1) % self.__MaxSize
self.data[self.rear] = e
def pop(self):
assert not self.empty()
self.front = (self.front + 1) % self.__MaxSize
return self.data[self.front]
def gethead(self):
assert not self.empty()
return self.data[(self.front + 1) % self.__MaxSize]
上述操作的時間復雜度均為 O ( 1 ) \mathcal{O}(1) O(1)。
隊列的鏈式存儲結構簡稱鏈隊。它是通過由結點構成的單鏈表進行實現的。此時只允許在單鏈表的表頭進行刪除操作，在單鏈表的表尾進行插入操作。
需要注意的是，這裡的單鏈表是不帶頭結點的，並且需要兩個指針來標識該單鏈表。其中 front 指向隊首結點，rear 指向隊尾結點。
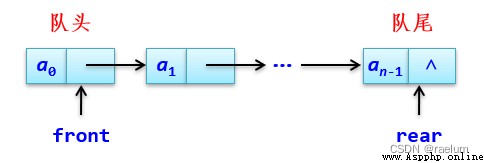
基本架構如下：
class LinkNode:
def __init__(self, data=None, next=None):
self.data = data
self.next = next
class LinkQueue:
def __init__(self):
self.front = None
self.rear = None
鏈隊的四要素如下：
front == rear == None，不妨僅以 front == None 作為隊空條件；rear 指向它；data 值並將其從鏈隊中刪除。class LinkQueue:
def __init__(self):
self.front = None
self.rear = None
def empty(self):
return self.front == None
def push(self, e):
s = LinkNode(e)
if self.empty():
self.front = self.rear = s
else:
self.rear.next = s
self.rear = s
def pop(self):
assert not self.empty()
if self.front == self.rear:
e = self.front.data
self.front = self.rear = None
else:
e = self.front.data
self.front = self.front.next
return e
def gethead(self):
assert not self.empty()
return self.front.data
雙端隊列（double-ended queue，簡稱deque）是在隊列的基礎上擴展而來的：
雙端隊列與隊列一樣，元素的邏輯關系也是線性關系，但隊列只能在一端進隊，另一端出隊。而雙端隊列可以在兩端進行進隊和出隊的操作，具有隊列和棧的特性，使用起來更加靈活。
從零開始實現一個雙端隊列也非常簡單，這裡略去。事實上Python中提供了這樣的數據結構：
from collections import deque
直接創建一個空的雙端隊列：
q = deque()
q 為空，它是一個可動態擴展的雙端隊列。
創建一個固定長度的雙端隊列：
q = deque(maxlen=10)
此時 q 為空，但最大長度為 10。當有新元素加入且雙端隊列已滿時，會自動移除最老的元素。
從列表中創建一個雙端隊列：
a = [1, 2, 3, 4, 5]
q = deque(a)
print(q)
# deque([1, 2, 3, 4, 5])
deque 沒有提供判空方法，可以使用 len(q) == 0 來判斷雙端隊列是否為空，其時間復雜度是 O ( 1 ) \mathcal{O}(1) O(1)。
deque.clear()清除隊列中的所有元素deque.append(x)在隊列右端添加元素 x x x， O ( 1 ) \mathcal{O}(1) O(1)deque.appendleft(x)在隊列左端添加元素 x x x， O ( 1 ) \mathcal{O}(1) O(1)deque.pop()在隊列右端出隊一個元素， O ( 1 ) \mathcal{O}(1) O(1)deque.popleft()在隊列左端出隊一個元素， O ( 1 ) \mathcal{O}(1) O(1)deque.extend(L)在隊列右端添加列表 L L L 的元素deque.extendleft(L)在隊列左端添加列表 L L L 的元素deque.remove(x)刪除首個與 x x x 匹配的元素（從左開始匹配）， O ( n ) \mathcal{O}(n) O(n)deque.count(x)統計 x x x 的個數， O ( n ) \mathcal{O}(n) O(n)deque.reverse()反轉隊列deque.rotate(n)向右移動 n n n 個位置。若 n n n 是負數，則向左移一些例子：
q = deque([1, 2, 3, 4, 5])
q.append(6)
q.appendleft(0)
print(q)
# deque([0, 1, 2, 3, 4, 5, 6])
q.pop()
q.popleft()
print(q)
# deque([1, 2, 3, 4, 5])
q.extend([1, 2, 3])
q.extendleft([7, 8, 9])
print(q)
# deque([9, 8, 7, 1, 2, 3, 4, 5, 1, 2, 3])
q.remove(1)
print(q)
# deque([9, 8, 7, 2, 3, 4, 5, 1, 2, 3])
print(q.count(2))
# 2
q.reverse()
print(q)
# deque([3, 2, 1, 5, 4, 3, 2, 7, 8, 9])
q.rotate(3)
print(q)
# deque([7, 8, 9, 3, 2, 1, 5, 4, 3, 2])
q.clear()
print(q)
# deque([])
所謂優先級隊列，就是指定隊列中元素的優先級，優先級越大的元素越優先出隊。普通隊列可以看成一種特殊的優先級隊列，進隊越早優先級越高。
優先級隊列通常用堆來實現，本系列的後續文章將會介紹，這裡不再提及。
class MyStack:
def __init__(self):
self.q1 = collections.deque()
self.q2 = collections.deque() # 類似於臨時變量temp的作用
def push(self, x: int) -> None:
self.q2.append(x)
while self.q1:
self.q2.append(self.q1.popleft())
self.q1, self.q2 = self.q2, self.q1
def pop(self) -> int:
return self.q1.popleft()
def top(self) -> int:
return self.q1[0]
def empty(self) -> bool:
return not self.q1
class MyStack:
def __init__(self):
self.q = collections.deque()
def push(self, x: int) -> None:
n = len(self.q)
self.q.append(x)
for _ in range(n):
self.q.append(self.q.popleft())
def pop(self) -> int:
return self.q.popleft()
def top(self) -> int:
return self.q[0]
def empty(self) -> bool:
return not self.q
上述兩種方法的時間復雜度和空間復雜度均相同。
我們只需把列表當作棧，然後用兩個棧來實現即可。
class MyQueue:
def __init__(self):
self.s1 = []
self.s2 = []
self.front = None
def push(self, x: int) -> None:
if not self.s1: self.front = x
self.s1.append(x)
def pop(self) -> int:
if not self.s2:
while self.s1:
self.s2.append(self.s1.pop())
self.front = None
return self.s2.pop()
def peek(self) -> int:
return self.s2[-1] if self.s2 else self.front
def empty(self) -> bool:
return True if not self.s1 and not self.s2 else False
我們可以創建一個字典和一個隊列。字典用來統計每個字符的索引，對於那些重復字符，字典會將其索引置為 − 1 -1 −1。
遍歷字符串時，我們先檢查當前字符是否已經出現在字典中。如果沒有出現，就將該字符和其對應的索引同時添加到字典和隊列中（以元組的形式加入隊列）。如果已經出現過，我們就將字典中該字符的索引置為 − 1 -1 −1，同時不斷檢查隊頭元素，只要它在字典中的索引為 − 1 -1 −1 就彈出。最後得到的隊頭元素就是我們需要的第一個不重復的字符。
當然，隊空時，代表沒有不重復的字符。
class Solution:
def firstUniqChar(self, s: str) -> int:
hashmap = dict()
q = collections.deque()
for i in range(len(s)):
if s[i] not in hashmap:
hashmap[s[i]] = i
q.append((s[i], i))
else:
hashmap[s[i]] = -1
while q and hashmap[q[0][0]] == -1:
q.popleft()
return -1 if not q else q[0][1]
該方法簡單直觀。
class Solution:
def firstUniqChar(self, s: str) -> int:
freq = collections.Counter(s)
for i in range(len(s)):
if freq[s[i]] == 1:
return i
return -1
[advanced Python Script] 2.2. Build an SSH botnet (Part 2): use the weak private key in SSH
Catalog One 、 brief introduct
The python program visualization I used gooey to do is packaged with pyinstaller. After the program runs, enter parameters, and click start to display a black box;
I am here pyinstaller Packed w
