Stack is a method that can only be used in At the same end Insert / Delete the The linear table . Insertion is allowed in the table / One end of the delete operation is called To the top of the stack . The current position of the top of the stack is dynamic , You can use a position indicator called the stack top pointer to indicate . The other end of the table is called At the bottom of the stack . When there are no elements in the stack, it is called Empty stack . The insertion operation of stack is usually called Into the stack or Push , The deletion of the stack is usually called Out of the stack or Backstack .
A major feature of stack is LIFO, namely Last In First Out.
The definition of abstract data type stack is as follows :
Data objects : D = { a i ∣ 0 ≤ i ≤ n − 1 , n ≥ 0 } Data relation : R = { r } r = { < a i , a i + 1 > ∣ a i , a i + 1 ∈ D , i = 0 , ⋯ , n − 2 } Basic operation : empty() : sentence break Stack yes no by empty push(e) : take e Pressure Enter into Stack in pop() : take Out Stack The top element plain gettop() : return return Stack The top element plain \begin{aligned} &\text{ Data objects :} D=\{a_i|0\leq i\leq n-1,n\geq0\} \\ &\text{ Data relation :} \\ &\quad R = \{r\} \\ &\quad r=\{<a_i,a_{i+1}>|a_i,a_{i+1}\in D,i=0,\cdots, n-2\} \\ &\text{ Basic operation :} \\ &\quad \text{empty()}: Judge whether the stack is empty \\ &\quad \text{push(e)}: take e Pressure into the stack \\ &\quad \text{pop()}: Take out the top element of the stack \\ &\quad \text{gettop()}: Back to top of stack element \\ \end{aligned} Data objects :D={ ai∣0≤i≤n−1,n≥0} Data relation :R={ r}r={ <ai,ai+1>∣ai,ai+1∈D,i=0,⋯,n−2} Basic operation :empty(): sentence break Stack yes no by empty push(e): take e Pressure Enter into Stack in pop(): take Out Stack The top element plain gettop(): return return Stack The top element plain
Because the logical relationship of the elements in the stack is the same as that of the linear table , Therefore, we can learn from the two storage structures of linear tables to store stacks .
When using sequential storage structure to store , Use list data To store the elements in the stack , be called Order of the stack . because Python The list provides the function of dynamic expansion at one end , For this reason will data[0] As the bottom of the stack , take data[-1] As the top of the stack , among len(data) Represents the number of elements in the stack .
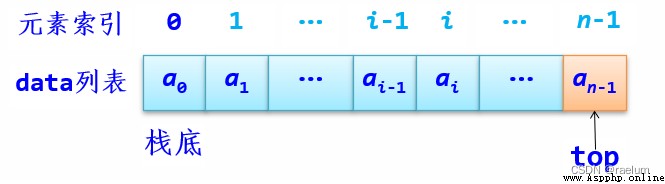
Next, we directly and completely implement the basic functions of the sequence stack :
class SqStack:
def __init__(self):
self.data = []
def empty(self):
return len(self.data) == 0
def push(self, e):
self.data.append(e)
def pop(self):
assert not self.empty()
return self.data.pop()
def gettop(self):
assert not self.empty()
return self.data[-1]
You can see from the above , The time complexity of various basic operations of the stack is O ( 1 ) \mathcal{O}(1) O(1).
Suppose that the expression entered by the user contains parentheses 、 Square brackets and curly braces , And only these brackets . Design an algorithm to determine whether the parentheses in the expression are paired .
We can use sequence stack to solve this problem :
def is_match(string):
stack = SqStack()
for e in string:
if e == '(' or e == '[' or e == '{':
stack.push(e)
else:
if e == ')':
if stack.empty() or stack.gettop() != '(':
return False
stack.pop()
if e == ']':
if stack.empty() or stack.gettop() != '[':
return False
stack.pop()
if e == '}':
if stack.empty() or stack.gettop() != '{':
return False
stack.pop()
return stack.empty()
string_1 = '([)]'
string_2 = '([])'
print(is_match(string_1))
# False
print(is_match(string_2))
# True
Design a minimum stack . That is, based on the original stack structure , Add one getmin() Method , Used in O ( 1 ) \mathcal{O}(1) O(1) Return the smallest element in the stack within the time of .
We can add one to the original mindata list , among data The list represents the main stack ,mindata The list represents the auxiliary stack , Used to store the current minimum element ( notes :mindata There may be multiple elements in ).
class SqStack:
def __init__(self):
self.data = []
self.__mindata = []
""" min The basic operation of stack """
def __minempty(self):
return len(self.__mindata) == 0
def __minpush(self, e):
self.__mindata.append(e)
def __minpop(self):
assert not self.__minempty()
return self.__mindata.pop()
def __mingettop(self):
assert not self.__minempty()
return self.__mindata[-1]
""" Basic operation of main stack """
def empty(self):
return len(self.data) == 0
def push(self, e):
if self.empty() or e <= self.getmin():
self.__mindata.append(e)
self.data.append(e)
def pop(self):
assert not self.empty()
x = self.data.pop()
if x == self.__mingettop():
self.__minpop()
return x
def gettop(self):
assert not self.empty()
return self.data[-1]
def getmin(self):
assert not self.empty()
return self.__mindata[-1]
The stack with chain storage structure is called chain stack , Here we use single linked list to realize .
The advantage of chain stack is that it doesn't need to consider stack overflow .

As shown in the figure , The first node is the top node of the stack , The tail node is the bottom node . The four elements of the chain stack are as follows :
head.next == None;The type of each node in the chain stack is the same as that of the ordinary single chain list :
class LinkNode:
def __init__(self, data=None, next=None):
self.data = data
self.next = next
The design of the chain stack class is as follows :
class LinkStack:
def __init__(self):
self.head = LinkNode()
self.head.next = None
Next, we implement the basic operation of the stack in the chain stack :
class LinkStack:
def __init__(self):
self.head = LinkNode()
self.head.next = None
def empty(self):
return self.head.next == None
def push(self, e):
s = LinkNode(e)
s.next = self.head.next
self.head.next = s
def pop(self):
assert not self.empty()
p = self.head.next
self.head.next = p.next
return p.data
def gettop(self):
assert not self.empty()
return self.head.next.data
The same stack sequence can produce different stack sequences . for example , Set the stack sequence as ( 1 , 2 , 3 , 4 , 5 ) (1,2,3,4,5) (1,2,3,4,5), We can let 1 , 2 , 3 1,2,3 1,2,3 Push 、 Out of the stack , let 4 , 5 4,5 4,5 Push 、 Out of the stack , The stack sequence thus obtained is ( 3 , 2 , 1 , 5 , 4 ) (3,2,1,5,4) (3,2,1,5,4). We can also let 1 , 2 1,2 1,2 Push 、 Out of the stack , let 3 , 4 , 5 3,4,5 3,4,5 Push 、 Out of the stack , The stack sequence thus obtained is ( 2 , 1 , 5 , 4 , 3 ) (2,1,5,4,3) (2,1,5,4,3).
Given the stack sequence a, Design an algorithm to judge b Whether it is a Legal stack sequence of ( among a and b Are all 1 ∼ n 1\sim n 1∼n An arrangement of ).
We just need to simulate the process :
def is_valid(a, b):
stack = SqStack()
j = 0
for i in range(len(a)):
stack.push(a[i])
while not stack.empty() and stack.gettop() == b[j]:
stack.pop()
j += 1
return stack.empty()
print(is_valid([1, 2, 3, 4], [1, 3, 2, 4]))
# True
print(is_valid([1, 2, 3, 4], [4, 3, 1, 2]))
# False



The problem is very simple , There is no need for too much explanation .
But here's the thing , For the sake of simplicity , We use lists directly to simulate stacks , No longer write a class alone .
class Solution:
def simplifyPath(self, path: str) -> str:
stack = list()
for s in path.split('/'):
if s:
if s != '.' and s != '..':
stack.append(s)
if s == '..' and stack:
stack.pop()
return '/' + '/'.join(stack)


class Solution(object):
def asteroidCollision(self, asteroids):
stack = list()
for new in asteroids:
while stack and new < 0 < stack[-1]:
if stack[-1] < -new:
stack.pop()
continue
elif stack[-1] == -new:
stack.pop()
break
else:
stack.append(new)
return stack
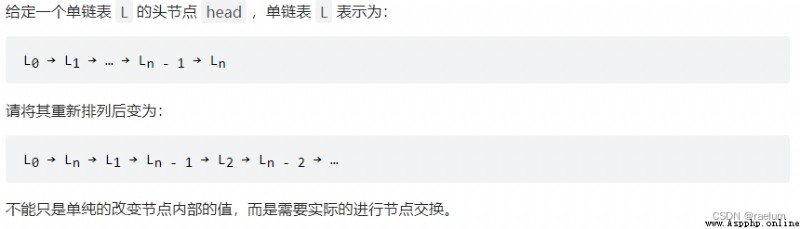
The specific idea is , First, find the intermediate node , Then cut off the first half and the second half of the list , Then reverse the linked list in the second half , Finally, merge the two linked lists .
class Solution:
def reorderList(self, head: ListNode) -> None:
if not head:
return
mid = self.middleNode(head)
l1 = head
l2 = mid.next
mid.next = None
l2 = self.reverseList(l2)
self.mergeList(l1, l2)
def middleNode(self, head: ListNode) -> ListNode:
slow = fast = head
while fast.next and fast.next.next:
slow = slow.next
fast = fast.next.next
return slow
def reverseList(self, head: ListNode) -> ListNode:
prev = None
curr = head
while curr:
nextTemp = curr.next
curr.next = prev
prev = curr
curr = nextTemp
return prev
def mergeList(self, l1: ListNode, l2: ListNode):
while l1 and l2:
l1_tmp = l1.next
l2_tmp = l2.next
l1.next = l2
l1 = l1_tmp
l2.next = l1
l2 = l2_tmp