一般的曲率計算方法,如玄長比例法、三次B樣條表達、線性多邊形逼近和局部對稱等方法。今天主要介紹 彎曲值算法(Bending value) 算法。其表達式為:
b i k = m a x ( ∣ ( x i − k − x i ) + ( x i + k − x i ) ) ∣ , ∣ ( y i − k − y i ) + ( y i + k − y i ) ∣ ) b_{ik}=max(|(x_{i-k}-x_{i})+(x_{i+k}-x_{i}))|,|(y_{i-k}-y_{i})+(y_{i+k}-y_{i})|) bik=max(∣(xi−k−xi)+(xi+k−xi))∣,∣(yi−k−yi)+(yi+k−yi)∣)
計算Bending Value的示意圖如下: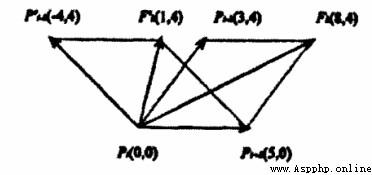

參考鏈接:
手寫體漢字的書寫質量評價
計算線段上每一點的Bending Value,記作 B v ( i ) Bv(i) Bv(i),這裡需要初始化阈值delta=1.1和搜索范圍k=1
當 B v ( i ) > d e l t a Bv(i)>delta Bv(i)>delta,且對於所有 i − k < = j < = i + k i-k<=j<=i+k i−k<=j<=i+k,均有 B v ( i ) > = B v ( j ) Bv(i)>=Bv(j) Bv(i)>=Bv(j),則該點符合局部曲率最大的性質,作為候選拐點。
篩選條件一:判斷候選拐點相鄰三點 p i − 1 p_{i-1} pi−1、 p i p_{i} pi、 p i + 1 p_{i+1} pi+1是否位於同一條直線上,如果在則排除該點
篩選條件二:計算自適應彎曲值(Bending Value)。算法流程如下:
計算候選點的搜索范圍k從1開始增加,用 b i k b_{ik} bik表示當前Bending Value。如果 b i k > = b i k + 1 b_{ik}>=b_{ik+1} bik>=bik+1,k增加1,否則停止增加。求得連續的Bending Value值後,需要再進行求平均值,作為最終該點的彎曲值,計算公式如下:
b v i = 1 k i ∑ j = 1 k i b i j b_{v_{i}}=\frac{1}{k_{i}}\sum^{k_{i}}_{j=1}b_{ij} bvi=ki1j=1∑kibij
根據計算的自適應拐點,還需要滿足以下條件:
條件一表示Bending Value值應大於阈值,條件二、三、四表示拐點必須為局部最大值
當獲取曲線的點整後點與點之間可能存在較大的間隔,需要我們對這些點進行一個采樣來增加其連續性。一般采樣方法有DDA、一次貝塞爾曲線擬合、二次貝塞爾曲線擬合或三次貝塞爾曲線離合。其中DDA和一次貝塞爾曲線擬合類似。都是通過兩點之間直線的斜率來進行一個采樣,當然使用更高階的方法,采樣曲線也更加平滑。

如上圖所示,對於平面上的兩個點 P0 和 P1,假設另一點 B 勻速地從 P0 點運動到 P1 點,則有 B 點在 t 時刻的坐標公式:

將 B 點在各個時刻的坐標依次連接起來所形成的線,就是所謂的貝塞爾曲線。此公式表示的是一次貝塞爾曲線,也稱為線性貝塞爾曲線。
python實現如下:
def getFirstBezierPointByT(start,end,t):
''' 根據一次貝爾曲線的的計算公式計算各個時刻的坐標值 :param start: :param end: :param t: :return: '''
x=(1-t)*start[0]+t*end[0]
y=(1-t)*start[1]+t*end[1]
return [x,y]
def calculateFirstBezierPoints(start,end):
''' 計算兩點之間的塞爾曲線點集 :param start: :param handle: :param end: :return: '''
bx=start[0]
by=start[1]
ex=end[0]
ey=end[1]
beDis=math.sqrt(math.pow((bx-ex),2)+math.pow((by-ey),2))
count=int(beDis//1)
if count<2:
return [start]
step = 1.0 / count
points=[]
t = 0.0
for i in range(count):
points.append(getFirstBezierPointByT(start, end, t))
t += step
return points
def firstBezierCurveFitting(pts):
''' 一次貝塞爾曲線擬合 :param pts: :return: '''
new_pts = []
for pt in pts:
new_pt = []
for i in range(0, (len(pt) - 1)):
pp=calculateFirstBezierPoints(pt[i], pt[i + 1])
new_pt += pp
new_pt.append(pt[len(pt)-1])
new_pts.append(new_pt)
return new_pts

同樣地,對於平面上的三個點 P0、P1 和 P2 ,假設 P0P1 之間有個點 B1 勻速地從 P0 運動到 P1 ,P1P2 之間有個點 B2 勻速地從 P1 運動到 P2,則有:


假設另一點 B 勻速地從 B1 運動到 B2,則有 B 點的坐標公式:

將 B1 和 B2 的坐標公式代入上面的表達式,整理後得到 B 點的坐標公式:

B 點在各個時刻的坐標所連成的曲線即為二次貝塞爾曲線,其中 P0 和 P2 稱為 數據點,P1 稱為 控制點 。
具體python實現可以參考如下鏈接實現。
參考鏈接:
一種簡單的貝塞爾擬合算法
def computeBendingValue(p1,p2,p3):
''' 計算彎曲值 :param p1: :param p2: :param p3: :return: '''
return max(abs(p1[0]+p3[0]-2*p2[0]),abs(p1[1]+p3[1]-2*p2[1]))
def isSameGradient(p1,p2,p3):
''' 判斷相鄰三點是否在同一條直線上 :param p1: :param p2: :param p3: :return: '''
g1=(p1[1]-p2[1])/(p1[0]-p2[0]+0.00001)
g2=(p2[1]-p3[1])/(p2[0]-p3[0]+0.00001)
return g1==g2
計算拐點時,需要有些核心注意點:
計算筆跡端點的Bending value,需要進行一些預處理,我的處理如下:
#當位於左端點的時候
if i-k<0:
p1=pt[i]
else:
p1=pt[i-k]
#當位於右端點的時候
if i+k>=len(pt):
p3=pt[i]
else:
p3=pt[i+k]
如何計算自適應Bending value
k0=1
bv0=0
bv_list=[]
# 計算候選拐點所有的Bending Value曲率,直到最大值為止
while k0+i<len(pt) and i-k0>0:
bv0=computeBendingValue(pt[i-k0],pt[i],pt[i+k0])
if bv0>=bv:
bv_list.append(bv0)
bv=bv0
k0+=1
if bv0<bv:
break
k_list[i]=k0
# 計算所有曲率的平均值,作為最終的候選點的曲率
if len(bv_list)==0:
avg_bv=bv
else:
avg_bv=sum(bv_list)/len(bv_list)
進一步篩選拐點的實現
# 條件一:bv<theta.theta=1.1
# 條件二:bvi<bvj and j=i-1 or j=i+1,表示
# 條件三:bvi==bvi-1 and ki<ki-1
# 條件四:bvi==bvi+1 and ki<=ki+1
# 條件一表示Bending Value應該大於theta;條件二~四表示Bending Value應該為局部最大值
if avg_bv<1.1 or \
(curvs[i] < curvs[i - 1] or curvs[i] < curvs[i + 1]) or \
(curvs[i]==curvs[i-1] and k_list[i]<k_list[i-1]) or \
(curvs[i]==curvs[i+1] and k_list[i]<=k_list[i+1]):
continue
else:
result.append(i)
最後還需要進一步合並相鄰的拐點
merge_result=[]
i=0
tmp=[]
while i+1<len(result_1):
if result_1[i+1]-result_1[i]<5:
tmp.append(result_1[i])
if i+1==len(result_1)-1:
tmp.append(result_1[i+1])
merge_result.append(tmp)
tmp=[]
else:
tmp.append(result_1[i])
merge_result.append(tmp)
tmp=[]
if i + 1 == len(result_1) - 1:
merge_result.append([result_1[i+1]])
i=i+1
# 合並最終的結果
new_result=[]
for res in merge_result:
avg_res=sum(res)//len(res)
new_result.append(avg_res)
因為項目原因,不方便提供完整代碼,但核心點已經給出,方便大家參考。最終結果如下: