
匯總整理摘抄自
在圖像測量過程以及機器視覺應用中,為確定空間物體表面某點的三維幾何位置與其在圖像中對應點之間的相互關系,必須建立相機成像的幾何模型,這些幾何模型參數就是相機參數。在大多數條件下這些參數必須通過實驗與計算才能得到,這個求解參數(內參、外參、畸變參數)的過程就稱之為相機標定(或攝像機標定)。無論是在圖像測量或者機器視覺應用中,相機參數的標定都是非常關鍵的環節,其標定結果的精度及算法的穩定性直接影響相機工作產生結果的准確性。因此,做好相機標定是做好後續工作的前提,提高標定精度是科研工作的重點所在。
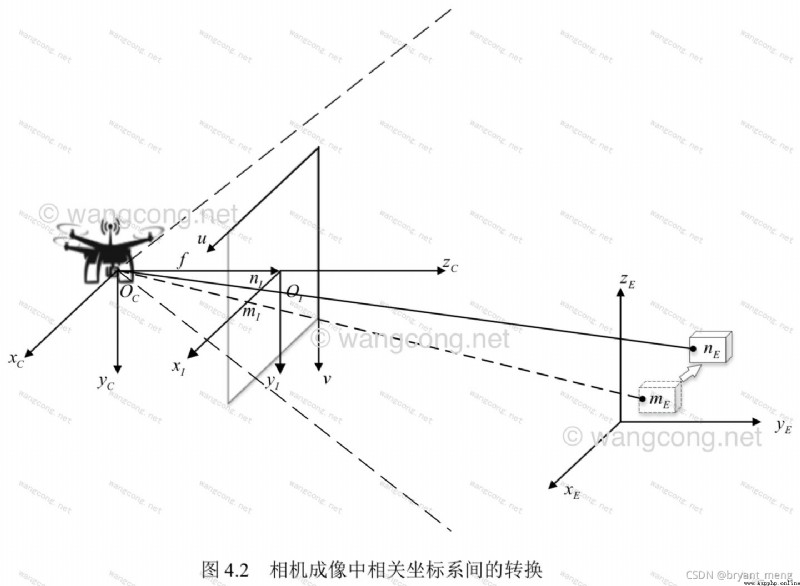
確定空間物體表面某點的三維幾何位置與其在拍攝圖像中對應點之間的相互關系涉及到了如下四個坐標系
像素平面坐標系 ( u , v ) (u,v) (u,v)
像平面坐標系(圖像物理坐標系) ( x , y ) (x,y) (x,y)
相機坐標系 ( X c , Y c , Z c ) (X_c,Y_c,Z_c) (Xc,Yc,Zc),camera coordinate system
世界坐標系 ( X w , Y w , Z w ) (X_w,Y_w,Z_w) (Xw,Yw,Zw),world coordinate system (wcs)
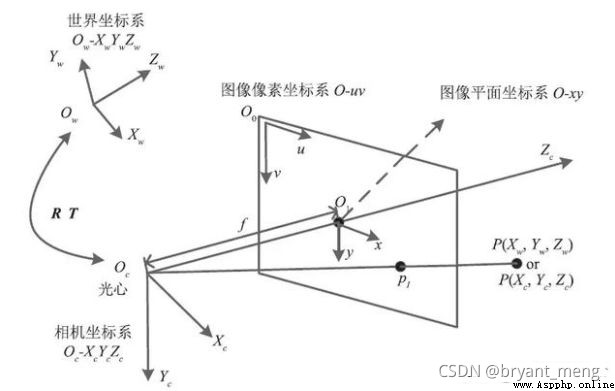
我們通過假設一些參數,使上面四個坐標系之間的坐標聯系起來,這樣我們就可以把拍攝的圖片上的一個點坐標反推導出世界坐標系中的那個點坐標,這樣就達到了三維重建的目的。

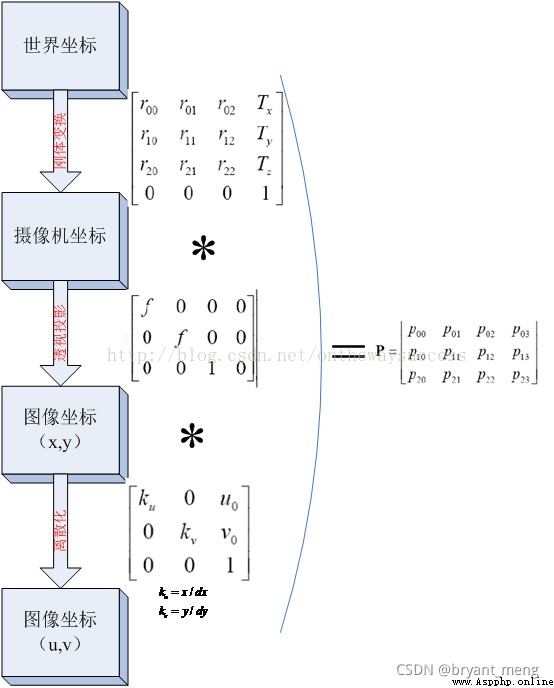
世界坐標系通過平移和旋轉(剛體變換)得到相機坐標系。相機坐標系通過成像模型中的相似三角形原理(透視投影)得到圖像坐標系。圖像坐標系通過平移和縮放得到像素坐標系。
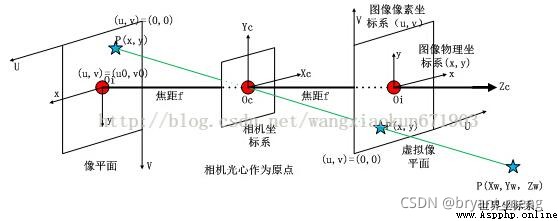
圖像物理坐標系 ( x , y ) (x,y ) (x,y):以相機光軸與成像平面的交點(principal point)為坐標原點,描述物體通過投影投射在成像平面中的位置(感光芯片上像素的實際大小),單位一般為 mm,屬於物理單位。
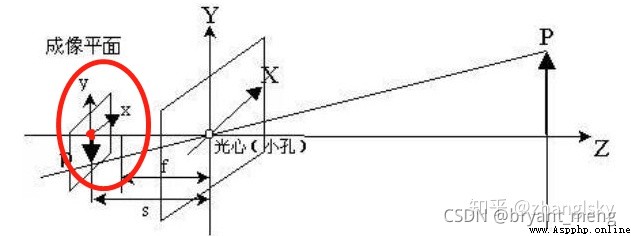
紅色圈出來的區域,即是圖像物理坐標系, 紅色的原點,可以記為圖像坐標系的原點。
像素坐標系 ( u , v ) (u,v ) (u,v):以成像平面左上頂點為坐標原點,為了描述像素點(pixel)在數字圖像中的坐標位置而引入。
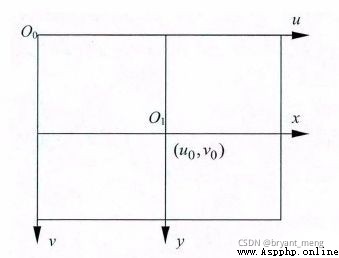
圖像坐標系與像素坐標系之間的轉換關系如下:
寫成矩陣形式:
再寫成齊次坐標形式:

其中, ( u , v ) (u,v ) (u,v) 表示像素的行數和列數, ( u 0 , v 0 ) (u_0,v_0 ) (u0,v0) 表示圖像坐標系原點在像素坐標系中的坐標, d x dx dx 和 d y dy dy 表示單個像素分別在 x x x 軸和 y y y 軸上的物理尺寸(單位為 mm/pixel),因而 x d x \frac{x}{dx} dxx 與 y d y \frac{y}{dy} dyy的單位為像素。
當然我們也可以表示成如下形式
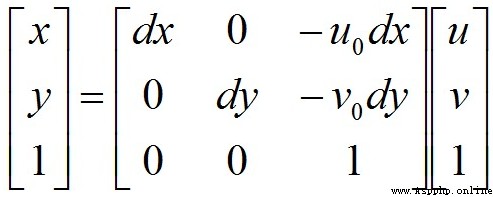
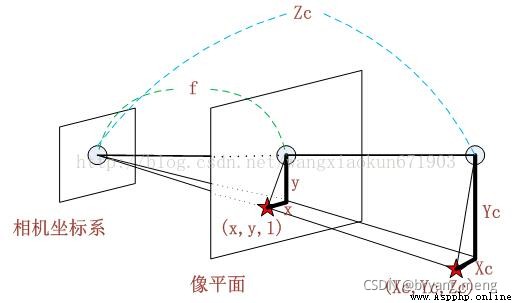
相機坐標系 ( X c , Y c , Z C ) (X_c,Y_c,Z_C ) (Xc,Yc,ZC):以相機的光心為坐標原點, [公式] 軸與相機光軸平行,單位為 mm
Z c Zc Zc 是指的圖像深度信息,每個像素點的 Z c Zc Zc 都會有差別
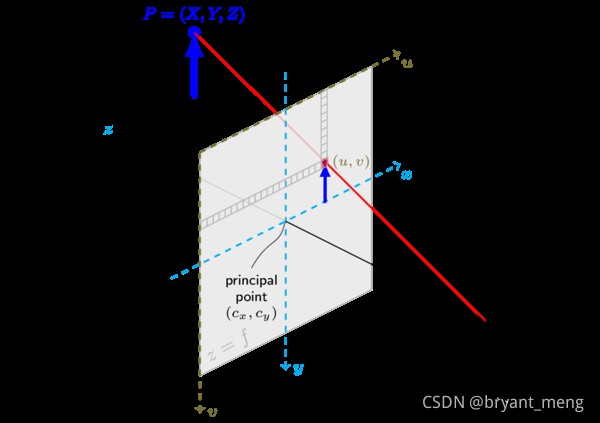
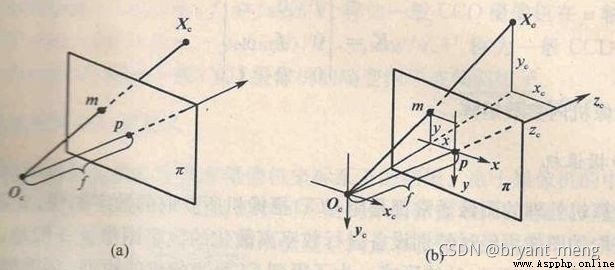

是不是老覺得上面這幾幅圖和小孔成像背離了,卡看下面這兩幅圖就柳暗花明,豁然開朗了
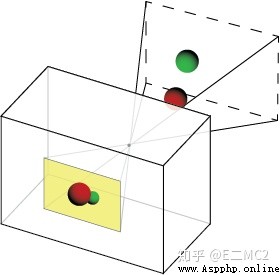
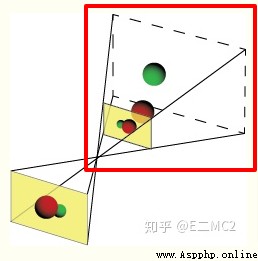
紅框部分也即
或者直接畫成這樣就會直觀很多
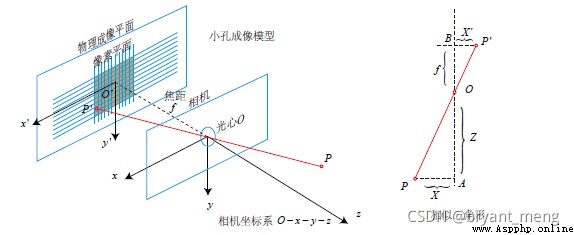
根據三角形相似原理可得:
整理可得:
寫成齊次坐標矩陣形式:

將像素坐標系與圖像坐標系的轉換公式帶入,可得:

整理可得:
其中, f x = f d x fx = \frac{f}{dx} fx=dxf , f y = f d y fy = \frac{f}{dy} fy=dyf 分別表示相機在 x x x 軸和 y y y 軸方向上的焦距,相機內參(Camera Intrinsic parameter) K K K 為:

世界坐標系 ( X W , Y W , Z W ) (X_W,Y_W,Z_W ) (XW,YW,ZW):
由於攝像機和物體可以安放在環境中的任何位置,因此需要在環境中選擇一個基准坐標系來描述攝像機的位置,並用它來描述環境中任何物體的位置,這個坐標系就叫做世界坐標系。
想將不同視點/視角拍攝的圖像信息整合在一起就必須將所有的信息放在同一個坐標系下,這個坐標系應與各張圖像的 相機/物體/像素 這些相對坐標系無關,在確定後應不變且唯一,即應為絕對坐標系,我們將這個坐標系稱為 世界坐標系 。
世界坐標系可以任意選擇,為假想坐標系,在被指定後隨即 不變且唯一,即為絕對坐標系
相機坐標的原點,可以是任意的相機位置(如下圖黃色框內),一般把相機的光心設置為相機坐標的原點,空間中 Z 軸與攝像機的光軸平行!

世界坐標系與相機坐標系之間為剛體變換的關系:

其中 [ R T 0 1 ] = [ r 11 r 12 r 13 t 1 r 21 r 22 r 23 t 2 r 31 r 32 r 33 t 3 0 0 0 1 ] \begin{bmatrix} R & T\\ 0 & 1 \end{bmatrix} = \begin{bmatrix} r_{11} & r_{12} & r_{13} & t1 \\ r_{21} & r_{22} & r_{23} & t2 \\ r_{31} & r_{32} & r_{33} & t3 \\ 0 & 0 & 0 & 1 \end{bmatrix} [R0T1]=⎣⎢⎢⎡r11r21r310r12r22r320r13r23r330t1t2t31⎦⎥⎥⎤
R、T 與攝像機無關,所以稱這兩個參數為攝像機的外參數 (extrinsic parameter)
下面詳細介紹下外參矩陣
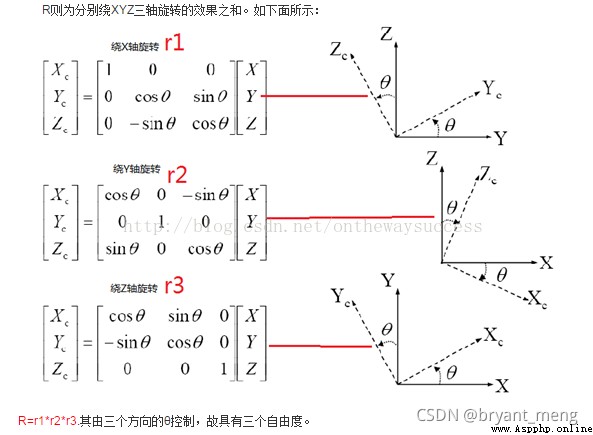
因為世界坐標系和像機坐標系都是右手坐標系,所以其不會發生形變。我們想把世界坐標系下的坐標轉換到像機坐標下的坐標,如下圖所示,可以通過剛體變換的方式。空間中一個坐標系,總可以通過剛體變換轉換到另外一個個坐標系的。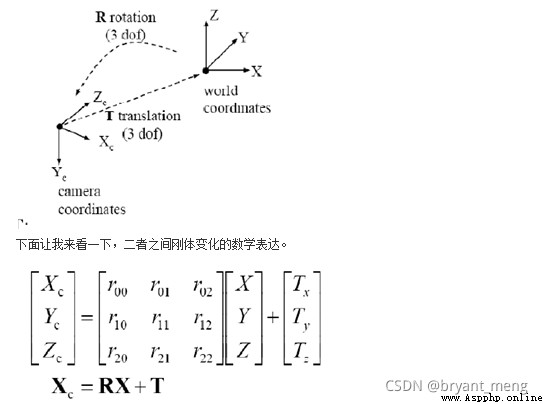
其中, X C X_C XC 代表攝像機坐標系, X X X 代表世界坐標系。 R R R 代表旋轉(因其受 x,y,z 三個方向上的分量共同控制,所以其具有三個自由度), T T T 代表平移
在實踐中,世界坐標系的選取可分為兩種情況,單目相機與雙目相機。
1,單目相機
在單目相機中,我們通常選擇拍攝第一張圖像時的相機坐標系作為世界坐標系,即以拍攝第一張圖像時相機的光心(小孔)作為原點,X 軸為水平方向,Y 軸為豎直方向,Z 軸指向拍攝第一張圖像時相機所觀察的方向。選定後世界坐標系便不再發生變化,即不變且唯一。
2,雙目相機
在雙目相機 (A,B) 中,與單目相機大同小異,我們可選取其中一個相機 A 拍攝第一張圖像時的相機坐標系為世界坐標系,即以相機 A 拍攝第一張圖像時相機的光心(小孔)作為原點,X 軸為水平方向,Y 軸為豎直方向,Z 軸指向拍攝第一張圖像時相機 A 所觀察的方向。
這樣的話 A 相機的 R 為單位矩陣,T 為零向量
這裡簡單的提及一些 opencv 庫方法
1)findChessboardCorners 和 drawChessboardCorners
找標定網格的角點,注意輸入需要是灰度圖
import cv2
img = cv2.imread(image)
h, w, _ = img.shape
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
ret, corners = cv2.findChessboardCorners(gray,(w,h),None) # 找角點, w 和 h 是標定表格每行每列的角點個數
cv2.drawChessboardCorners(img,(w,h), corners, ret) # 畫角點

參考 python+OpenCV 相機標定
2)getAffineTransform
根據兩張圖的三個對應點,求仿射變換矩陣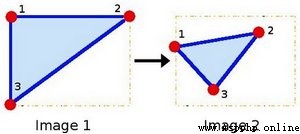
M = cv2.getAffineTransform(InputArray src, InputArray dst)
3)warpAffine
對圖片做變換生成新的圖片
cv2.warpAffine(src, M, dsize[, dst[, flags[, borderMode[, borderValue]]]]) → dst
參考 OpenCV 之 cv2.getAffineTransform + warpAffine
下面具體看看 flags 和 borderMode 有哪些可供選擇的
4)插值
插值方法,cv2.xxx opencv中插值算法詳解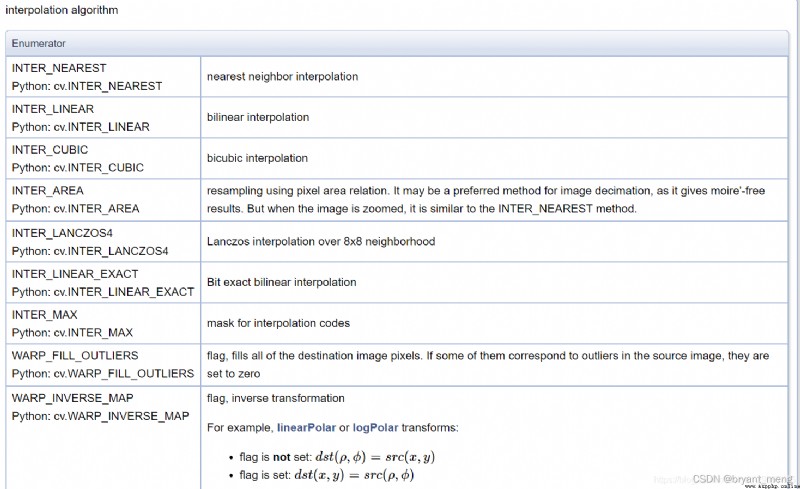
5)填充
填充方法 python-opencv 圖像通道分離,合並,邊界擴展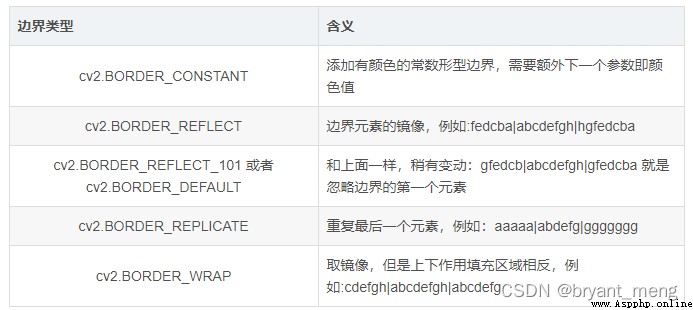
OpenCV庫成員——BorderTypes