General curvature calculation method , Such as Xuanchang proportional method 、 Three times B Spline expression 、 Linear polygon approximation and local symmetry . Today is mainly about Bending value algorithm （Bending value） Algorithm . The expression is ：
b i k = m a x ( ∣ ( x i − k − x i ) + ( x i + k − x i ) ) ∣ , ∣ ( y i − k − y i ) + ( y i + k − y i ) ∣ ) b_{ik}=max(|(x_{i-k}-x_{i})+(x_{i+k}-x_{i}))|,|(y_{i-k}-y_{i})+(y_{i+k}-y_{i})|) bik=max(∣(xi−k−xi)+(xi+k−xi))∣,∣(yi−k−yi)+(yi+k−yi)∣)
Calculation Bending Value The schematic diagram of is as follows ：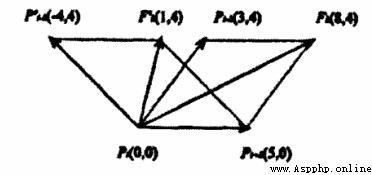
Reference link ：
Writing quality evaluation of handwritten Chinese characters
Calculate the Bending Value, Write it down as B v ( i ) Bv(i) Bv(i), Here you need to initialize the threshold delta=1.1 And search scope k=1
When B v ( i ) > d e l t a Bv(i)>delta Bv(i)>delta, And for all i − k < = j < = i + k i-k<=j<=i+k i−k<=j<=i+k, Both B v ( i ) > = B v ( j ) Bv(i)>=Bv(j) Bv(i)>=Bv(j), Then the point conforms to the property of maximum local curvature , As a candidate inflection point .
Screening condition 1 ： Judge three adjacent inflection points p i − 1 p_{i-1} pi−1、 p i p_{i} pi、 p i + 1 p_{i+1} pi+1 Whether it is on the same straight line , If it is, exclude this point
Screening condition 2 ： Calculate the adaptive bending value （Bending Value）. The algorithm flow is as follows ：
Calculate the search range of candidate points k from 1 Began to increase , use b i k b_{ik} bik At present Bending Value. If b i k > = b i k + 1 b_{ik}>=b_{ik+1} bik>=bik+1,k increase 1, Otherwise, stop increasing . Find continuous Bending Value After value , It is necessary to average again , As the bending value of the final point , The calculation formula is as follows ：
b v i = 1 k i ∑ j = 1 k i b i j b_{v_{i}}=\frac{1}{k_{i}}\sum^{k_{i}}_{j=1}b_{ij} bvi=ki1j=1∑kibij
According to the calculated adaptive inflection point , The following conditions also need to be met ：
Condition one means Bending Value The value should be greater than the threshold , Condition 2 、 3、 ... and 、 Four indicates that the inflection point must be a local maximum
After obtaining the points of the curve, there may be a large interval between points , We need to sample these points to increase their continuity . General sampling methods include DDA、 First order Bessel curve fitting 、 Quadratic Bessel curve fitting or cubic Bessel curve clutch . among DDA It is similar to the first-order Bessel curve fitting . Both are sampled by the slope of the straight line between two points , Of course, use higher-order methods , The sampling curve is also smoother .
As shown in the figure above , For two points on the plane P0 and P1, Suppose another point B From P0 Move to P1 spot , Then there are B The point is t The coordinate formula of time ：
take B The line formed by connecting the coordinates of points at each time in turn , Is the so-called Bezier curve . This formula represents a Bessel curve , Also known as linear Bessel curve .
python The implementation is as follows ：
def getFirstBezierPointByT(start,end,t):
''' Calculate the coordinate value of each time according to the calculation formula of the first bell curve :param start: :param end: :param t: :return: '''
x=(1-t)*start[0]+t*end[0]
y=(1-t)*start[1]+t*end[1]
return [x,y]
def calculateFirstBezierPoints(start,end):
''' Calculate the set of Searle curve points between two points :param start: :param handle: :param end: :return: '''
bx=start[0]
by=start[1]
ex=end[0]
ey=end[1]
beDis=math.sqrt(math.pow((bx-ex),2)+math.pow((by-ey),2))
count=int(beDis//1)
if count<2:
return [start]
step = 1.0 / count
points=[]
t = 0.0
for i in range(count):
points.append(getFirstBezierPointByT(start, end, t))
t += step
return points
def firstBezierCurveFitting(pts):
''' First order Bessel curve fitting :param pts: :return: '''
new_pts = []
for pt in pts:
new_pt = []
for i in range(0, (len(pt) - 1)):
pp=calculateFirstBezierPoints(pt[i], pt[i + 1])
new_pt += pp
new_pt.append(pt[len(pt)-1])
new_pts.append(new_pt)
return new_pts
similarly , For three points on the plane P0、P1 and P2 , hypothesis P0P1 There is a point between B1 From P0 Moving to P1 ,P1P2 There is a point between B2 From P1 Moving to P2, Then there are ：
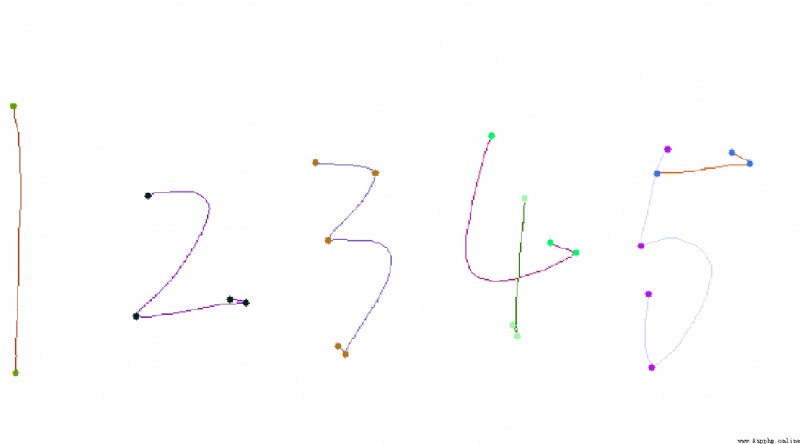
Suppose another point B From B1 Moving to B2, Then there are B Coordinate formula of point ：
take B1 and B2 The coordinate formula of is substituted into the above expression , After finishing, we get B Coordinate formula of point ：
B The curve formed by the coordinates of points at each time is called quadratic Bessel curve , among P0 and P2 be called The data points ,P1 be called The control points .
Specifically python For implementation, please refer to the following link .
Reference link ：
A simple Bessel fitting algorithm
def computeBendingValue(p1,p2,p3):
''' Calculate the bending value :param p1: :param p2: :param p3: :return: '''
return max(abs(p1[0]+p3[0]-2*p2[0]),abs(p1[1]+p3[1]-2*p2[1]))
def isSameGradient(p1,p2,p3):
''' Judge whether the adjacent three points are on the same straight line :param p1: :param p2: :param p3: :return: '''
g1=(p1[1]-p2[1])/(p1[0]-p2[0]+0.00001)
g2=(p2[1]-p3[1])/(p2[0]-p3[0]+0.00001)
return g1==g2
When calculating the inflection point , There are some core considerations ：
Calculate the end of the handwriting Bending value, Some pretreatment is needed , My treatment is as follows ：
# When at the left endpoint
if i-k<0:
p1=pt[i]
else:
p1=pt[i-k]
# When at the right end
if i+k>=len(pt):
p3=pt[i]
else:
p3=pt[i+k]
How to calculate adaptivity Bending value
k0=1
bv0=0
bv_list=[]
# Calculate all of the candidate inflection points Bending Value Curvature , Up to the maximum
while k0+i<len(pt) and i-k0>0:
bv0=computeBendingValue(pt[i-k0],pt[i],pt[i+k0])
if bv0>=bv:
bv_list.append(bv0)
bv=bv0
k0+=1
if bv0<bv:
break
k_list[i]=k0
# Calculate the average of all curvature , The curvature of the final candidate point
if len(bv_list)==0:
avg_bv=bv
else:
avg_bv=sum(bv_list)/len(bv_list)
Further screening inflection point implementation
# Conditions for a ：bv<theta.theta=1.1
# Condition 2 ：bvi<bvj and j=i-1 or j=i+1, Express
# Condition 3 ：bvi==bvi-1 and ki<ki-1
# Condition 4 ：bvi==bvi+1 and ki<=ki+1
# Condition one means Bending Value Should be greater than theta; Condition 2 ~ Four representations Bending Value It should be a local maximum
if avg_bv<1.1 or \
(curvs[i] < curvs[i - 1] or curvs[i] < curvs[i + 1]) or \
(curvs[i]==curvs[i-1] and k_list[i]<k_list[i-1]) or \
(curvs[i]==curvs[i+1] and k_list[i]<=k_list[i+1]):
continue
else:
result.append(i)
Finally, we need to further merge adjacent inflection points
merge_result=[]
i=0
tmp=[]
while i+1<len(result_1):
if result_1[i+1]-result_1[i]<5:
tmp.append(result_1[i])
if i+1==len(result_1)-1:
tmp.append(result_1[i+1])
merge_result.append(tmp)
tmp=[]
else:
tmp.append(result_1[i])
merge_result.append(tmp)
tmp=[]
if i + 1 == len(result_1) - 1:
merge_result.append([result_1[i+1]])
i=i+1
# Merge the final results
new_result=[]
for res in merge_result:
avg_res=sum(res)//len(res)
new_result.append(avg_res)
Because of the project , It is not convenient to provide complete code , But the core point has been given , For your reference . The final results are as follows ：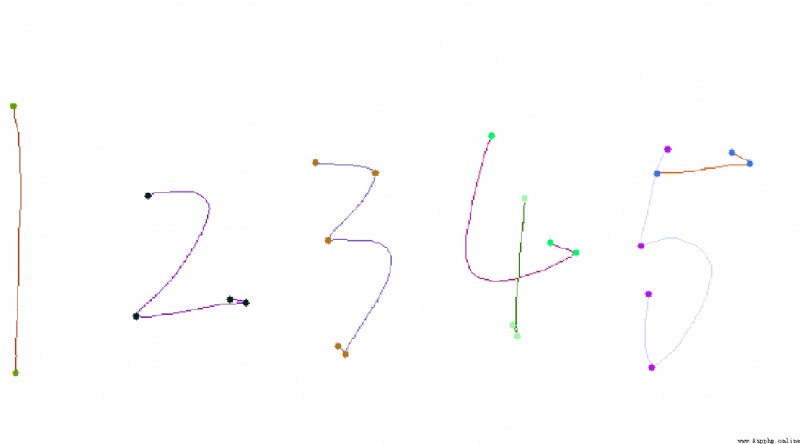
Python & c++ mixed call programming comprehensive practice -16c++ calls Pythons class instantiation object to access member functions and members
author ： Empty bad uncle Blog
Python報：lxml.etree.XMLSyntaxError Opening and ending tag mismatch meta line 4 and head, line 6
【Python】報：lxml.etree.XMLSyntax
