List of articles

• One 、 Realization principle
• • 1.1、 Calculate the distance from the point to the line —— Helen's formula
  • 1.2、 Arch height and chord length calculation radius
• Two 、python Realize curvature calculation

Recently, we need to make a rough estimate of the curvature of the curve , Record it here . In fact, the calculation of curvature is to find the radius corresponding to this arc length , in other words , Let's look at the curve as the arc length of a circle , So the question is simple .

One 、 Realization principle

1.1、 Calculate the distance from the point to the line —— Helen's formula

As shown in the figure below , To calculate A To CB The length of .

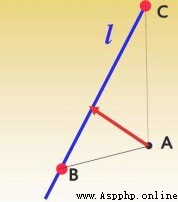
set up Δ \Delta ΔABC The three sides of the are a,b,c, Then Helen's formula calculates the area S as follows ：
S = p ( p − a ) ( p − b ) ( p − c ) Its in : p = 1 2 ( a + b + c ) S=\sqrt{p(p-a)(p-b)(p-c)} \\ among : p=\frac{1}{2}(a+b+c) S=p(p−a)(p−b)(p−c)​ Its in :p=21​(a+b+c)
take p Bring in Helen's formula , have to ：
S = 1 4 ( a + b + c ) ( a + b − c ) ( a + c − b ) ( b + c − a ) S=\frac{1}{4}\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)} S=41​(a+b+c)(a+b−c)(a+c−b)(b+c−a)​
As shown in the figure below ,AD yes A The straight line BC Distance of , That is AD yes Δ \Delta ΔABC edge BC It's high up there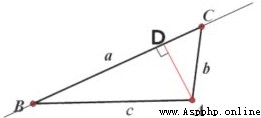

S = a ∗ A D 2 S=\frac{a*AD}{2} S=2a∗AD​
namely ：
1 4 ( a + b + c ) ( a + b − c ) ( a + c − b ) ( b + c − a ) = a ∗ A D 2 \frac{1}{4}\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}=\frac{a*AD}{2} 41​(a+b+c)(a+b−c)(a+c−b)(b+c−a)​=2a∗AD​

Merge to get ：
A D = 1 2 a ( a + b + c ) ( a + b − c ) ( a + c − b ) ( b + c − a ) AD=\frac{1}{2a}\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)} AD=2a1​(a+b+c)(a+b−c)(a+c−b)(b+c−a)​

1.2、 Arch height and chord length calculation radius

As shown in the figure , We know the chord length L And bow height H, Requirements R. We can get it according to Pythagorean theorem of triangle .

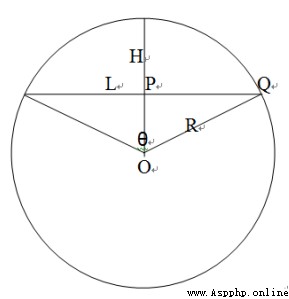
For right triangle OPQ,OP=R-H,OQ=R,PQ= L 2 \frac{L}{2} 2L​, Then the calculation is as follows ：
R 2 = ( L 2 ) 2 + ( R − H ) 2 R 2 = L 4 4 + R 2 − 2 R H + H 2 2 R H = L 4 4 + H 2 R = L 2 4 + H 2 2 H R^{2}=(\frac{L}{2})^{2}+(R-H)^{2} \\ R^{2}= \frac{L^{4}}{4}+R^{2}-2RH+H^{2} \\ 2RH=\frac{L^{4}}{4}+H^{2} \\ R=\frac{\frac{L^{2}}{4}+H^{2}}{2H} R2=(2L​)2+(R−H)2R2=4L4​+R2−2RH+H22RH=4L4​+H2R=2H4L2​+H2​

Two 、python Realize curvature calculation

import numpy as np
def get_arc_curve(pts):
''' Get radian value :param pts: :return: '''
# Calculate chord length 
start = np.array(pts[0])
end = np.array(pts[len(pts) - 1])
l_arc = np.sqrt(np.sum(np.power(end - start, 2)))
# Calculate the maximum distance from the point on the arc to the line 
# Calculation formula ：\frac{1}{2a}\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}
a = l_arc
b = np.sqrt(np.sum(np.power(pts - start, 2), axis=1))
c = np.sqrt(np.sum(np.power(pts - end, 2), axis=1))
dist = np.sqrt((a + b + c) * (a + b - c) * (a + c - b) * (b + c - a)) / (2 * a)
h = dist.max()
# Calculate curvature 
r = ((a * a) / 4 + h * h) / (2 * h)
return r
if __name__ == '__main__':
x = np.linspace(1, 100, 99).astype(np.int64)
y = (x ** 2)
xy = list(zip(x, y)) # list of points in 2D space
print(get_arc_curve(xy))

Refer to the connection ：

How to calculate the radius of a long bow with strings

【 Programming 】 Quickly calculate the distance from a point to a straight line , Don't use oblique

OpenCV： Simply calculate the curve radian - Bow radian