如下圖所示,要計算A到CB的長度。
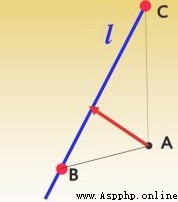
設 Δ \Delta ΔABC的三條邊分別為a,b,c,那麼海倫公式計算面積S如下:
S = p ( p − a ) ( p − b ) ( p − c ) 其 中 : p = 1 2 ( a + b + c ) S=\sqrt{p(p-a)(p-b)(p-c)} \\ 其中: p=\frac{1}{2}(a+b+c) S=p(p−a)(p−b)(p−c)其中:p=21(a+b+c)
將p帶入海倫公式,得:
S = 1 4 ( a + b + c ) ( a + b − c ) ( a + c − b ) ( b + c − a ) S=\frac{1}{4}\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)} S=41(a+b+c)(a+b−c)(a+c−b)(b+c−a)
如下圖所示,AD是A到直線BC的距離,即是AD是 Δ \Delta ΔABC邊BC上的高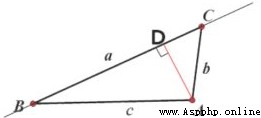
S = a ∗ A D 2 S=\frac{a*AD}{2} S=2a∗AD
即:
1 4 ( a + b + c ) ( a + b − c ) ( a + c − b ) ( b + c − a ) = a ∗ A D 2 \frac{1}{4}\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}=\frac{a*AD}{2} 41(a+b+c)(a+b−c)(a+c−b)(b+c−a)=2a∗AD
合並可以得:
A D = 1 2 a ( a + b + c ) ( a + b − c ) ( a + c − b ) ( b + c − a ) AD=\frac{1}{2a}\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)} AD=2a1(a+b+c)(a+b−c)(a+c−b)(b+c−a)
如圖所示,我們已知了弦長L和弓高H,需要求R。我們可以根據三角形得勾股定理求得。
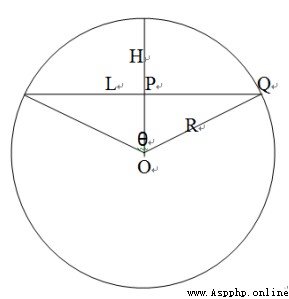
對於直角三角形OPQ,OP=R-H,OQ=R,PQ= L 2 \frac{L}{2} 2L,那麼計算如下:
R 2 = ( L 2 ) 2 + ( R − H ) 2 R 2 = L 4 4 + R 2 − 2 R H + H 2 2 R H = L 4 4 + H 2 R = L 2 4 + H 2 2 H R^{2}=(\frac{L}{2})^{2}+(R-H)^{2} \\ R^{2}= \frac{L^{4}}{4}+R^{2}-2RH+H^{2} \\ 2RH=\frac{L^{4}}{4}+H^{2} \\ R=\frac{\frac{L^{2}}{4}+H^{2}}{2H} R2=(2L)2+(R−H)2R2=4L4+R2−2RH+H22RH=4L4+H2R=2H4L2+H2
import numpy as np
def get_arc_curve(pts):
''' 獲取弧度值 :param pts: :return: '''
# 計算弦長
start = np.array(pts[0])
end = np.array(pts[len(pts) - 1])
l_arc = np.sqrt(np.sum(np.power(end - start, 2)))
# 計算弧上的點到直線的最大距離
# 計算公式:\frac{1}{2a}\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}
a = l_arc
b = np.sqrt(np.sum(np.power(pts - start, 2), axis=1))
c = np.sqrt(np.sum(np.power(pts - end, 2), axis=1))
dist = np.sqrt((a + b + c) * (a + b - c) * (a + c - b) * (b + c - a)) / (2 * a)
h = dist.max()
# 計算曲率
r = ((a * a) / 4 + h * h) / (2 * h)
return r
if __name__ == '__main__':
x = np.linspace(1, 100, 99).astype(np.int64)
y = (x ** 2)
xy = list(zip(x, y)) # list of points in 2D space
print(get_arc_curve(xy))
參考連接:
有弦長弓高怎麼算半徑
【編程】快速計算點到直線距離,不用點斜式
OpenCV:簡單計算曲線弧度-弓形弧度