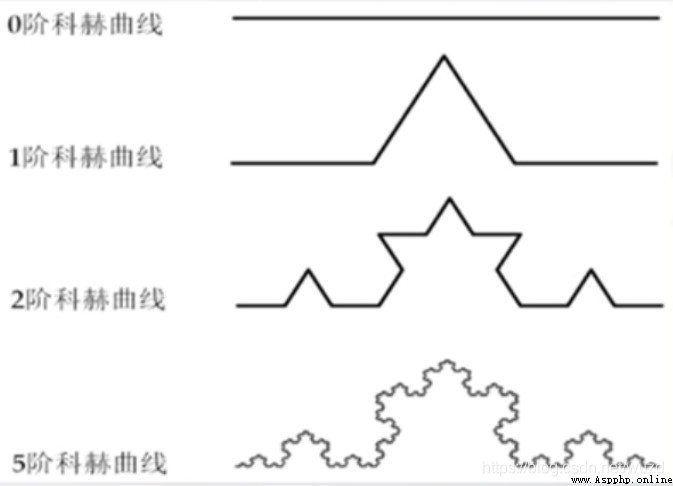
Koch curve is a kind of fractal . Its shape is like snow , Also known as Koch snow 、 Snow curve .
1. Given line segments AB, Koch curve can be generated by the following steps :
2. Divide the line segment into three equal parts (AC,CD,DB)
3. With CD Bottom , outward ( Casual inside and outside ) Draw an equilateral triangle DMC
4. Put the line segment CD Remove , Respectively for AC,CM,MD,DB repeat 1~3.
import turtle
# Koch curve (size The length of each straight line of koch curve ,n Degree of drawing )
def koch(size,n):
if n==0:# The recursive exit draws a first-order line
turtle.fd(size)
else:
# Each layer recursively traverses these four angles
for angle in [0,60,-120,60]:
# Turn the angle counter clockwise
turtle.left(angle)
# Recursively call itself
koch(size/3,n-1)
def snow(a):
#turtle.color("green","yellow")
turtle.begin_fill()
# When width and height are integers , Represents pixels
turtle.screensize(600,600,"green")
# Fill the border and the middle color
turtle.color("gold","white")
# Brush up
turtle.penup()
# The width of the brush
turtle.pensize(2)
# Reach the specified location
turtle.goto(-200,100)
# Brush down , Start writing
turtle.pendown()
#a=1 #1 rank koch curve
# First jumper 0 It's time to start , Clockwise 120 Degree end draw
koch(400,a)
# Second jumper 120 It's time to start , Clockwise 240 Degree end
turtle.right(120)
# Second jumper draw
koch(400,a)
# The third jumper 240 It's time to start , Clockwise 360 Degree end
turtle.right(120)
# The third jumper draw
koch(400,a)
# Filling complete
turtle.end_fill()
# Hide the brush
turtle.hideturtle()
# Enter the number of layers of koch curve
n=input(' Please enter koch The number of layers of the curve (1):\n') #n rank koch curve
if n=='': # Without input ,1 rank koch curve
n=1
# Main function execution
snow(int(n))
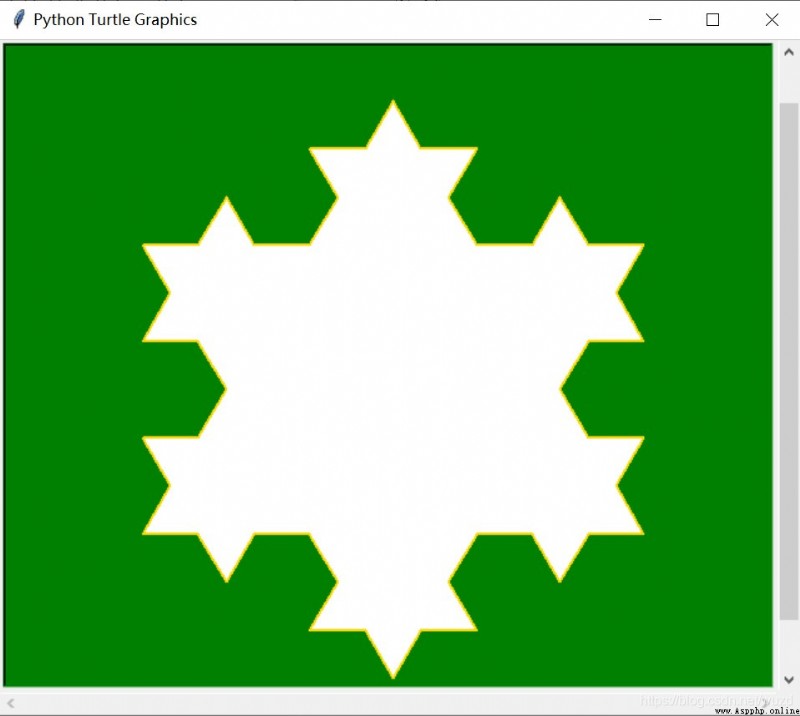
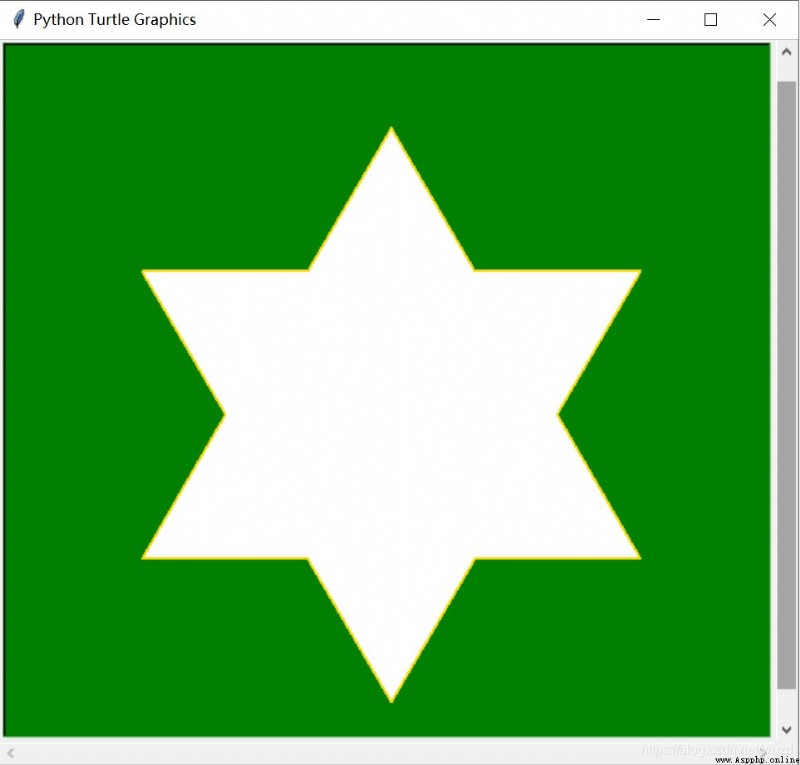
Please enter koch The number of layers of the curve (1):1
Please enter koch The number of layers of the curve (1):2