At the same time, they are preparing for the Blue Bridge Cup If there are deficiencies in the solution, please criticize and correct
Freshmen are not undergraduate students
The goal is to enter a large factory
Luogu ： Kinship Topic link
Problem analysis ： This is a classic example of investigating and searching collections .
What is a joint search set ？ Parallel search set is a kind of （ Tree shape ） data structure , Used to deal with some Disjoint sets Merge And Inquire about problem .
thought ： The whole forest is represented by an array , The root node of the tree uniquely identifies a collection , We just find the root of an element , You can determine which set it is in .
For example, give an array parent=[0,1,5,1,3,1],parent[i] Represents a node i The parent node （ It's very image ！？）
Look at the array , We know :parent[2]=5 , Explains the node 2 The parent of is 5
Come again ：parent[5]=1, Explains the node 5 The parent of is 1
Come again :parent[1]=1, Explains the node 1 The parent of is 1
You may have doubts about the above line ： Let's first remember , if parent[i]=i be i yes The root node in a collection
So what role does he play ： If a node j Its parent node's parent node's parent node's parent node ..... yes i
Illustrates the j And its parent node and its parent node and .... There are so many nodes , For each node , You can access i node . We might as well call it ancestor （ Be able to access Be similar to It is related by blood , You and your ancestors , Your father's ancestors , Your father's father's ancestors are related by blood .）
Therefore, so many nodes form a set （ The object representing the collection is the root node （ The ancestors ））
So for the array just mentioned , Due to the node 5 You can access ancestors >>1, therefore 5 and 1 Be related by blood , namely 5 Belong to ancestors 1 Represents a collection of , Due to the node 2 The parent of is 5, So it can pass through the parent node 5 Visit ancestors >>1, therefore 2 and 1 Be related by blood , namely 2 Belong to ancestors 1 Represents a collection of .
Therefore, we need to judge whether the two nodes belong to the same set , It can be judged by visiting their ancestors .
If the ancestors are the same , Then it belongs to the same set , Otherwise, it does not belong to the same set .
For the above array nodes 0 And the nodes 1 Does not belong to the same set
So here is the code for accessing ancestors :（ Optimization will be described below ）
def find_root(x):
while x!=parent[x]:3 If it weren't for our ancestors Just visit your parent node
x=parent[x]
return xSo the above code represents one of the ideas of joint search ： Inquire about
Now let's study another idea of searching sets ： Merge
Give the above example again parent=[0,1,5,1,3,1]
We know the node 1,2,3,4,5 Belong to the same set （ Use node 1 To mark ）
because parent[0]=0 explain 0 Is the ancestor of a collection , This set uses nodes 0 To mark
Because of the node 0 The number of set elements represented by is 1, A special , We might as well give it to him （ aggregate ） Add two nodes
They are nodes 6, node 7, therefore parent=[0,1,5,1,3,1,0,0]
So now node 0,6,7 Belong to the same set （ Use node 0 To mark ）
Next, we will study merger , What is a merger ？ Is to change two sets into one set
So what's the use of this ： We know to use nodes 0 To identify the nodes in the set , Can access the node 0, Now the node 0 You can also access the node 1, So use nodes 0 To identify the nodes in the set , Can access the node 1, So use nodes 1 To identify the set The number of nodes has expanded ！ Isn't this exactly what we want ？
in short aggregate A And collection B Originally, they belonged to two families , hold A Our ancestors as B Children of ancestors , So set A and B All nodes in are related by blood , Achieved family merger .
So here is the merged code ：
def union(x,y):# Merge
x_root,y_root=find(x),find(y)
parent[x_root]=y_root# General x_root!=y_root, Directly merge the past
# If x_root=y_root, Merge itself , Nothing has changed
therefore The code can be written ：
def find_root(x):
while x!=parent[x]:
x=parent[x]
return x
def union(x,y):
x_root=find_root(x)
y_root=find_root(y)
parent[x_root]=y_root
n,m,p=map(int,input().strip().split())
parent=[i for i in range(n+1)]# initialization
for i in range(m):#h Merge
tmp=list(map(int,input().strip().split()))
union(tmp[0],tmp[1])
for j in range(n):# Judge
tmp=list(map(int,input().strip().split()))
if find_root(tmp[0])==find_root(tmp[1]):
print('Yes')
else:
print('No')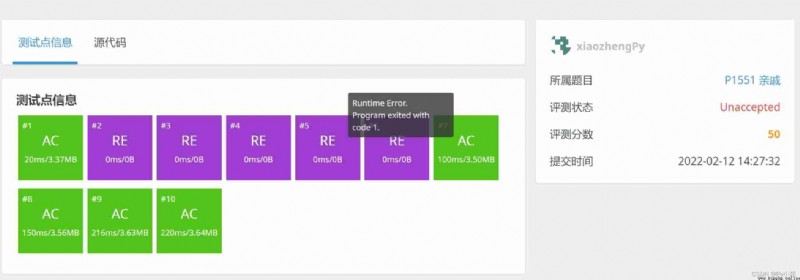
But this timeout So it needs to be optimized ：
First analyze the reason for the timeout ： Or use the array given above parent=[0,1,5,1,3,1,0,0]（ Unconsolidated ）
We can draw the following diagram ：
So scientists have come up with a way ： Path compression .
in short , For the picture above , Like visiting 4 When the root node of , After the '' For a long '' A path , This path consists of many nodes , They have a common feature that the root nodes are 1, So what path compression needs to do is to set the parent node of all nodes on this path as nodes 1
The function of such a son ： For example, my next query node 3 When the root node of , It only needs 1 Time , The original need 9999 Time ！
def find_root(x):# Return root node
if x!=parent[x]:# As long as it's not the root node
parent[x]=find_root(parent[x])# Change the parent node to the root node
return parent[x]# Return root node ( Parent node )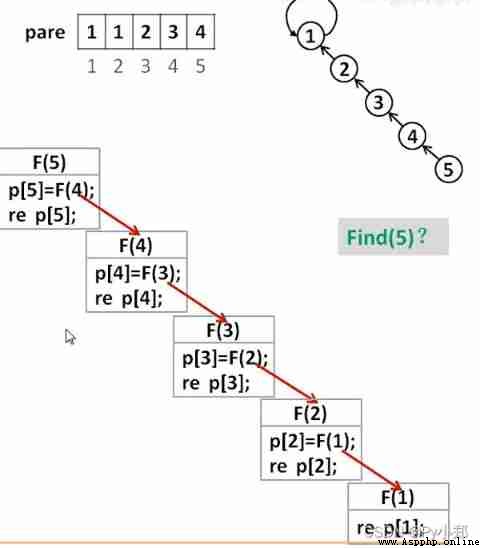
The first contact path compression is not easy to understand , You can write down this template like Xiao Zheng ~
n,m,p=map(int,input().strip().split())
parent=[i for i in range(n+1)]
def find_root(x):# Return root node
if x!=parent[x]:# As long as it's not the root node
parent[x]=find_root(parent[x])# hold x The parent node of is set as the root node
return parent[x]
def union(x,y):
x_root=find_root(x)
y_root=find_root(y)
parent[x_root]=y_root
for i in range(m):
tmp=list(map(int,input().strip().split()))
union(tmp[0],tmp[1])
for j in range(p):
tmp=list(map(int,input().strip().split()))
if find_root(tmp[0])==find_root(tmp[1]):
print('Yes')
else:
print('No')
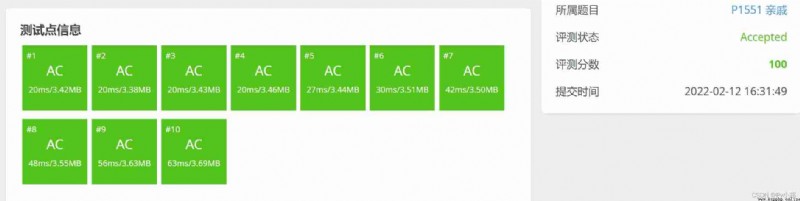
Visible path compression helps us optimize the algorithm
Blue Bridge Cup real battle ： Seven segment code （ The 11th exam questions E Fill in the blank and press the shaft ）>> Investigate Union checking set
Code design analysis : The question is about connectivity , from 7 Select several edges to judge whether it is a connected graph .
That is, to judge whether it belongs to the same set . First of all, make it clear , And search two functions ： Find and merge . To merge first , To find the （ What can I find without merging a set ？）. therefore , It's equivalent to building a kinship network first , Finally, judge whether the ancestors of all nodes are the same , If yes, then connect , Otherwise it's not connected .
Then the conditions for building kinship ： If two vertices are directly connected , Then merge the set of that point with the set of another point . When all the points are merged , Just traverse the ancestors of all points , Judge whether they are all the same , If it is , Be accomplished ,count Add 1
def find_root(x):
if x!=parent[x]:
parent[x]=find_root(parent[x])
return parent[x]
def union(x,y):
x_root,y_root=find_root(x),find_root(y)
if x_root!=y_root:
parent[x_root]=y_root
edge=[[0]*7 for i in range(7)]# Set a 0 Go in on the fifth , Boundless is connected with it
l=[0,1,2,3,4,5,6]
edge[0][1]=edge[0][2]=edge[1][3]=edge[1][4]=edge[2][3]=1
edge[3][4]=edge[3][5]=edge[4][6]=edge[5][6]=edge[2][5]=1# There are edges connected as 1
for i in range(7):
for j in range(7):
edge[i][j]=max(edge[i][j],edge[j][i])# Undirected graph symmetry
import itertools
count=0
for i in range(1,8):# Number of bulbs
for j in itertools.combinations(l,i):# such as [(1,2,3),[1,2,4]]
parent=[i for i in range(7)]
# Judge whether the two are connected
for k in range(0,i):
for p in range(k+1,i):
if edge[j[k]][j[p]]==1:# If it's connected , Merge
union(j[k],j[p])
for m in range(i-1):# Determine whether it belongs to the same set （ In the end, all ）
if find_root(j[m])!=find_root(j[m+1]):
break
else:
print(j)# Display eligible data , Delete
count+=1
print(count)
# answer 80I'm Xiao Zheng Is running to love Go to the mountains and seas ！
