Least square curve fitting of arbitrary order and python class implementation

Least square curve fitting of any order and Python Class implementation

The full text pictures and code are transferred from ：https://amphenol-sensors.cn/newsinfo/3017644.html

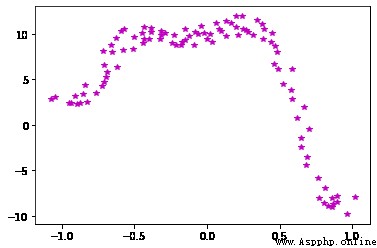
chart -1 Schematic diagram of analog input and output acquisition signal

The full text content can be inquired on the original website . But the feature of this code is to create classes , And the fitting order can be input arbitrarily （ If there is any result, let's say otherwise , Look at the actual input data ）. The following is further simplified , After all, code and description are the most important .

（1） This is the formula set by the final fitting ：

（2-0） This is the well-known deviation formula , If this sum of squares formula has a minimum , Then you can get the above coefficient

（2-1） This is the content after the above deviation formula is substituted

（3-1） The necessary condition for the minimum value of the above deviation formula

（3-2） Simplification of the above necessary conditions （ Numerous ？）

（3-3）3-2 The leftmost matrix decomposition in

（3-4）3-2 The actual composition of the rightmost matrix in

（4） The final calculation form of the fitting coefficient matrix needs to be solved

Python Realize least square curve fitting

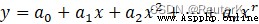
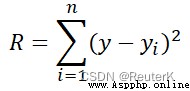
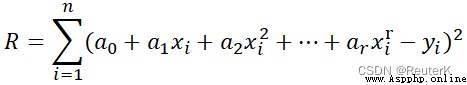
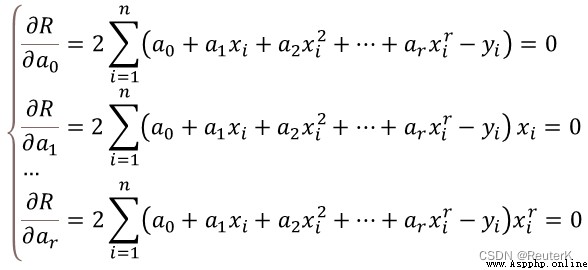
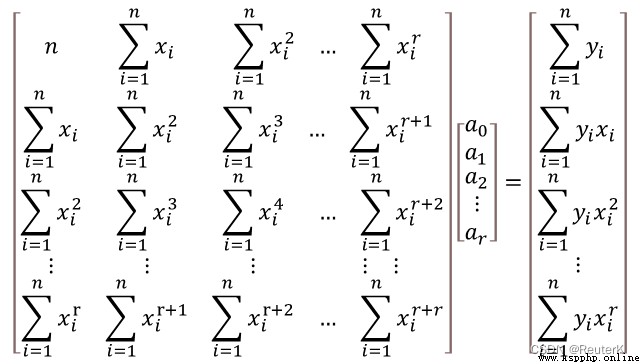
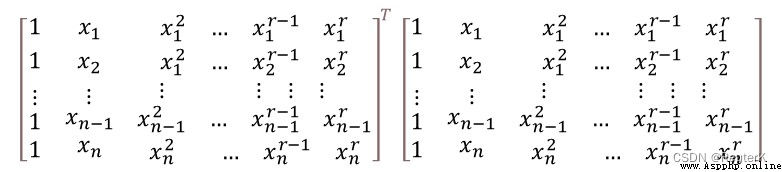
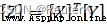
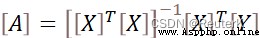
The result equation of output curve fitting （9 Order fitting ）

Function(x)=9.798298367046073+4.227514414846013x+17.260341567511098x**2-22.3475762650598x**3-128.91239180578455x**4-46.45306126416519x**5+152.35732377108258x**6+126.51471748420587x**7-53.97163898194201x**8-67.97621051238404x**9

Specify the range and resolution to output the graph after curve fitting （ You can use the default values ）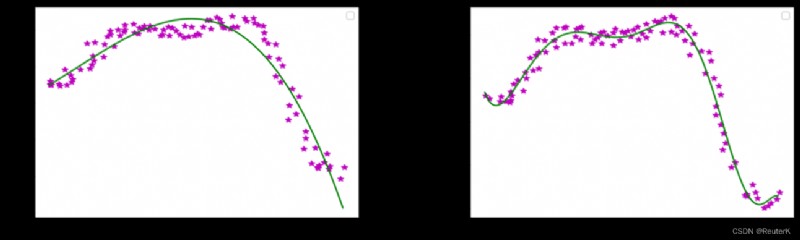

3 Order fitting （ left ） and 9 Order fitting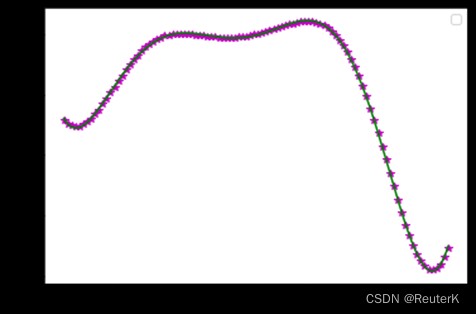

Ideal curve output

import matplotlib.pyplot as plt
import math
import numpy
import random
class LeastSqauresCF():
def __init__(self):
self.order = 1
self.Xvalues = None
self.Yvalues = None
self.fig = plt.figure()
self.subfig = self.fig.add_subplot(111)
#========================================
# Draw the input points/curve in a figure
#========================================
def ReadAnddrawInputPoints(self,Inputx=None,InputY=None, order=1):
try:
if Inputx is None or InputY is None:
return False
if(len(Inputx)!=len(InputY)):
return False
if order <=0:
return False
if type(order) !=int:
self.order = int(order)
else:
self.order = order
self.Xvalues = Inputx
self.Yvalues = InputY
self.subfig.plot(Inputx,InputY,color='m',linestyle='',marker='*')
return True
except Exception as e:
print(e)
return False
#========================================
# Calculate curve fitting factor matrix
#======================================== 
def produceFittingCurveFactors(self):
try:
#(1) Generate matrix [X]
matX=[]
for i in range(0,len(self.Xvalues)):
matx1=[]
for j in range(0,self.order+1):
dx=1.0
for l in range(0,j):
dx = dx * self.Xvalues[i]
matx1.append(dx)
matX.append(matx1)
#(2) Generate matrix [X]T.[X]
matX_Trans = numpy.matrix(matX).T
matX_FinalX = numpy.dot(numpy.matrix(matX_Trans),numpy.matrix(matX))
#(3) Generate matrix Y' =[X]T.[Y]
matFinalY = numpy.dot(matX_Trans,numpy.matrix(self.Yvalues).T)
#(4) Solve the function:[A] = [[X]T.[X]]**(-1).[X]T.[Y]
matAResult=numpy.linalg.solve(numpy.array(matX_FinalX),numpy.array(matFinalY))
return matAResult
except Exception as e:
print(e)
return None
#========================================
# Output fitting curve function
#======================================== 
def outputFittingCurveFunction(self, inputMatFactors=None):
if inputMatFactors is None:
return False
i = 0
strFitting="Function(x)="
for a in inputMatFactors:
#print(a[0])
if i==0:
strFitting +=str(a[0])
else:
strFitting +=("+"if a[0]>0 else"") +str(a[0])+(("x**"+str(i)) if i>1 else "x")
i+=1
print(strFitting)
return strFitting
#========================================
# draw the curve based on the result function
#========================================
def drawFittedCurve(self, xRangeMin=None,xRangeMax=None,matAResult=None,resolution=0.01):
try:
if matAResult is None:
return False
if xRangeMin is None or xRangeMax is None:
xRangeMin = self.Xvalues[0]
xRangeMax = self.Xvalues[-1]
#print('xRangeMin: ',xRangeMin, 'xRangeMax: ',xRangeMax)
xxa= numpy.arange(xRangeMin,xRangeMax,resolution)
yya=[]
for i in range(0,len(xxa)):
yy=0.0
for j in range(0,self.order+1):
dy=1.0
#x[i]**j
for k in range(0,j):
dy*=xxa[i]
#a[j]*(x[i]**j)
dy*=matAResult[j]
yy+=dy
yya.append(yy)
#print(xxa,yya)
self.subfig.plot(xxa,yya,color='g',linestyle='-',marker='')
self.subfig.legend()
plt.show()
return True
except Exception as e:
print(e)
return False
#============================
# main
#============================
if __name__=="__main__":
LS = LeastSqauresCF()
#============================
#(1-1) Generate simulation data set
#============================
x = numpy.arange(-1,1,0.02)
y = [(5*a+2)*(3*a*a+1)*numpy.sin(a*2)*numpy.cos(a*4)+5 for a in x]
#============================
#(1-2) Add some noises to input and output data
#============================
x_noised=[]
y_noised=[]
i=0
for yy in y:
xx = x[i]
Ns=float(random.randint(90,110))/100
x_noised.append(xx*Ns)
y_noised.append(yy*Ns+5*Ns)
i+=1
#============================
#(1-3) Sort x, y in case x's sequence was disturbed during adding noise
#============================
zip_x_y = zip(x_noised,y_noised)
sorted_zip = sorted(zip_x_y, key=lambda x:x[0])
sorted_x, sorted_y = zip(*sorted_zip)
#print(sorted_x,sorted_y)
#============================
#(2) Processing curve fitting
#============================
if LS.ReadAnddrawInputPoints(sorted_x,sorted_y,9): #plot the orginal data curve, set order=9
MatrixFactor = LS.produceFittingCurveFactors()
LS.outputFittingCurveFunction(MatrixFactor)
LS.drawFittedCurve(matAResult=MatrixFactor)