
Jane Medium : This paper gives MicroPython Kernel Development Notes : Experimental tasks are embedded in the book Floating point arithmetic software use case in .
key word:MicroPython,MM32F3277,FFT
Software use case :
This part of the manuscript includes :
- Basic floating point arithmetic ;
- FFT operation .
- Position in manuscript :
Can be in MicroPython in Floating point number 、 The operation of complex numbers . The basic operations of floating point numbers are given below :
from math import *
a = 1.7
b = 3.4
print(a+b)
print(a*b)
print(a**b)
print(exp(a))
print(sin(b))
Operation result output :
5.1
5.78
6.074722
5.473948
-0.2555412
Function library using floating point numbers , Need to quote cmath . The following is an example of related operations on floating-point numbers :
from cmath import *
a = 1+1j
b = 0.5-1j
print(a+b)
print(a*b)
print(a**b)
print(abs(a))
print(phase(a))
exp(a)
log(b)
Output results :
(1.5+0j)
(1.5-0.5j)
(2.60549+0.1202649j)
1.414214
0.7853982
(1.468694+2.287355j)
(0.1115718-1.107149j)
By the following order , You can see math Mathematical functions that can be used in :
import math
dir(math)
The following is the command output , You can see that common mathematical functions include .
['__name__', 'pow', 'acos', 'asin', 'atan', 'atan2', 'ceil', 'copysign', 'cos', 'degrees', 'e', 'exp', 'fabs', 'floor', 'fmod', 'frexp', 'isfinite', 'isinf', 'isnan', 'ldexp', 'log', 'modf', 'pi', 'radians', 'sin', 'sqrt', 'tan', 'trunc']
stay cmath The function libraries included in are :
['__name__', 'cos', 'e', 'exp', 'log', 'phase', 'pi', 'polar', 'rect', 'sin', 'sqrt']
FFT Operation is the most commonly used algorithm in signal spectrum analysis , in the light of MicroPython Supported floating point numbers 、 Plural operation , Here is DIF( Time domain decimation fast Fourier transform ) A recursive algorithm . And the test length is 256 The Fourier transform of the hold signal .
from math import *
from cmath import *
def FFT(P):
n = len(P)
if n == 1: return P
ye = FFT(P[0::2])
yo = FFT(P[1::2])
y = [0]*n
w = exp(-1j*2*pi/n)
n2 = n//2
for j in range(n//2):
wj = w ** j
yow = [a*wj for a in yo]
y[j] = ye[j] + yow[j]
y[j+n2] = ye[j] - yow[j]
return y
LEN = 256
oneLEN = 10
p1 = [1] * oneLEN + [0] * (LEN - oneLEN)
y = FFT(p1)
yabs = [abs(yy) for yy in y]
print(yabs)
The amplitude spectrum data of Fourier transform of rectangular signal is given below . stay MM32F3277 The running time in the single chip microcomputer is 0.81 second .
[10.0, 9.97517, 9.900895, 9.777838, 9.607072, 9.390103, 9.128836, 8.825552, 8.482898, 8.103848, 7.691679, 7.249937, 6.782396, 6.293025, 5.785944, 5.265385, 4.735648, 4.201056, 3.665917, 3.134478, 2.610882, 2.099133, 1.603052, 1.126244, 0.672064, 0.2435851, 0.1564261, 0.5255356, 0.8616611, 1.163087, 1.428479, 1.656888, 1.847759, 2.000919, 2.116586, 2.195351, 2.238167, 2.246329, 2.221461, 2.165483, 2.08059, 1.96922, 1.834023, 1.677828, 1.503605, 1.314431, 1.113455, 0.9038545, 0.6888052, 0.4714402, 0.2548177, 0.04188573, 0.1645496, 0.3618536, 0.5475908, 0.7195493, 0.8757596, 1.014518, 1.134397, 1.234257, 1.313254, 1.370846, 1.406789, 1.421134, 1.414214, 1.386666, 1.339365, 1.273443, 1.190256, 1.09137, 0.9785301, 0.8536346, 0.7187103, 0.5758811, 0.4273379, 0.2753101, 0.1220333, 0.03027992, 0.1794671, 0.3234483, 0.460248, 0.5880249, 0.7050903, 0.8099316, 0.9012283, 0.9778691, 1.038963, 1.083848, 1.1121, 1.12353, 1.11819, 1.096367, 1.058574, 1.005545, 0.9382177, 0.8577236, 0.7653668, 0.6626039, 0.5510257, 0.432332, 0.3083075, 0.1807963, 0.05167642, 0.07716717, 0.2038682, 0.3266045, 0.4436239, 0.5532675, 0.6539917, 0.7443892, 0.8232089, 0.8893699, 0.9419779, 0.9803374, 1.003956, 1.012556, 1.006073, 0.9846593, 0.9486776, 0.898699, 0.8354924, 0.760011, 0.6733827, 0.576894, 0.4719654, 0.3601391, 0.2430533, 0.1224208, 0.0, 0.1224198, 0.2430533, 0.3601391, 0.4719653, 0.5768936, 0.6733835, 0.7600111, 0.8354924, 0.8986997, 0.9486781, 0.9846594, 1.006073, 1.012556, 1.003957, 0.9803378, 0.9419788, 0.8893703, 0.823209, 0.7443897, 0.653992, 0.5532677, 0.4436243, 0.3266048, 0.2038684, 0.07716741, 0.05167619, 0.1807961, 0.3083073, 0.4323315, 0.551025, 0.6626033, 0.7653668, 0.8577241, 0.9382182, 1.005545, 1.058574, 1.096366, 1.118189, 1.123529, 1.112099, 1.083847, 1.038961, 0.9778674, 0.9012262, 0.8099288, 0.7050877, 0.5880218, 0.4602449, 0.3234443, 0.1794629, 0.03027497, 0.1220383, 0.2753156, 0.4273441, 0.5758879, 0.7187173, 0.8536419, 0.9785377, 1.091378, 1.190264, 1.273451, 1.339374, 1.386675, 1.414214, 1.421124, 1.406779, 1.370837, 1.313245, 1.234248, 1.134388, 1.014509, 0.8757509, 0.7195406, 0.5475829, 0.3618463, 0.1645427, 0.04189257, 0.2548237, 0.4714459, 0.6888097, 0.9038591, 1.113459, 1.314435, 1.503608, 1.677831, 1.834026, 1.969222, 2.080592, 2.165484, 2.221462, 2.24633, 2.238166, 2.19535, 2.116585, 2.000918, 1.847759, 1.65689, 1.42848, 1.163088, 0.8616615, 0.5255361, 0.1564267, 0.2435843, 0.6720631, 1.126243, 1.603051, 2.099132, 2.610881, 3.134475, 3.665913, 4.201052, 4.735641, 5.265379, 5.785938, 6.293019, 6.78239, 7.24993, 7.691671, 8.103838, 8.482887, 8.825541, 9.128823, 9.390092, 9.607058, 9.777821, 9.900881, 9.975152]
>>>
The following is the spectrum waveform drawn from the amplitude spectrum , It can verify the correctness of the calculated data . Through the test, we can know , At present MM32F3277 Medium MicroPython The maximum supported length is 256 Of FFT. exceed 256 length , The memory of single-chip microcomputer is insufficient .
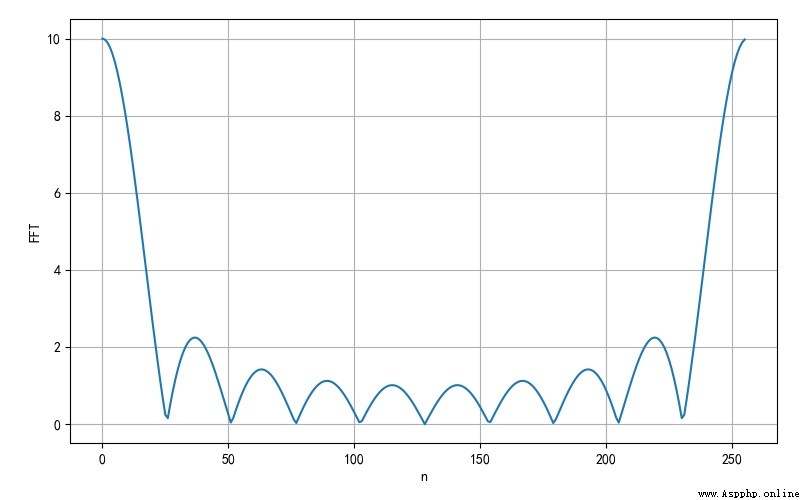
▲ 256 The length of the rectangular signal corresponds to FFT Amplitude spectrum of results
This paper gives MicroPython Kernel Development Notes : Experimental tasks are embedded in the book Floating point arithmetic software use case in .
■ Links to related literature :
● Related chart Links :