二叉搜索樹相關題目總結（二） 力扣 Python

前文 二叉搜索樹相關題目總結（一） 中，主要是涉及二叉搜索樹中的一些操作。

這篇文章是列舉兩道與構造 BST 有關的題目。

96. 不同的二叉搜索樹

解題思路：

給定一個 n， 問從 1 到 n 能組成互不相同的 BST 有幾種？

簡單來看，就是窮舉所有可能的樹，然後算一下結果。

第一種方法，遞歸 DFS, 也是回溯的一種體現。

加入了名為 cache 的數組，也就是 dp 數組用於消除子問題重疊。

class Solution:
def numTrees(self, n: int) -> int:
cache = [-1] * (n + 1) # 初始化數組長度
return self.countTrees(n, cache)
def countTrees(self,n, cache):
#兩個 base case
if n == 0:
return 1
if n == 1:
return 1
# -1 是數組初始化的值，只要不是 -1 就是已經存在的子問題，直接返回
if cache[n] != -1:
return cache[n]
#記錄總的個數
res = 0
for i in range(n):
#分別列舉可能構成的左右子樹個數
LeftTrees = self.countTrees(i, cache)
RightTrees = self.countTrees(n - i - 1, cache)
#以 i 為節點的樹，其能構成不同的 BST 數目為 左右子樹的乘機
res += LeftTrees * RightTrees
#從下往上記錄節點組成樹的個數
cache[n] = res
return res

解法二：

其實和解法一一致，只不過引入了 lru_cache 包，可以理解為一個隱式 cache 裝飾器，用於自動緩存子問題。

代碼相對於簡潔。

class Solution:
def numTrees(self, n: int) -> int:
return self.countTrees(n)
@lru_cache
def countTrees(self, n: int) -> int:
if n == 0:
return 1
if n == 1:
return 1
res = 0
for i in range(n):
left = self.countTrees(i)
right = self.countTrees(n - i - 1)
res += left * right
return res

解法三：

動態規劃，動態規劃不明白可以看一下官方解釋的圖。

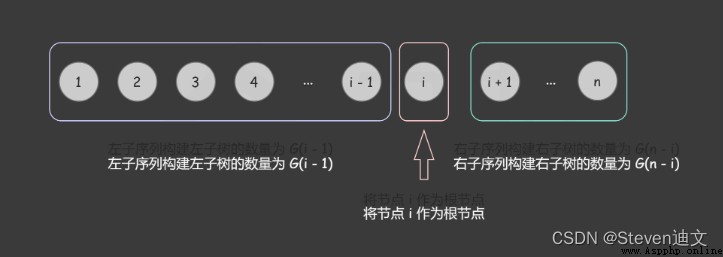
動態規劃是一種從底向上的 DFS。

dp 數組用於記錄重復子問題。

class Solution:
def numTrees(self, n: int) -> int:
#初始化 dp 數組
dp = [0] * (n + 1)
dp[0], dp[1] = 1, 1
for i in range(2, n + 1):
for j in range(i):
#動態轉移方程，窮舉子問題
dp[i] += dp[j] * dp[i - j - 1]
return dp[n]

95. 不同的二叉搜索樹 II

解題思路：
與 一思路一致，但這次要具體列出可能的子樹，直接使用 DFS 然後記錄每次可能的子樹。

# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def generateTrees(self, n: int) -> List[TreeNode]:
if n == 0:
return []
return self.helper(1, n)
def helper(self, start, end):
if start > end:
return[None]
#記錄所有可能的二叉搜索樹
res = []
#對每一個數值窮舉
for curRoot in range(start , end + 1):
#遞歸生成可能的左右子樹
leftSubtrees = self.helper(start, curRoot - 1)
rightSubtrees = self.helper(curRoot + 1, end)
for leftTree in leftSubtrees:
for rightTree in rightSubtrees:
#合並每一個可能的組合
root = TreeNode(curRoot)
root.left = leftTree
root.right = rightTree
#添加組合
res.append(root)
return res