Summary of related topics of binary search tree (I) force deduction Python

Summarize the problems related to binary search tree , The solution is the related operation of binary search tree .

98. Verify binary search tree

Their thinking ：

Verify whether a tree is a binary search tree （BST）？

Write code according to the nature of binary search tree , Note as follows .

# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isValidBST(self, root: Optional[TreeNode]) -> bool:
return self.check(root)
def check(self, root, min_val = float('-inf'), max_val = float('inf')) -> bool:
# The default is True
if not root:
return True
# Once the current node is smaller than the minimum , Or greater than the maximum , It's not a binary search tree 
if root.val <= min_val or root.val >= max_val:
return False
# Check the left subtree and right subtree respectively 
return self.check(root.left, min_val, root.val) and self.check(root.right, root.val, max_val)

700. Search in binary search tree

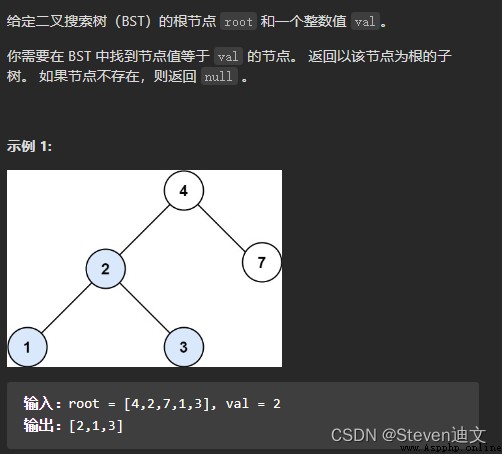
Their thinking ：
utilize BST Characteristics of , To search .

If the current node is less than the target value, go to the right subtree to find .

If the current node is larger than the target value, go to the left subtree to find .

# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def searchBST(self, root: TreeNode, val: int) -> TreeNode:
if not root:
return None
# Using the properties of binary search tree , lookup val
if val < root.val:
return self.searchBST(root.left, val)
if val > root.val:
return self.searchBST(root.right, val)
return root

701. Insert operation in binary search tree

Their thinking ：

On the basis of binary search tree search , Modify the relevant code variation insert .

# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def insertIntoBST(self, root: TreeNode, val: int) -> TreeNode:
# Find an empty location to insert a new node 
if not root:
return TreeNode(val)
# Receive the return value of recursive call 
if val < root.val:
root.left = self.insertIntoBST(root.left, val)
if val > root.val:
root.right = self.insertIntoBST(root.right, val)
return root

450. Delete nodes in binary search tree

Their thinking ：

BST The deletion of is more complicated than the previous three questions .

There are mainly three cases of deleted nodes in the tree .

• situation 1, The current node has no children , Delete directly .
• situation 2, The current node has a left child node or a right child node , Delete the current node , And replace the current child node with the existing child node .
• situation 3, The right two child nodes of the current node , Delete the current node , Replace with the of the largest node in the left child node , Or use the smallest of the right child nodes to replace .

# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def deleteNode(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:
if not root:
return None
if root.val > key:
root.left = self.deleteNode(root.left, key)
elif root.val < key:
root.right = self.deleteNode(root.right, key)
# Found node value is key
else:
# Deal with the situation 1, 2
if not root.left:
return root.right
if not root.right:
return root.left
# Deal with the situation 3, Here, the smallest of the right subtrees is used to replace 
minNode = self.getMin(root.right)
# Delete the smallest node in the right subtree 
root.right = self.deleteNode(root.right, minNode.val)
# Replacement node 
minNode.left, minNode.right = root.left, root.right
root = minNode
return root
def getMin(self, root):
# according to BST The nature of , The one on the far left is the smallest 
while root.left:
root = root.left
return root