Summary of related topics of binary search tree (II) force deduction Python

above Binary search tree related topics summary （ One ） in , It mainly involves some operations in the binary search tree .

This article is to enumerate two ways and structures BST Related topics .

96. Different binary search trees

Their thinking ：

Given a n, Ask from 1 To n Can form different BST There are several kinds of ？

Simple view , Is to enumerate all possible trees , Then calculate the result .

The first method , recursive DFS, It is also a reflection of backtracking .

Joined a group called cache Array of , That is to say dp Array is used to eliminate the overlap of sub problems .

class Solution:
def numTrees(self, n: int) -> int:
cache = [-1] * (n + 1) # Initialize array length 
return self.countTrees(n, cache)
def countTrees(self,n, cache):
# Two base case
if n == 0:
return 1
if n == 1:
return 1
# -1 Is the value of array initialization , As long as it's not -1 Is the sub problem that already exists , Go straight back to 
if cache[n] != -1:
return cache[n]
# Record the total number 
res = 0
for i in range(n):
# List the number of possible left and right subtrees 
LeftTrees = self.countTrees(i, cache)
RightTrees = self.countTrees(n - i - 1, cache)
# With i Tree for nodes , It can make up different BST The number is The opportunity of the left and right subtrees 
res += LeftTrees * RightTrees
# Record the number of node composition trees from bottom to top 
cache[n] = res
return res

Solution 2 ：

In fact, it is consistent with the solution , Just introduced lru_cache package , It can be understood as an implicit cache Decorator , Used to automatically cache sub problems .

The code is relatively simple .

class Solution:
def numTrees(self, n: int) -> int:
return self.countTrees(n)
@lru_cache
def countTrees(self, n: int) -> int:
if n == 0:
return 1
if n == 1:
return 1
res = 0
for i in range(n):
left = self.countTrees(i)
right = self.countTrees(n - i - 1)
res += left * right
return res

Solution 3 ：

Dynamic programming , If you don't understand dynamic planning, you can take a look at the official explanation .

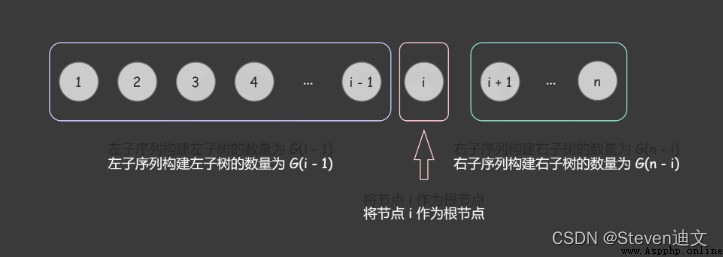
Dynamic programming is a bottom-up approach DFS.

dp The array is used to record repeated sub problems .

class Solution:
def numTrees(self, n: int) -> int:
# initialization dp Array 
dp = [0] * (n + 1)
dp[0], dp[1] = 1, 1
for i in range(2, n + 1):
for j in range(i):
# Dynamic transfer equation , Exhaustive subproblem 
dp[i] += dp[j] * dp[i - j - 1]
return dp[n]

95. Different binary search trees II

Their thinking ：
And The same idea , But this time we need to list the possible subtrees , Use it directly DFS Then record every possible subtree .

# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def generateTrees(self, n: int) -> List[TreeNode]:
if n == 0:
return []
return self.helper(1, n)
def helper(self, start, end):
if start > end:
return[None]
# Record all possible binary search trees 
res = []
# For each value, enumerate 
for curRoot in range(start , end + 1):
# Recursively generate possible left and right subtrees 
leftSubtrees = self.helper(start, curRoot - 1)
rightSubtrees = self.helper(curRoot + 1, end)
for leftTree in leftSubtrees:
for rightTree in rightSubtrees:
# Merge every possible combination 
root = TreeNode(curRoot)
root.left = leftTree
root.right = rightTree
# Add combination 
res.append(root)
return res