Enumeration method of Python for solving mathematical problems

As a student of grade two , Math problems are always troubling me . Especially the preparatory examination here （ That is, the two best high schools here recruit students one year in advance , An examination to select top students ） nearly , The math problems I'm facing are getting more and more painful .

see , Trouble is coming. ：

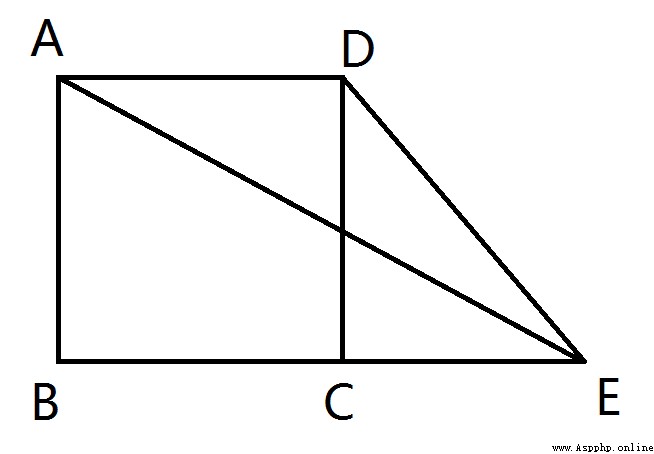
Pictured , In the square ABCD in ,E In the ray BC On , Connect AE、CE, be DE/AE The minimum value of is ________.

Get this question , Confidence slowly I calmly set AB:CE by 1:x, namely AB=k,CE=xk, So the original formula （ Set to y）=[k^2+(xk)^2]^0.5/[k^2+(k+xk)^2]^0.5（ there “^” On behalf of the power ）. That's all we need [k^2+(xk)^2]/[k^2+(k+xk)^2] The minimum value of ！ This is a problem of finding the minimum value of an algebraic formula .

But …… The more you look at it, the more wrong it is . This algebraic expression is a fraction , However, the same type of questions we often contact are only integral forms . With my impression of six junior high school math books , I can't help asking questions ： Is this really the content of junior high school ？ There seems to be no mention in the book ？

however , In the spirit of hard-working old scalper , I spent hours there with this topic fruitlessly . Final , I gave up .

But maybe it's inspiration from a dream , The next morning , It occurred to me that ： Why not pass a Python Program to enumerate one by one , Choose an approximate value from them ？

therefore , The first program came out ：

k=1
answer=100
myx=0
for x in range(10):
y=(k**2+(x*k)**2)**0.5/(k**2+(k+x*k)**2)**0.5
if y<answer:
answer=y
myx=x
print(answer,myx)

Output results ：

0.6324555320336759 1

alas , The more you look at it, the more something goes wrong ？

Last , I finally found the problem ： Traverse like this x, Its values are all integers , In fact, the smallest y The corresponding x It doesn't have to be an integer .

Good. , Let's change ：

k=1
answer=100
myx=0
for x in range(10000):
x=x/1000
y=(k**2+(x*k)**2)**0.5/(k**2+(k+x*k)**2)**0.5
if y<answer:
answer=y
myx=x
print(answer,myx)

Output ：

0.6180339889095493 0.618

There's no problem with this ？ There is still a problem . How can you be sure of x The range of ？

This problem seems fatal , But it's not completely incomprehensible . We can roughly infer that ,y The change trend of should be first down and then up or first up and then down （ This reasoning is instinctive to me , So that I can't explain the process in detail , But it can be concluded by reasoning ）, Since it is to find the minimum , Of course, it is the former . therefore , because x from o.618 To 1 Is increasing , therefore x It must be 0.618 Or below , And these numbers obviously we have traversed to （ At least in a certain precision ）. Next , All we need is to improve the accuracy , So as to get a result closer to the real value , And use it to guess the right answer .

Final , With high accuracy （ The procedure is roughly the same as before , Just increase the traversal value and x A multiple of reduction , Not listed here ）, We get the results ：

0.6180339887498948 0.618034

We all know , Before the decimal point of the golden ratio 65 Bit is equal to 0.6180339887498948482045868343656381177203091798057628621354486227, The first few digits of this number are completely consistent with the result of our traversal . We have reason to believe that , The answer is the golden ratio (5^0.5-1)/2. therefore , We use it perfectly Python That solved the problem .

Of course , Later, our teacher explained to us how to solve this problem without procedures ： Try to change the unknown part of the formula into x+a/x In the form of , This formula will never be less than 2a^0.5. such , We can get the maximum value .