1、 Why do I need to choose an independent variable ?
2、 Several criteria for the selection of independent variables
(1) The degree of freedom adjusts the complex determination coefficient to the maximum
(2) Akaike info criterion AIC To achieve the minimum
3、 All subset regression
(1) Algorithmic thought
(2) Data set situation
(3) Code section
(4) Output results
4、 backward
(1) Algorithmic thought
(2) Data set situation
(3) Code section
(4) Result display
5、 Stepwise regression
(1) Algorithmic thought
(2) Data set situation
(3) Code section
(4) Result display
1、 Why do I need to choose an independent variable ?A good regression model , Not the number of independent variables, the more the better . When building the regression model , The basic guiding ideology of selecting independent variables is less but better . Some pairs of dependent variables are discarded y After the influential independent variable , The price paid is that the estimator is biased , But the variance of the prediction bias will decrease . therefore , The choice of independent variables has important practical significance .
2、 Several criteria for the selection of independent variables (1) The degree of freedom adjusts the complex determination coefficient to the maximum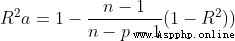

So called all subset regression , Is to consider all subsets of the total independent variable , See which subset is the best solution .
(2) Data set situation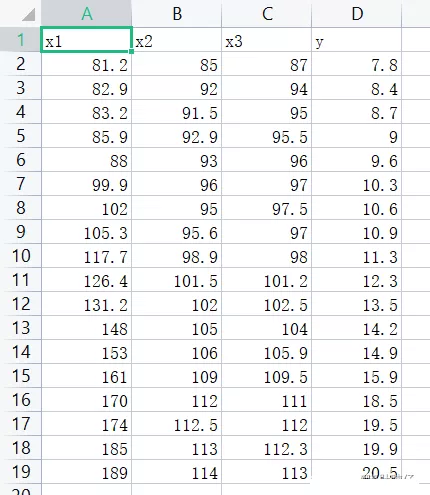
import pandas as pdimport numpy as npimport statsmodels.api as smimport statsmodels.formula.api as smffrom itertools import combinationsdef allziji(df): list1 = [1,2,3] n = 18 R2 = [] names = [] # Find all subsets , And cycle in turn for a in range(len(list1)+1): for b in combinations(list1,a+1): p = len(list(b)) data1 = pd.concat([df.iloc[:,i-1] for i in list(b) ],axis = 1)# Combine the required factors name = "y~"+("+".join(data1.columns))# Composition formula data = pd.concat([df['y'],data1],axis=1)# Combine independent and dependent variables result = smf.ols(name,data=data).fit()# modeling # Calculation R2a r2 = (n-1)/(n-p-1) r2 = r2 * (1-result.rsquared**2) r2 = 1 - r2 R2.append(r2) names.append(name) finall = {" The formula ":names, "R2a":R2} data = pd.DataFrame(finall) print(""" According to the criterion of adjusting the complex determination coefficient of degrees of freedom, we get : The optimal subset regression model is :{}; Its R2a The value is :{}""".format(data.iloc[data['R2a'].argmax(),0],data.iloc[data['R2a'].argmax(),1])) result = smf.ols(name,data=df).fit()# modeling print() print(result.summary())df = pd.read_csv("data5.csv")allziji(df)(4) Output results 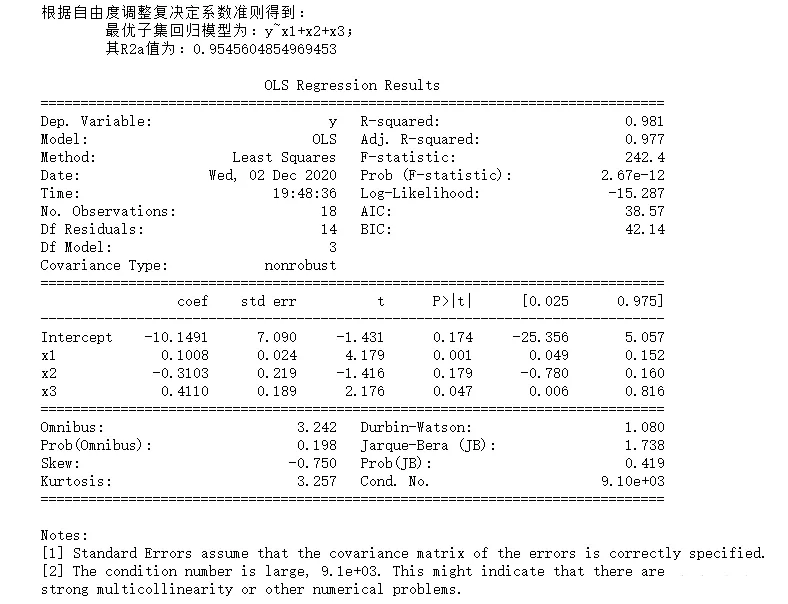
The backward method is the opposite of the forward method , Usually start with all m Establish a regression equation with three variables , Then calculate the corresponding of the regression equation after eliminating any variable AIC The value of the statistic , Choose the smallest AIC The variable corresponding to the value that needs to be eliminated , Remember x1; then , Establish and eliminate variables x1 The subsequent dependent variable y On surplus m-1 Regression equation of variables , Calculate the value of the regression equation after removing any variable from the regression equation AIC value , Choose the smallest AIC Value and determine the variables that should be eliminated ; And so on , Until the remaining in the regression equation p Remove any one of the variables AIC The value will increase , At this time, there are no independent variables that can be eliminated , So include this p The regression equation of variables is the final equation .
(2) Data set situation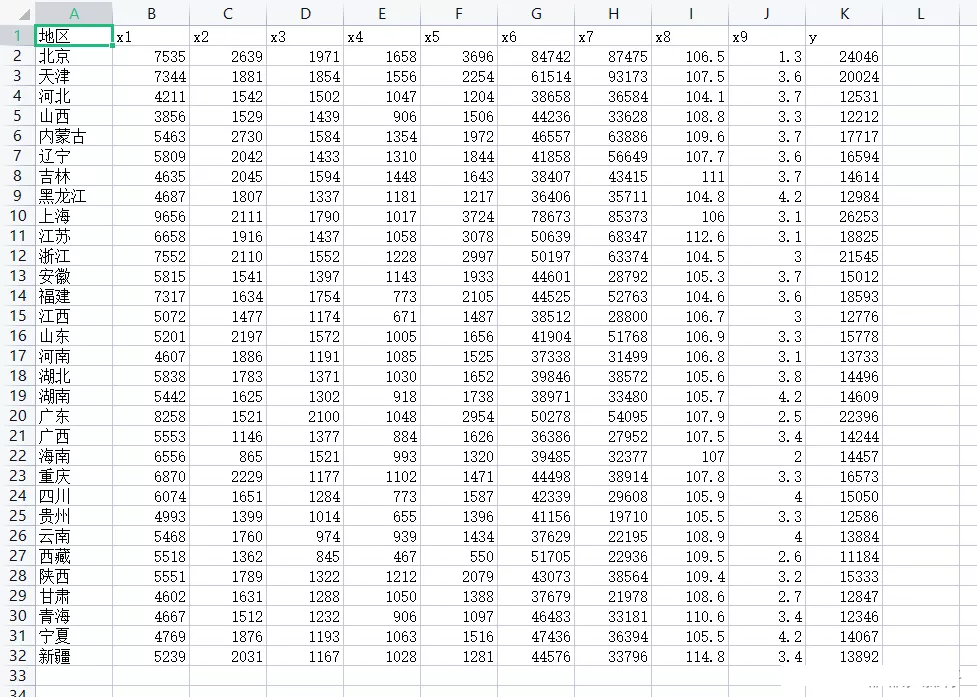
import pandas as pdimport numpy as npimport statsmodels.api as smimport statsmodels.formula.api as smfdef backward(df): all_bianliang = [i for i in range(0,9)]# Standby factor ceshi = [i for i in range(0,9)]# Store the model after adding a single factor zhengshi = [i for i in range(0,9)]# Collect determining factors data1 = pd.concat([df.iloc[:,i+1] for i in ceshi ],axis = 1)# Combine the required factors name = 'y~'+'+'.join(data1.columns) result = smf.ols(name,data=df).fit()# modeling c0 = result.aic # Minimum aic delete = []# Deleted element while(all_bianliang): aic = []# Deposit aic for i in all_bianliang: ceshi = [i for i in zhengshi] ceshi.remove(i) data1 = pd.concat([df.iloc[:,i+1] for i in ceshi ],axis = 1)# Combine the required factors name = "y~"+("+".join(data1.columns))# Composition formula data = pd.concat([df['y'],data1],axis=1)# Combine independent and dependent variables result = smf.ols(name,data=data).fit()# modeling aic.append(result.aic)# Will all aic Deposit in if min(aic)>c0:#aic Has reached the minimum data1 = pd.concat([df.iloc[:,i+1] for i in zhengshi ],axis = 1)# Combine the required factors name = "y~"+("+".join(data1.columns))# Composition formula break else: zhengshi.remove(all_bianliang[aic.index(min(aic))])# Find the smallest aic And put the smallest factor into the formal model list c0 = min(aic) delete.append(aic.index(min(aic))) all_bianliang.remove(all_bianliang[delete[-1]])# Delete deleted factor name = "y~"+("+".join(data1.columns))# Composition formula print(" The optimal model is :{}, Its aic by :{}".format(name,c0)) result = smf.ols(name,data=df).fit()# modeling print() print(result.summary())df = pd.read_csv("data3.1.csv",encoding='gbk')backward(df)(4) Result display 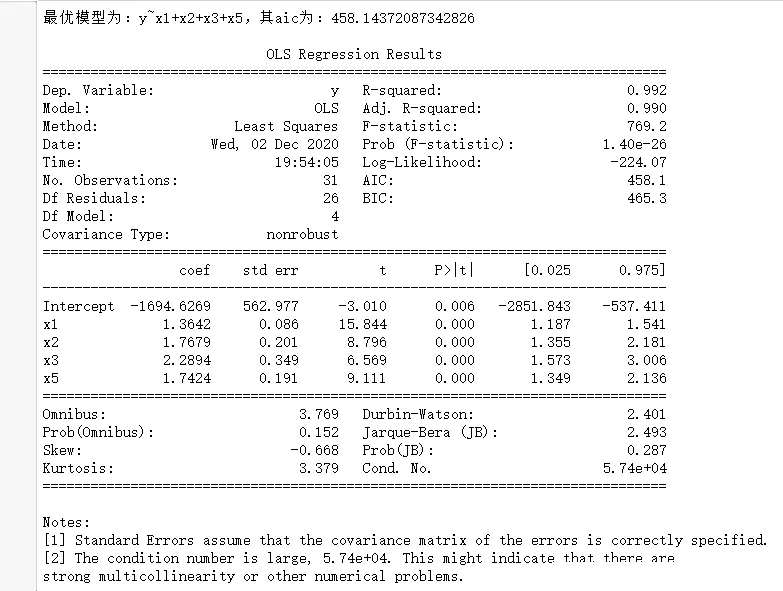
The basic idea of stepwise regression is to go in and out .R In language step() The specific method of the function is to include p After the initial model of variables , Calculate the of the initial model AIC value , On the basis of this model p Add variables and the rest m-p After any of the variables AIC value , Then choose the smallest AIC Determine whether the new value of the added variable in the model exists or not . So repeatedly , Until no new variables are added and no existing variables in the model are eliminated AIC Minimum value , You can stop the calculation , And return the final result .
(2) Data set situation
import pandas as pdimport numpy as npimport statsmodels.api as smimport statsmodels.formula.api as smfdef zhubuhuigui(df): forward = [i for i in range(0,4)]# Alternative factors backward = []# Standby factor ceshi = []# Store the model after adding a single factor zhengshi = []# Collect determining factors delete = []# Deleted factor while forward: forward_aic = []# Forward aic backward_aic = []# back off aic for i in forward: ceshi = [j for j in zhengshi] ceshi.append(i) data1 = pd.concat([df.iloc[:,i] for i in ceshi ],axis = 1)# Combine the required factors name = "y~"+("+".join(data1.columns))# Composition formula data = pd.concat([df['y'],data1],axis=1)# Combine independent and dependent variables result = smf.ols(name,data=data).fit()# modeling forward_aic.append(result.aic)# Will all aic Deposit in for i in backward: if (len(backward)==1): pass else: ceshi = [j for j in zhengshi] ceshi.remove(i) data1 = pd.concat([df.iloc[:,i] for i in ceshi ],axis = 1)# Combine the required factors name = "y~"+("+".join(data1.columns))# Composition formula data = pd.concat([df['y'],data1],axis=1)# Combine independent and dependent variables result = smf.ols(name,data=data).fit()# modeling backward_aic.append(result.aic)# Will all aic Deposit in if backward_aic: if forward_aic: c0 = min(min(backward_aic),min(forward_aic)) else: c0 = min(backward_aic) else: c0 = min(forward_aic) if c0 in backward_aic: zhengshi.remove(backward[backward_aic.index(c0)]) delete.append(backward_aic.index(c0)) backward.remove(backward[delete[-1]])# Delete deleted factor forward.append(backward[delete[-1]]) else: zhengshi.append(forward[forward_aic.index(c0)])# Find the smallest aic And put the smallest factor into the formal model list forward.remove(zhengshi[-1])# Delete existing factors backward.append(zhengshi[-1]) name = "y~"+("+".join(data1.columns))# Composition formula print(" The optimal model is :{}, Its aic by :{}".format(name,c0)) result = smf.ols(name,data=data).fit()# modeling print() print(result.summary())df = pd.read_csv("data5.5.csv",encoding='gbk')zhubuhuigui(df)(4) Result display 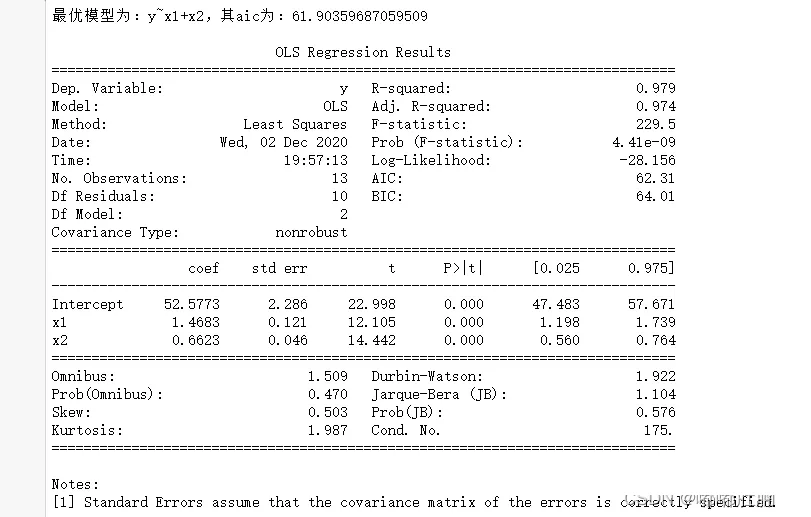
This is about python Selection of arguments for ( All subset regression , backward , Stepwise regression ) This is the end of the article , More about python Please search the previous articles of SDN or continue to browse the related articles below. I hope you will support SDN more in the future !