One 、 Subject requirements ：

Content ：

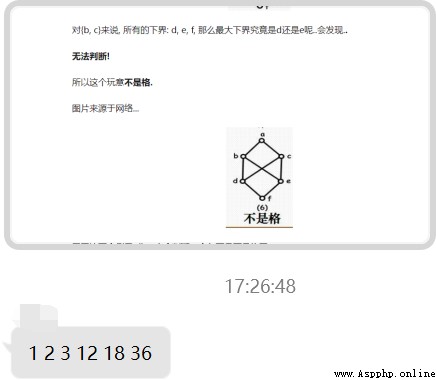
         Find the set A On the division relationship R The corresponding covering relation , And determine the poset <A,R> Whether it is a case , If case , Judge whether it is a complemented lattice .

requirement ：

         aggregate A It can be any set of positive integers given by the user .

Two 、 Experiment principle and content ：

The data structure used in the experiment 、 Storage structure ： List and its sort Sort , Yuan Zu (a,b) Express a|b(a to be divisible by b) as well as map mapping

The function in the experiment ：

def judge_div(a,b)  # Judge the divisible relation 1、0 Indicates whether the integer division relationship is satisfied

def judge_COV(A) # Incoming collection A, First, judge what is consistent with the relationship of division R aggregate , Then judge the covering relationship , Returns the covering relationship in the form of a list （ One call judge_div(a,b) Function to determine R aggregate ）

def union(a,b,A) #A Collection a、b The union of elements ( Get the supremum of the two )

def intersect(a,b,A) #A Collection a,b Intersection of elements ( Get the infimum of both ), One call judge_div(a,b) Function traverses down A The elements in , Find the minimum lower bound （ There is , Returns the supremum and infimum , There is no return 0）

def judge_lattice(A) # Judge whether it is a lattice and whether it is a complement lattice , According to the definition of lattice , call union and intersect Function to judge .
def print_tuple(R) # Format output set

Data transfer relationship in the experiment ： Input set A, The element must be a collection of positive integers , Commas separate adjacent elements , Call a series of functions to process

Experimental ideas and principles ：

• To judge whether or not the relation of integral division is true R Set and cover relationships ： Go through one by one A Each element in , call judge_div Function to determine whether it conforms to the integer division relationship , yes -> Put it in the form of Yuanzu R in .R After calculation , Right again R Every order pair in （ Yuan Zu ） Judge : stay R Collection , And there is no third party to traverse one by one , Once it appears <x,y><y,z>,flag=0, Exit loop , if flag After traversal, it is still 1, Put in COVA In the ordered couple of .
• Judgement lattice ： By definition ( Any two elements will have supremum and infimum ), call union and intersect Function to find the supremum and infimum （ There is , Returns the supremum and infimum , There is no return 0）
• Judge that there is a complement ： Under the premise of case , For each element, traverse one by one to find A The element in can be its complement ( Supremum after union operation 1 The infimum after the sum intersection operation 0) that will do ,（ As long as you find a complement, you can quit the discussion of that element , When only A Each element in the has at least one complement , At this time, it can be judged as a complemented lattice -> Once you traverse to an element that cannot find a complement , Exit the loop directly ,flag2=0, It's not a supplement ）

Time complexity ：O（n²）

3、 ... and 、 Source code ：

# Cover the relationship to get a pass .py
def judge_div(a,b):
'''a to be divisible by b->b Divide a Integers '''
max=(a if a>b else b)
min=a+b-max
if max%min==0:# to be divisible by
return 1
else:
return 0
def judge_COV(A):# Incoming collection A, To judge whether or not the relation of integral division is true R aggregate , Then judge the covering relationship
R=[]# Storage R aggregate
for i in A:
for j in A[A.index(i):]:
if judge_div(i,j):
R.append(tuple([i,j]))
# obtain R The set of relationships , Lower request COV A
COVA=[]
for x in R:
if x[1]-x[0]==1:
COVA.append(x)
elif (x[1]-x[0])>1: # Be careful to exclude reflexive <1,1> Equal elements
flag=1 # The assumption is consistent with
template=A[A.index(x[0])+1:A.index(x[1])]
for y in template:
if R.count(tuple([x[0],y]))==1 and R.count(tuple([y,x[1]]))==1: # There is no other element in the middle to satisfy the covering relationship
flag=0
break
if flag==1:
COVA.append(x)
return COVA
''' Format output poset '''
def print_tuple(R):
print("{",end="")
for i in R:
print("<{0},{1}>".format(i[0],i[1]),end="")
print("}")
''' The union of two elements -> Get the supremum of the two elements '''
def union(a,b,A):
max=(a if a>b else b)
for i in A[A.index(max):]:
if judge_div(i,a) ==1 and judge_div(i,b)==1:
return i
return 0# if 0 Express A Medium a,b The supremum of the element is not A in
''' The intersection of two elements -> Get the infimum of two elements '''
def intersect(a,b,A):
min=(a if a<b else b)
for i in A[A.index(min)::-1]:
if judge_div(b,i)==1 and judge_div(a,i)==1:
return i
return 0
''' Judge whether it is a lattice and whether it is a complement lattice '''
def judge_lattice(A):
# Let's make a case related judgment ( Any two elements have their supremum and infimum )
flag1=1# grid
flag2=1
f=1
for x in A:
if flag1==0:
break
else:
for y in A[A.index(x)+1:]:
flag1=bool(union(x,y,A) and intersect(x,y,A))# Be careful and The return value of ！！！！
if flag1==0:
break
for m in A:
if f==1:
f=0
for n in A:
if intersect(m,n,A)==A[0] and union(m,n,A)==A[-1]:
f=1
break
else:
flag2=0
if flag1==0:
print("<A,|> Not a grid ")
elif flag2==0:
print("<A,|> It's a lattice , But there is no complement ")
else:
print("<A,|> It's a lattice , And it is a complemented lattice ")
if __name__=="__main__":
# Input set A, aggregate A It can be any set of positive integers given by the user .
tempstr=input(" Input set A, The element must be a collection of positive integers , Commas separate adjacent elements ")
Alist=tempstr.split(",")
A=list(map(int,Alist))
A.sort(reverse=False)# Ascending sort for example ：1 2 4 8 etc.
COVA=judge_COV(A)
print("A The corresponding covering relation is :",end="")
print_tuple(COVA)
judge_lattice(A)

2022.6.29 At the end ,

One example does not consider , Readers can modify , This example is shown below .