1、為什麼需要自變量選擇？
2、自變量選擇的幾個准則
（1）自由度調整復決定系數達到最大
（2）赤池信息量AIC達到最小
3、所有子集回歸
（1）算法思想
（2）數據集情況
（3）代碼部分
（4）輸出結果
4、後退法
（1）算法思想
（2）數據集情況
（3）代碼部分
（4）結果展示
5、逐步回歸
（1）算法思想
（2）數據集情況
（3）代碼部分
（4）結果展示
1、為什麼需要自變量選擇？一個好的回歸模型，不是自變量個數越多越好。在建立回歸模型的時候，選擇自變量的基本指導思想是少而精。丟棄了一些對因變量y有影響的自變量後，所付出的代價就是估計量產生了有偏性，但是預測偏差的方差會下降。因此，自變量的選擇有重要的實際意義。
2、自變量選擇的幾個准則（1）自由度調整復決定系數達到最大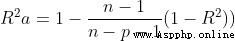
所謂所有子集回歸，就是將總的自變量的所有子集進行考慮，查看哪一個子集是最優解。
（2）數據集情況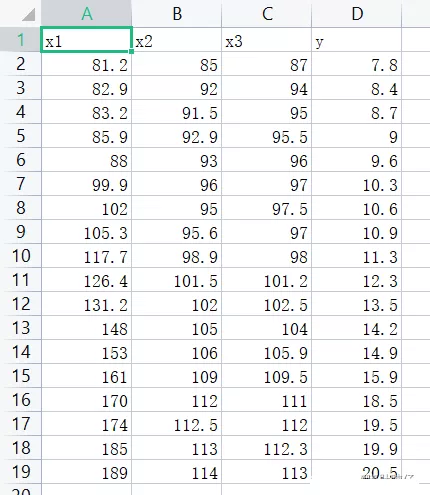
import pandas as pdimport numpy as npimport statsmodels.api as smimport statsmodels.formula.api as smffrom itertools import combinationsdef allziji(df): list1 = [1,2,3] n = 18 R2 = [] names = [] #找到所有子集，並依次循環 for a in range(len(list1)+1): for b in combinations(list1,a+1): p = len(list(b)) data1 = pd.concat([df.iloc[:,i-1] for i in list(b) ],axis = 1)#結合所需因子 name = "y~"+("+".join(data1.columns))#組成公式 data = pd.concat([df['y'],data1],axis=1)#結合自變量和因變量 result = smf.ols(name,data=data).fit()#建模 #計算R2a r2 = (n-1)/(n-p-1) r2 = r2 * (1-result.rsquared**2) r2 = 1 - r2 R2.append(r2) names.append(name) finall = {"公式":names, "R2a":R2} data = pd.DataFrame(finall) print("""根據自由度調整復決定系數准則得到： 最優子集回歸模型為：{}； 其R2a值為：{}""".format(data.iloc[data['R2a'].argmax(),0],data.iloc[data['R2a'].argmax(),1])) result = smf.ols(name,data=df).fit()#建模 print() print(result.summary())df = pd.read_csv("data5.csv")allziji(df)（4）輸出結果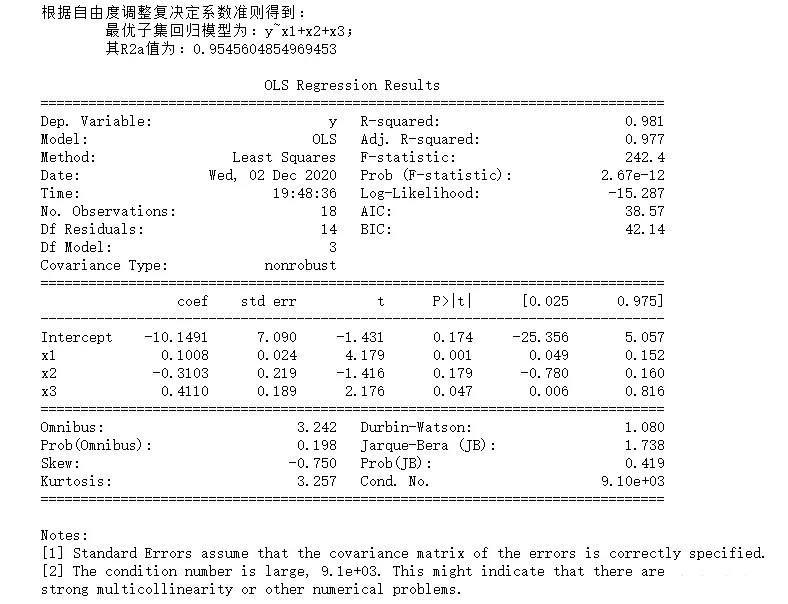
後退法與前進法相反，通常先用全部m個變量建立一個回歸方程，然後計算在剔除任意一個變量後回歸方程所對應的AIC統計量的值，選出最小的AIC值所對應的需要剔除的變量，不妨記作x1;然後，建立剔除變量x1後因變量y對剩余m-1個變量的回歸方程，計算在該回歸方程中再任意剔除一個變量後所得回歸方程的AIC值，選出最小的AIC值並確定應該剔除的變量;依此類推，直至回歸方程中剩余的p個變量中再任意剔除一個 AIC值都會增加，此時已經沒有可以繼續剔除的自變量，因此包含這p個變量的回歸方程就是最終確定的方程。
（2）數據集情況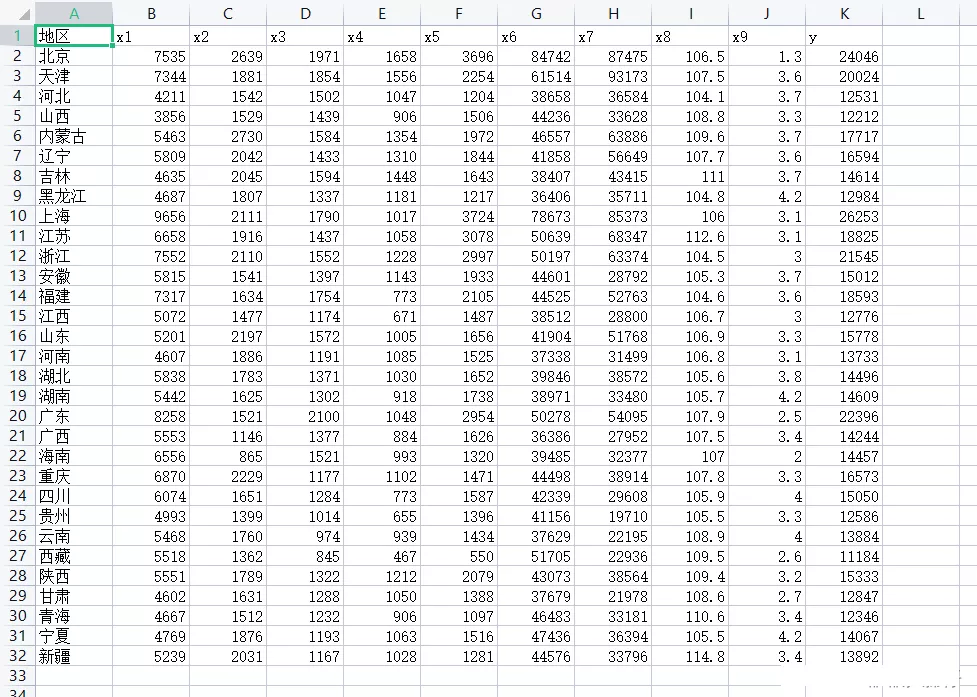
import pandas as pdimport numpy as npimport statsmodels.api as smimport statsmodels.formula.api as smfdef backward(df): all_bianliang = [i for i in range(0,9)]#備退因子 ceshi = [i for i in range(0,9)]#存放加入單個因子後的模型 zhengshi = [i for i in range(0,9)]#收集確定因子 data1 = pd.concat([df.iloc[:,i+1] for i in ceshi ],axis = 1)#結合所需因子 name = 'y~'+'+'.join(data1.columns) result = smf.ols(name,data=df).fit()#建模 c0 = result.aic #最小aic delete = []#已刪元素 while(all_bianliang): aic = []#存放aic for i in all_bianliang: ceshi = [i for i in zhengshi] ceshi.remove(i) data1 = pd.concat([df.iloc[:,i+1] for i in ceshi ],axis = 1)#結合所需因子 name = "y~"+("+".join(data1.columns))#組成公式 data = pd.concat([df['y'],data1],axis=1)#結合自變量和因變量 result = smf.ols(name,data=data).fit()#建模 aic.append(result.aic)#將所有aic存入 if min(aic)>c0:#aic已經達到最小 data1 = pd.concat([df.iloc[:,i+1] for i in zhengshi ],axis = 1)#結合所需因子 name = "y~"+("+".join(data1.columns))#組成公式 break else: zhengshi.remove(all_bianliang[aic.index(min(aic))])#查找最小的aic並將最小的因子存入正式的模型列表當中 c0 = min(aic) delete.append(aic.index(min(aic))) all_bianliang.remove(all_bianliang[delete[-1]])#刪除已刪因子 name = "y~"+("+".join(data1.columns))#組成公式 print("最優模型為：{}，其aic為：{}".format(name,c0)) result = smf.ols(name,data=df).fit()#建模 print() print(result.summary())df = pd.read_csv("data3.1.csv",encoding='gbk')backward(df)（4）結果展示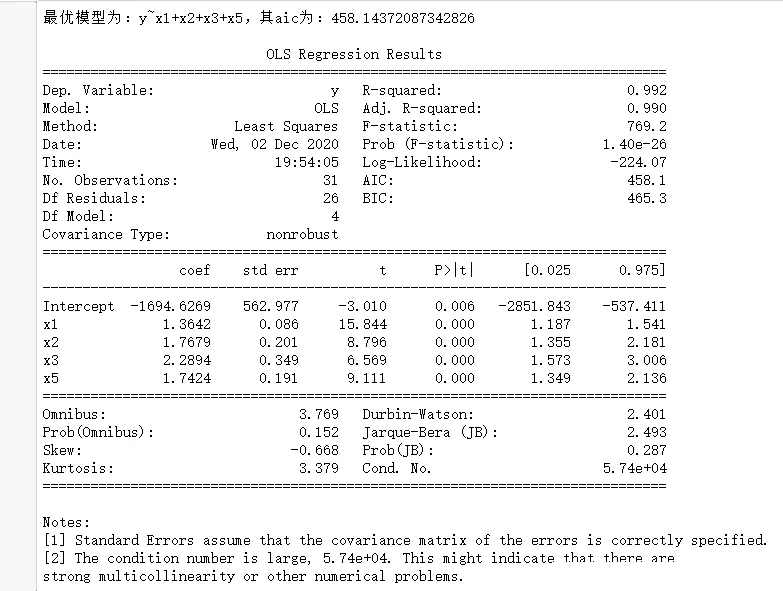
逐步回歸的基本思想是有進有出。R語言中step()函數的具體做法是在給定了包含p個變量的初始模型後，計算初始模型的AIC值，並在此模型基礎上分別剔除p個變量和添加剩余m-p個變量中的任一變量後的AIC值，然後選擇最小的AIC值決定是否添加新變量或剔除已存在初始模型中的變量。如此反復進行，直至既不添加新變量也不剔除模型中已有的變量時所對應的AIC值最小，即可停止計算，並返回最終結果。
（2）數據集情況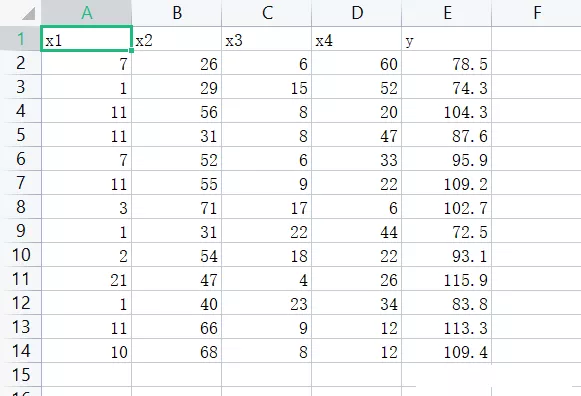
import pandas as pdimport numpy as npimport statsmodels.api as smimport statsmodels.formula.api as smfdef zhubuhuigui(df): forward = [i for i in range(0,4)]#備選因子 backward = []#備退因子 ceshi = []#存放加入單個因子後的模型 zhengshi = []#收集確定因子 delete = []#被刪因子 while forward: forward_aic = []#前進aic backward_aic = []#後退aic for i in forward: ceshi = [j for j in zhengshi] ceshi.append(i) data1 = pd.concat([df.iloc[:,i] for i in ceshi ],axis = 1)#結合所需因子 name = "y~"+("+".join(data1.columns))#組成公式 data = pd.concat([df['y'],data1],axis=1)#結合自變量和因變量 result = smf.ols(name,data=data).fit()#建模 forward_aic.append(result.aic)#將所有aic存入 for i in backward: if (len(backward)==1): pass else: ceshi = [j for j in zhengshi] ceshi.remove(i) data1 = pd.concat([df.iloc[:,i] for i in ceshi ],axis = 1)#結合所需因子 name = "y~"+("+".join(data1.columns))#組成公式 data = pd.concat([df['y'],data1],axis=1)#結合自變量和因變量 result = smf.ols(name,data=data).fit()#建模 backward_aic.append(result.aic)#將所有aic存入 if backward_aic: if forward_aic: c0 = min(min(backward_aic),min(forward_aic)) else: c0 = min(backward_aic) else: c0 = min(forward_aic) if c0 in backward_aic: zhengshi.remove(backward[backward_aic.index(c0)]) delete.append(backward_aic.index(c0)) backward.remove(backward[delete[-1]])#刪除已刪因子 forward.append(backward[delete[-1]]) else: zhengshi.append(forward[forward_aic.index(c0)])#查找最小的aic並將最小的因子存入正式的模型列表當中 forward.remove(zhengshi[-1])#刪除已有因子 backward.append(zhengshi[-1]) name = "y~"+("+".join(data1.columns))#組成公式 print("最優模型為：{}，其aic為：{}".format(name,c0)) result = smf.ols(name,data=data).fit()#建模 print() print(result.summary())df = pd.read_csv("data5.5.csv",encoding='gbk')zhubuhuigui(df)（4）結果展示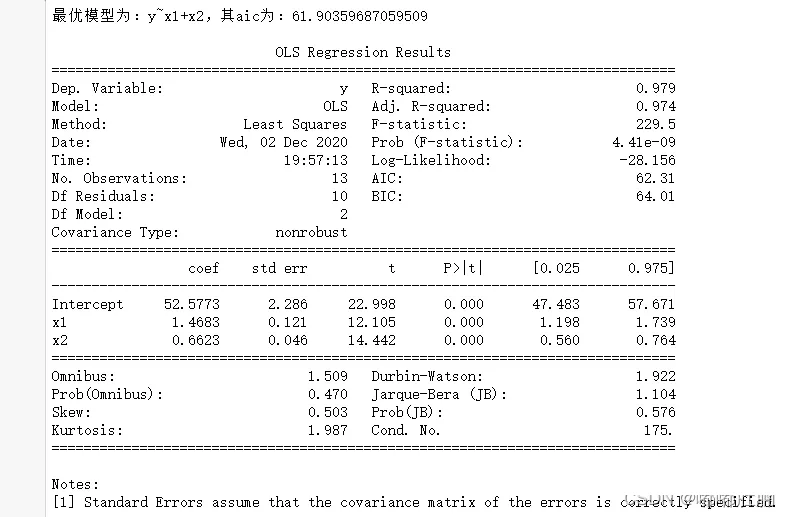
到此這篇關於python的自變量選擇(所有子集回歸,後退法,逐步回歸)的文章就介紹到這了,更多相關python自變量選擇內容請搜索軟件開發網以前的文章或繼續浏覽下面的相關文章希望大家以後多多支持軟件開發網！
Python crawler, whats the problem when you encounter this kind of problem? Is there any explanation for your tears
The running results are as fol
