Calculate the editing distance of the string (Python)

Levenshtein distance , Also called editing distance , Between two strings , By a transform
The minimum number of operations required for another , Permitted editing operations include replacing one character with another ,
Insert a character , Delete a character , The algorithm for editing distance was first developed by Russian scientists Levanshtein Proposed
So it's also called Levenshtein Distance.
for example ：
character string A ： abcdefg
character string B ： abcdef
By adding or deleting characters “g” The way to achieve the goal , Both schemes require one operation . Put this operation
The number of times required is defined as the distance between two strings .
requirement ： Given any string , Write an algorithm to calculate their editing distance .
Data range ： The given string length satisfies 1<= len(str) <= 10000
Input description ：
There are... In each use case 2 That's ok , Enter two strings for
Output description ：
Output one line for each use case , Represents the distance of the string
Example ：
Input ： abcdefg
abcdef
Output ： 1

• This is a dynamic programming problem , law Namely
• 1、 At some point It's about string_a and string_b Equal position , The edit distance at the change point is dp[row -1][col-1]
• 2、 If they are not equal, they are equal to the smallest of the three adjacent points plus +1
• After filling out the form ,srring_a To string_b The editing distance is dp[n][m]
  Fill in the form as shown in the following figure ：
  
  The code is as follows ：

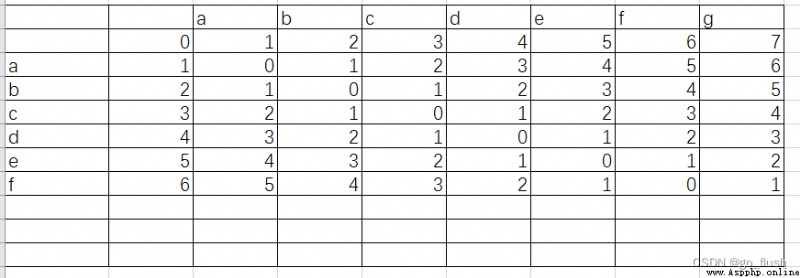
def edit_distance():
""" Edit distance """
string_a = input()
string_b = input()
m = len(string_a)
n = len(string_b)
dp = [[0 for _ in range(m + 1)] for _ in range(n + 1)]
# Change from empty position to string_a The distance of each position 
for col in range(m + 1):
dp[0][col] = col
# Change from empty position to string_b The distance of each position 
for row in range(n + 1):
dp[row][0] = row
# Fill in the form 
for row in range(1, n+1):
for col in range(1, m+1):
if string_a[col-1] != string_b[row-1]:
dp[row][col] = min(dp[row - 1][col], dp[row - 1][col-1], dp[row][col-1]) + 1
else:
dp[row][col] = dp[row-1][col-1]
print(dp[n][m])
if __name__ == '__main__':
edit_distance()