Python problem solving: street construction

The original title is

The big city of duvigas is designing one side of a new street . The street is divided into parcels of uniform size , Each block will be used as a house or park . The city is very proud of the number of parks it has , And no one needs to walk a long way to reach a beautiful park .

Specially , This city calls a group of continuous houses “ The block ”. The size of a block is the number of houses it contains .

According to the number of plots of new streets and the number of parks to be built , You need to determine the minimum size of the largest block that can be built .

Input

One line input , Contains two numbers , Number of parcels on the street N, And the number of parks to be built K, Separate... By spaces .1 ≤ K ≤ N ≤ 1,000,000,000

Output

A number , Represents the minimum size of the largest block that can be built .

Sample input 1

3 1

Sample output 1

1

explain 1

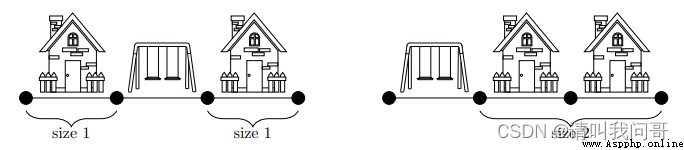
Consider the location of the park , There are two situations ： The park is built at both ends of the street , Or in the middle . If built at both ends of the street , The largest block size is 2; If it's in the middle , Both blocks are the size of 1. So the minimum size of the largest block is 1.

Sample input 2

3 3

Sample output 2

0

explain 2

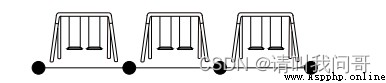
  Obvious , All plots are used as parks , Can't build a house , Therefore, the size of the block is 0.

Sample input 3

7 2

Sample output 3

2

explain 3

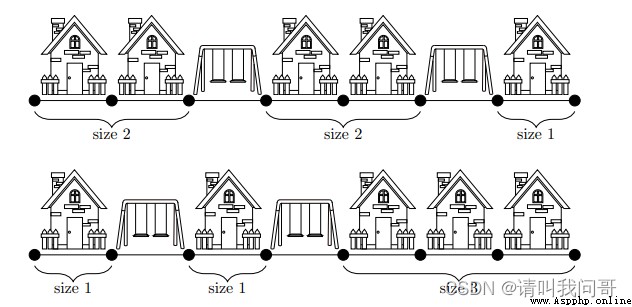
If you build a park every two houses , The available block size is 2,2,1, The largest block size is 2. If you build a park every other house , The available block size is 1,1,3, The largest block size is 3. therefore , The minimum size of the largest block is 2.

analysis

When I first saw this question, it may be a bit confusing , What is the minimum size of the largest block ？（ The original is the minimum possible size of the largest block） We can learn from the three examples given in the study topic , The size of the block depends on where the park is built , And the problem needs to be solved , By adjusting the location of the park , Make the size of the block as small as possible , And then in these blocks , Find the largest block size .

It's not hard to see. ,K A park can divide a continuous block into K+1 individual , For example 3 in ,2 A park 5 A house （7 Parcels minus 2 park ） It can be divided into the following possibilities （ Numbers indicate the size of each block ）. Except for the last two given in the example , You can also build parks together , However, the size of the largest plot is greater than or equal to 3, So there is no need to consider .

0,5,0

1,0,4

2,0,3

1,1,3

2,2,1

therefore , In order to achieve the goal , The best place to build the park , Is to be able to divide the blocks as evenly as possible , Then find out the biggest size in these blocks . So the mathematical solution , That is, the number of houses （N-K） Divide K+1, The result is rounded up .

Realization

Even simple upward forensics arithmetic , There are several ways to write code , The most intuitive is to use judgment statements ：

N, K = map(int,input().split())
if N<=K: res=0
else:
a = (N-K)//(K+1)
b = (N-K)%(K+1)
if b==0:
res=a
else:
res=a+1
print(res)

You can also use the built-in math Module ceil function , A statement calculates ：

N, K = map(int,input().split())
if N<=K: res=0
else:
import math
res = math.ceil((N-K)/(K+1))
print(res)

Of course , If not used math modular , You can also use bool Type data can be converted to and from integers （True=1, False=0）：

N, K = map(int,input().split())
if N<=K: res=0
else: res=(N-K)//(K+1)+bool((N-K)%(K+1))
print(res)