Python解題：街道建設

原題

大城市杜維加斯正在設計一條新街道的一側。這條街被分割成大小均勻的地塊，每一塊都將用作住宅或公園。這座城市對它擁有的公園數量感到非常自豪，而且沒有人需要走很遠的路才能到達某個美麗的公園。

特別地，這個城市把一組連續的住宅稱為“街區”。一個街區的大小就是它所包含的住宅數量。

根據新街道的地塊數量以及將要建造的公園數量，你需要確定可以建設的最大街區的最小尺寸。

輸入

一行輸入，包含兩個數字，街道上地塊的數量N，以及將建設的公園數量K，以空格分開。1 ≤ K ≤ N ≤ 1,000,000,000

輸出

一個數字，表示可以建設的最大街區的最小尺寸。

示例輸入1

3 1

示例輸出1

1

解釋1

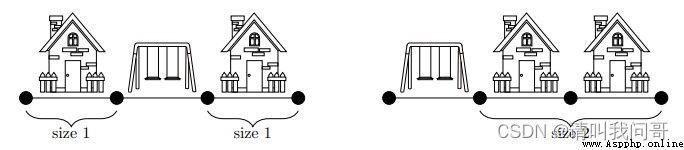
考慮建造公園的位置，有兩種情況：公園建造在街道的兩端，或者是中間。如果建造在街道兩端，最大街區的大小為2；如果在中間，兩個街區的大小都是1。所以最大街區的最小尺寸為1。

示例輸入2

3 3

示例輸出2

0

解釋2

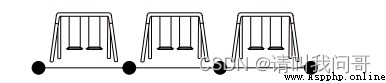
 顯而易見，所有地塊都被用作公園，無法建造住宅，故街區的尺寸為0。

示例輸入3

7 2

示例輸出3

2

解釋3

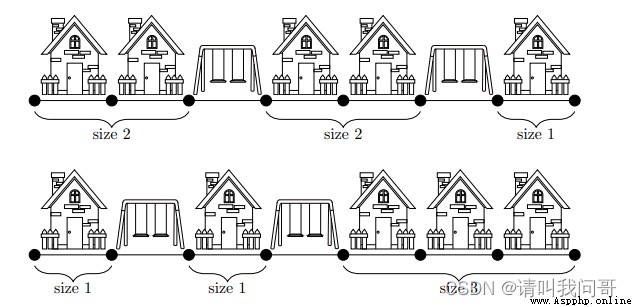
如果每隔兩棟住宅建造一個公園，可以得到的街區尺寸是2,2,1，最大街區的尺寸是2。如果每隔一棟住宅建造一個公園，可以得到的街區尺寸是1,1,3，最大街區的尺寸是3。所以，最大街區的最小尺寸是2。

分析

剛見到這題的時候可能會有些讓人摸不著頭腦，什麼叫最大街區的最小尺寸？（原文是the minimum possible size of the largest block）通過學習題目給的三個例子可以得知，街區的尺寸大小取決於建造公園的位置，而題目要求解決的，就是通過調整公園的位置，把街區的尺寸都盡量變小，然後在這些街區裡，找到最大的街區尺寸。

不難看出，K個公園可以把連續的街區分成K+1個，比如例3中，2個公園把5個住宅（7地塊減去2公園）可以分成以下幾種可能（數字表示每個街區的尺寸）。除了例子中給出的最後兩種，還可以把公園建造在一起，但這也得到的最大地塊的尺寸都大於等於3，所以更加不用考慮。

0,5,0

1,0,4

2,0,3

1,1,3

2,2,1

所以，為了實現目標，最佳的公園建造位置，就是能夠把街區盡可能地平均分隔開，然後找出這些街區裡最大的尺寸。所以數學上的解法，就是把住宅數量（N-K）除以K+1，得到的結果向上取整。

實現

即使是簡單的向上取證的算術，使用代碼也可以有幾種寫法，最直觀的就是使用判斷語句：

N, K = map(int,input().split())
if N<=K: res=0
else:
a = (N-K)//(K+1)
b = (N-K)%(K+1)
if b==0:
res=a
else:
res=a+1
print(res)

也可以使用內置的math模塊中ceil函數，一條語句計算：

N, K = map(int,input().split())
if N<=K: res=0
else:
import math
res = math.ceil((N-K)/(K+1))
print(res)

當然，如果不使用math模塊，也可以利用bool型數據可以與整數互相轉換的特性來實現（True=1, False=0）：

N, K = map(int,input().split())
if N<=K: res=0
else: res=(N-K)//(K+1)+bool((N-K)%(K+1))
print(res)