Précédent
Dubins Calcul de la courbe ( Approche vectorielle )
Ce qui précède a été fait du point de vue vectoriel Dubins Dérivation de la formule de courbe , Ce blog est basé principalement sur cet article 《Classification of the Dubins set》 Introduction aux relations géométriques dubins Formule de courbe , Il y a une dérivation détaillée pour chaque cas , Par conséquent, seule la formule pour chaque cas est donnée ici. , Tout le monde peut se référer à la thèse pour le processus de dérivation. .
dubins La collection de chemins est { L S L , R S R , R S L , L S R , R L R , L R L } \{LSL, RSR, RSL, LSR, RLR, LRL\} { LSL,RSR,RSL,LSR,RLR,LRL}. L L L Représente le mouvement de l'arc vers la gauche , R R R Représente le mouvement de l'arc tournant à droite , S S S Représente le mouvement en ligne droite .
Réglez le point de départ à s ( x i , y i , α i ) s\left(x_{i}, y_{i}, \alpha_{i}\right) s(xi,yi,αi) ,Le point final est g ( x g , y g , β g ) g\left(x_{g}, y_{g}, \beta_{g}\right) g(xg,yg,βg) , La première transformation de coordonnées traduit le point de départ à l'origine ,Et tourne θ \theta θ Angle, Et la fin tombe x \mathrm{x} x Sur l'axe, Les coordonnées de départ et de fin sont: s ( 0 , 0 , α ) , g ( d , 0 , β ) s(0,0, \alpha), g(d, 0, \beta) s(0,0,α),g(d,0,β) ,Parmi eux:
θ = atan 2 ( y g − y i x g − x i ) m o d { 2 π } D = ( x i − x g ) 2 + ( y i − y g ) 2 d = D / R α = ( α i − θ ) m o d { 2 π } β = ( β g − θ ) m o d { 2 π } (1) \tag{1} \begin{gathered} \theta=\operatorname{atan} 2\left(\frac{y_{g}-y_{i}}{x_{g}-x_{i}}\right) \bmod\{2\pi\} \\ D=\sqrt{\left(x_{i}-x_{g}\right)^{2}+\left(y_{i}-y_{g}\right)^{2}} \\ d=D / R \\ \alpha= \left(\alpha_{i}-\theta\right) \bmod\{2\pi\} \\ \beta= \left(\beta_{g}-\theta\right) \bmod\{2\pi\} \end{gathered} θ=atan2(xg−xiyg−yi)mod{ 2π}D=(xi−xg)2+(yi−yg)2d=D/Rα=(αi−θ)mod{ 2π}β=(βg−θ)mod{ 2π}(1)
Quelques remarques:
Parmi eux θ \theta θ Différence d'angle de cap entre le début et la fin , Tous les angles sont là - haut. [ 0 , 2 π ] [0,2 \pi] [0,2π] Entre.
C'est pour ça. D D D À part ça. R R R Ceci permet de faire chaque rayon de virage minimal R R RTous. 1 , Il est plus pratique de calculer la longueur d'arc à partir de l'angle , La longueur de l'arc est un radian égal à l'angle , Donc ce que j'ai vu plus loin cos ( α ) \cos (\alpha) cos(α) , En fait, c'est omis. R R R .
m o d ( ) mod() mod()C'est une opération modulaire,Par exemple: m o d ( 3 π , 2 π ) = 3 π m o d 2 π = π \bmod(3\pi,2\pi)=3\pi \bmod 2 \pi=\pi mod(3π,2π)=3πmod2π=π.Comme suit: β ( m o d 2 π ) \beta(\bmod 2 \pi) β(mod2π)C'est ce que ça veut dire.,C'est - à - dire: β \beta βC'est exact. 2 π 2\pi 2πPrendre le moule.pythonLa mise en œuvre est simple,Comme suit:
def mod2pi(theta):
"""C'est exact.2piOpérations modulaires """
return theta - 2.0 * math.pi * math.floor(theta / 2.0 / math.pi)
Coordonnées transformées pythonLa mise en œuvre est simple,Comme suit:
# Transformation des coordonnées
dx = g_x-s_x
dy = g_y-s_y
D = math.hypot(dx, dy)
d = D * curvature
theta = mod2pi(math.atan2(dy, dx))
alpha = mod2pi(s_yaw - theta)
beta = mod2pi(g_yaw - theta)
Régler la longueur parcourue par le véhicule sur le cercle de départ comme suit: t t t , La longueur du segment droit est p p p , La longueur de l'arc sur le deuxième cercle est q q q, Longueur totale du chemin L = t + p + q L=t+p+q L=t+p+q.On trouvera ci - après une liste de6 Formule de trajectoire pour chaque cas .

L S L LSL LSL La formule de longueur de piste du chemin est la suivante: :
t l s l = − α + arctan cos β − cos α d + sin α − sin β { m o d 2 π } p l s l = 2 + d 2 − 2 cos ( α − β ) + 2 d ( sin α − sin β ) q l s l = β − arctan cos β − cos α d + sin α − sin β { m o d 2 π } (2) \tag{2} \begin{aligned} &t_{l s l}=-\alpha+\arctan \frac{\cos \beta-\cos \alpha}{d+\sin \alpha-\sin \beta}\{\bmod 2 \pi\} \\ &p_{l s l}=\sqrt{2+d^{2}-2 \cos (\alpha-\beta)+2 d(\sin \alpha-\sin \beta)} \\ &q_{l s l}=\beta-\arctan \frac{\cos \beta-\cos \alpha}{d+\sin \alpha-\sin \beta}\{\bmod 2 \pi\} \end{aligned} tlsl=−α+arctand+sinα−sinβcosβ−cosα{ mod2π}plsl=2+d2−2cos(α−β)+2d(sinα−sinβ)qlsl=β−arctand+sinα−sinβcosβ−cosα{ mod2π}(2)
La longueur totale est égale à :
L l s l = t l s l + p l s l + q l s l = − α + β + p l s l (3) \tag{3} \mathcal{L}_{l s l}=t_{l s l}+p_{l s l}+q_{l s l}=-\alpha+\beta+p_{l s l} Llsl=tlsl+plsl+qlsl=−α+β+plsl(3)
pythonLa réalisation est la suivante:
def left_straight_left(alpha, beta, d):
"""LSLChemin """
sa = math.sin(alpha)
sb = math.sin(beta)
ca = math.cos(alpha)
cb = math.cos(beta)
c_ab = math.cos(alpha - beta)
tmp0 = d + sa - sb
mode = ["L", "S", "L"]
p_squared = 2 + (d * d) - (2 * c_ab) + (2 * d * (sa - sb))
if p_squared < 0:
return None, None, None, mode
tmp1 = math.atan2((cb - ca), tmp0)
t = mod2pi(-alpha + tmp1)
p = math.sqrt(p_squared)
q = mod2pi(beta - tmp1)
return t, p, q, mode
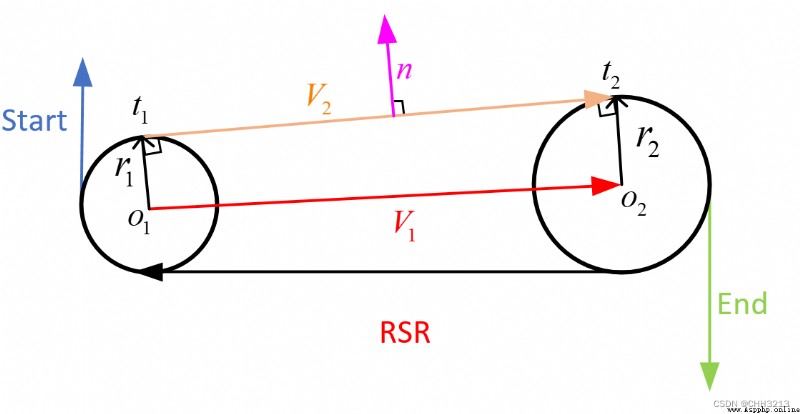
R S R RSR RSR La formule de longueur de piste du chemin est la suivante: :
t r s r = α − arctan cos α − cos β d − sin α + sin β { m o d 2 π } p r s r = 2 + d 2 − 2 cos ( α − β ) + 2 d ( sin β − sin α ) q r s r = − β ( m o d 2 π ) + arctan cos α − cos β d − sin α + sin β { m o d 2 π } (4) \tag{4} \begin{aligned} t_{r s r} &=\alpha-\arctan \frac{\cos \alpha-\cos \beta}{d-\sin \alpha+\sin \beta}\{\bmod 2 \pi\} \\ p_{r s r} &=\sqrt{2+d^{2}-2 \cos (\alpha-\beta)+2 d(\sin \beta-\sin \alpha)} \\ q_{r s r} &=-\beta(\bmod 2 \pi)+\arctan \frac{\cos \alpha-\cos \beta}{d-\sin \alpha+\sin \beta}\{\bmod 2 \pi\} \\ \end{aligned} trsrprsrqrsr=α−arctand−sinα+sinβcosα−cosβ{ mod2π}=2+d2−2cos(α−β)+2d(sinβ−sinα)=−β(mod2π)+arctand−sinα+sinβcosα−cosβ{ mod2π}(4)
La longueur totale est égale à :
L r s r = t r s r + p r s r + q r s r = α − β + p r s r (5) \tag{5} \mathcal{L}_{r s r} =t_{r s r}+p_{r s r}+q_{r s r}=\alpha-\beta+p_{r s r} Lrsr=trsr+prsr+qrsr=α−β+prsr(5)
pythonLa réalisation est la suivante:
def right_straight_right(alpha, beta, d):
"""RSRChemin """
sa = math.sin(alpha)
sb = math.sin(beta)
ca = math.cos(alpha)
cb = math.cos(beta)
c_ab = math.cos(alpha - beta)
tmp0 = d - sa + sb
mode = ["R", "S", "R"]
p_squared = 2 + (d * d) - (2 * c_ab) + (2 * d * (sb - sa))
if p_squared < 0:
return None, None, None, mode
tmp1 = math.atan2((ca - cb), tmp0)
t = mod2pi(alpha - tmp1)
p = math.sqrt(p_squared)
q = mod2pi(-mod2pi(beta) + tmp1)
return t, p, q, mode
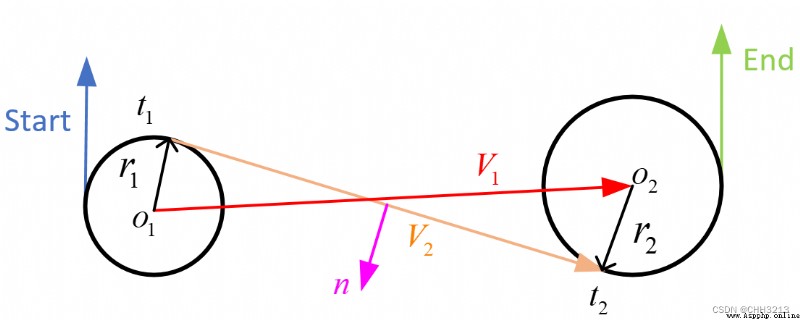
R S L RSL RSL La formule de longueur de piste du chemin est la suivante: :
t r s l = α − arctan ( cos α + cos β d − sin α − sin β ) + arctan ( 2 p r s l ) { m o d 2 π } p r s l = d 2 − 2 + 2 cos ( α − β ) − 2 d ( sin α + sin β ) q r s l = β ( m o d 2 π ) − arctan ( cos α + cos β d − sin α − sin β ) + arctan ( 2 p r s l ) { m o d 2 π } (6) \tag{6} \begin{aligned} t_{r s l} &=\alpha-\arctan \left(\frac{\cos \alpha+\cos \beta}{d-\sin \alpha-\sin \beta}\right)+\arctan \left(\frac{2}{p_{r s l}}\right)\{\bmod 2 \pi\} \\ p_{r s l} &=\sqrt{d^{2}-2+2 \cos (\alpha-\beta)-2 d(\sin \alpha+\sin \beta)} \\ q_{r s l} &=\beta(\bmod 2 \pi)-\arctan \left(\frac{\cos \alpha+\cos \beta}{d-\sin \alpha-\sin \beta}\right)+\arctan \left(\frac{2}{p_{r s l}}\right)\{\bmod 2 \pi\} \\ \end{aligned} trslprslqrsl=α−arctan(d−sinα−sinβcosα+cosβ)+arctan(prsl2){ mod2π}=d2−2+2cos(α−β)−2d(sinα+sinβ)=β(mod2π)−arctan(d−sinα−sinβcosα+cosβ)+arctan(prsl2){ mod2π}(6)
La longueur totale est égale à :
L r s l = t r s l + p r s l + q r s l = − α + β + 2 t r s l + p r s l (7) \tag{7} \mathcal{L}_{r s l} =t_{r s l}+p_{r s l}+q_{r s l}=-\alpha+\beta+2 t_{r s l}+p_{r s l} Lrsl=trsl+prsl+qrsl=−α+β+2trsl+prsl(7)
pythonLa réalisation est la suivante:
def right_straight_left(alpha, beta, d):
"""RSLChemin """
sa = math.sin(alpha)
sb = math.sin(beta)
ca = math.cos(alpha)
cb = math.cos(beta)
c_ab = math.cos(alpha - beta)
p_squared = (d * d) - 2 + (2 * c_ab) - (2 * d * (sa + sb))
mode = ["R", "S", "L"]
if p_squared < 0:
return None, None, None, mode
p = math.sqrt(p_squared)
tmp2 = math.atan2((ca + cb), (d - sa - sb)) - math.atan2(2.0, p)
t = mod2pi(alpha - tmp2)
q = mod2pi(mod2pi(beta) - tmp2)
return t, p, q, mode
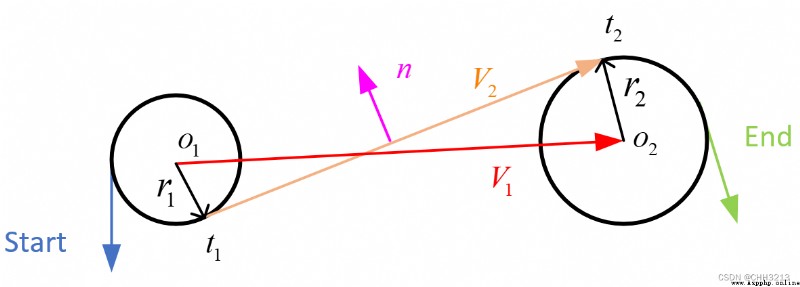
L S R LSR LSR La formule de longueur de piste du chemin est la suivante: :
t l s r = ( − α + arctan ( − cos α − cos β d + sin α + sin β ) − arctan ( − 2 p l s r ) ) { m o d 2 π } p l s r = − 2 + d 2 + 2 cos ( α − β ) + 2 d ( sin α + sin β ) q l s r = − β ( m o d 2 π ) + arctan ( − cos α − cos β d + sin α + sin β ) − arctan ( − 2 p l s r ) { m o d 2 π } (8) \tag{8} \begin{aligned} t_{l s r} &=\left(-\alpha+\arctan \left(\frac{-\cos \alpha-\cos \beta}{d+\sin \alpha+\sin \beta}\right)-\arctan \left(\frac{-2}{p_{l s r}}\right)\right)\{\bmod 2 \pi\} \\ p_{l s r} &=\sqrt{-2+d^{2}+2 \cos (\alpha-\beta)+2 d(\sin \alpha+\sin \beta)} \\ q_{l s r} &=-\beta(\bmod 2 \pi)+\arctan \left(\frac{-\cos \alpha-\cos \beta}{d+\sin \alpha+\sin \beta}\right)-\arctan \left(\frac{-2}{p_{l s r}}\right)\{\bmod 2 \pi\} \\ \end{aligned} tlsrplsrqlsr=(−α+arctan(d+sinα+sinβ−cosα−cosβ)−arctan(plsr−2)){ mod2π}=−2+d2+2cos(α−β)+2d(sinα+sinβ)=−β(mod2π)+arctan(d+sinα+sinβ−cosα−cosβ)−arctan(plsr−2){ mod2π}(8)
La longueur totale est égale à :
L l s r = t l s r + p l s r + q l s r = α − β + 2 t l s r + p l s r (9) \tag{9} \mathcal{L}_{l s r} =t_{l s r}+p_{l s r}+q_{l s r}=\alpha-\beta+2 t_{l s r}+p_{l s r} Llsr=tlsr+plsr+qlsr=α−β+2tlsr+plsr(9)
pythonLa réalisation est la suivante:
def left_straight_right(alpha, beta, d):
"""LSRChemin """
sa = math.sin(alpha)
sb = math.sin(beta)
ca = math.cos(alpha)
cb = math.cos(beta)
c_ab = math.cos(alpha - beta)
p_squared = -2 + (d * d) + (2 * c_ab) + (2 * d * (sa + sb))
mode = ["L", "S", "R"]
if p_squared < 0:
return None, None, None, mode
p = math.sqrt(p_squared)
tmp2 = math.atan2((-ca - cb), (d + sa + sb)) - math.atan2(-2.0, p)
t = mod2pi(-alpha + tmp2)
q = mod2pi(-mod2pi(beta) + tmp2)
return t, p, q, mode
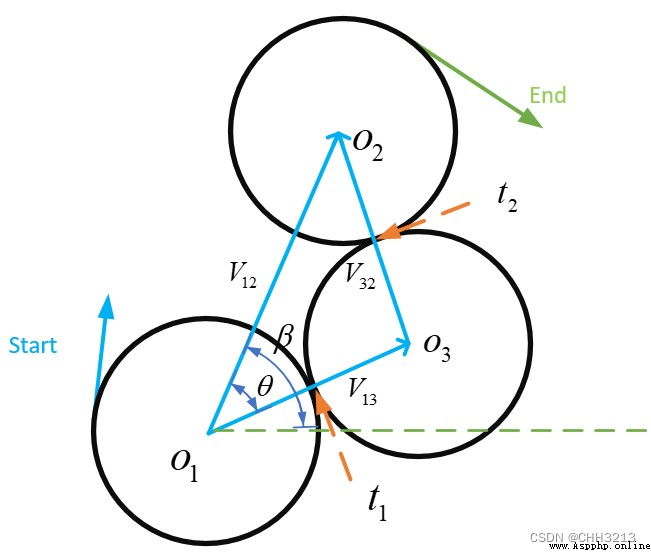
R L R RLR RLR La formule de longueur de piste du chemin est la suivante: :
t r l r = α − arctan ( cos α − cos β d − sin α + sin β ) + p r l r 2 { m o d 2 π } p r l r = arccos 1 8 ( 6 − d 2 + 2 cos ( α − β ) + 2 d ( sin α − sin β ) ) q r l r = α − β − t r l r + p r l r { m o d 2 π } (10) \tag{10} \begin{aligned} &t_{r l r}=\alpha-\arctan \left(\frac{\cos \alpha-\cos \beta}{d-\sin \alpha+\sin \beta}\right)+\frac{p_{r l r}}{2}\{\bmod 2 \pi\} \\ &p_{r l r}=\arccos \frac{1}{8}\left(6-d^{2}+2 \cos (\alpha-\beta)+2 d(\sin \alpha-\sin \beta)\right) \\ &q_{r l r}=\alpha-\beta-t_{r l r}+p_{r l r}\{\bmod 2 \pi\} \\ \end{aligned} trlr=α−arctan(d−sinα+sinβcosα−cosβ)+2prlr{ mod2π}prlr=arccos81(6−d2+2cos(α−β)+2d(sinα−sinβ))qrlr=α−β−trlr+prlr{ mod2π}(10)
La longueur totale est égale à :
L r l r = t r l r + p r l r + q r l r = α − β + 2 p r l r (11) \tag{11} \mathcal{L}_{r l r}=t_{r l r}+p_{r l r}+q_{r l r}=\alpha-\beta+2 p_{r l r} Lrlr=trlr+prlr+qrlr=α−β+2prlr(11)
pythonLa réalisation est la suivante:
def right_left_right(alpha, beta, d):
"""RLRChemin """
sa = math.sin(alpha)
sb = math.sin(beta)
ca = math.cos(alpha)
cb = math.cos(beta)
c_ab = math.cos(alpha - beta)
mode = ["R", "L", "R"]
tmp_rlr = (6.0 - d * d + 2.0 * c_ab + 2.0 * d * (sa - sb)) / 8.0
if abs(tmp_rlr) > 1.0:
return None, None, None, mode
p = mod2pi(math.acos(tmp_rlr))
t = mod2pi(alpha - math.atan2(ca - cb, d - sa + sb) + mod2pi(p / 2.0))
q = mod2pi(alpha - beta - t + p)
return t, p, q, mode
Les méthodes de mise en œuvre ci - dessus n'obtiennent pas de résultats optimaux ,C'est étrange, L'écriture suivante donne les meilleurs résultats :
def right_left_right(alpha, beta, d):
"""RLRChemin, La mise en œuvre de cette partie n'est pas conforme à la formule , Il n'y a pas de chemin optimal après avoir été modifié pour être conforme à la formule """
sa = math.sin(alpha)
sb = math.sin(beta)
ca = math.cos(alpha)
cb = math.cos(beta)
c_ab = math.cos(alpha - beta)
mode = ["R", "L", "R"]
tmp_rlr = (6.0 - d * d + 2.0 * c_ab + 2.0 * d * (sa - sb)) / 8.0
if abs(tmp_rlr) > 1.0:
return None, None, None, mode
p = mod2pi(2 * math.pi - math.acos(tmp_rlr))
t = mod2pi(alpha - math.atan2(ca - cb, d - sa + sb) + mod2pi(p / 2.0))
q = mod2pi(alpha - beta - t + mod2pi(p))
return t, p, q, mode
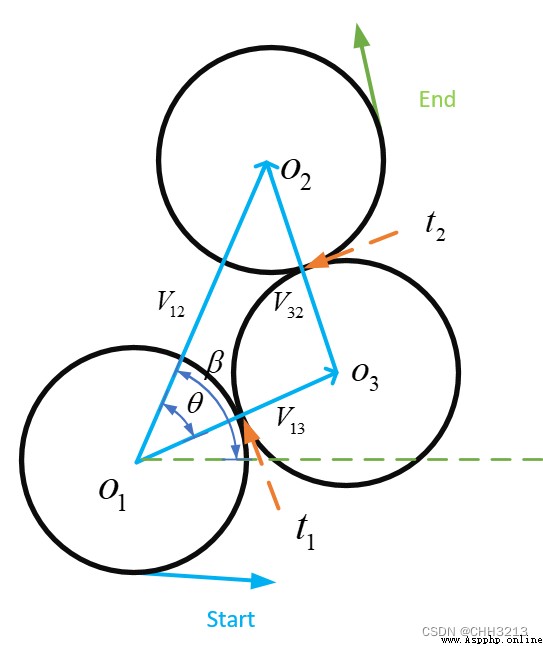
L R L LRL LRL La formule de longueur de piste du chemin est la suivante: :
t l r l = ( − α + arctan ( − cos α + cos α d + sin α − sin β ) + p l r l 2 ) { m o d 2 π } p l r l = arccos 1 8 ( 6 − d 2 + 2 cos ( α − β ) + 2 d ( sin α − sin β ) ) { m o d 2 π } q l r l = β ( m o d 2 π ) − α + 2 p l r l { m o d 2 π } (12) \tag{12} \begin{aligned} &t_{l r l}=\left(-\alpha+\arctan \left(\frac{-\cos \alpha+\cos \alpha}{d+\sin \alpha-\sin \beta}\right)+\frac{p_{l r l}}{2}\right)\{\bmod 2 \pi\} \\ &p_{l r l}=\arccos \frac{1}{8}\left(6-d^{2}+2 \cos (\alpha-\beta)+2 d(\sin \alpha-\sin \beta)\right)\{\bmod 2 \pi\} \\ &q_{l r l}=\beta(\bmod 2 \pi)-\alpha+2 p_{l r l}\{\bmod 2 \pi\} \end{aligned} tlrl=(−α+arctan(d+sinα−sinβ−cosα+cosα)+2plrl){ mod2π}plrl=arccos81(6−d2+2cos(α−β)+2d(sinα−sinβ)){ mod2π}qlrl=β(mod2π)−α+2plrl{ mod2π}(12)
La longueur totale est égale à :
L l r l = t l r l + p l r l + q l r l = − α + β + 2 p l r l . (13) \tag{13} \mathcal{L}_{l r l}=t_{l r l}+p_{l r l}+q_{l r l}=-\alpha+\beta+2 p_{l r l} . Llrl=tlrl+plrl+qlrl=−α+β+2plrl.(13)
pythonLa réalisation est la suivante:
def left_right_left(alpha, beta, d):
"""LRLChemin """
sa = math.sin(alpha)
sb = math.sin(beta)
ca = math.cos(alpha)
cb = math.cos(beta)
c_ab = math.cos(alpha - beta)
mode = ["L", "R", "L"]
tmp_lrl = (6.0 - d * d + 2.0 * c_ab + 2.0 * d * (- sa + sb)) / 8.0
if abs(tmp_lrl) > 1:
return None, None, None, mode
p = mod2pi(math.acos(tmp_lrl))
t = mod2pi(-alpha - math.atan2(ca - cb, d + sa - sb) + p / 2.0)
q = mod2pi(mod2pi(beta) - alpha +2*p)
return t, p, q, mode
De même, les méthodes de mise en œuvre ci - dessus n'obtiennent pas de résultats optimaux. , L'écriture suivante donne les meilleurs résultats :
def left_right_left(alpha, beta, d):
"""LRLChemin, La mise en œuvre de cette partie n'est pas conforme à la formule , Il n'y a pas de chemin optimal après avoir été modifié pour être conforme à la formule """
sa = math.sin(alpha)
sb = math.sin(beta)
ca = math.cos(alpha)
cb = math.cos(beta)
c_ab = math.cos(alpha - beta)
mode = ["L", "R", "L"]
tmp_lrl = (6.0 - d * d + 2.0 * c_ab + 2.0 * d * (- sa + sb)) / 8.0
if abs(tmp_lrl) > 1:
return None, None, None, mode
p = mod2pi(2 * math.pi - math.acos(tmp_lrl))
t = mod2pi(-alpha - math.atan2(ca - cb, d + sa - sb) + p / 2.0)
q = mod2pi(mod2pi(beta) - alpha - t + mod2pi(p))
return t, p, q, mode
Voir le code complet ci - dessus githubEntrepôt
 Cloud Computing Development: detailed explanation of python3 trigonometric function asin() method
Cloud Computing Development: detailed explanation of python3 trigonometric function asin() method
describe Python3 asin() return
 Python matplotlib. pyplot. An example of hist() histogram drawing method
Python matplotlib. pyplot. An example of hist() histogram drawing method
Catalog One 、matplotlib.pyplo