Size constrained clustering problem

1 The main method

# Import library
from size_constrained_clustering import fcm, equal, minmax, shrinkage,da
# by default it is euclidean distance, but can select others
from sklearn.metrics.pairwise import haversine_distances
from sklearn.datasets import make_blobs
import numpy as np
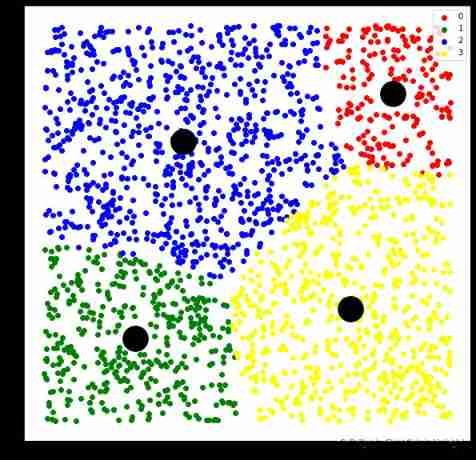
import matplotlib.pyplot as plt

1.1 Fuzzy C-means Algorithm

and KMeans similar , But using the attribution probability （membership probability） Calculate , Not directly 0 perhaps 1

n_samples = 2000
n_clusters = 4
centers = [(-5, -5), (0, 0), (5, 5), (7, 10)]
X, _ = make_blobs(n_samples=n_samples, n_features=2, cluster_std=1.0,
centers=centers, shuffle=False, random_state=42)
# Generate data set , Each main sentence has two eigenvalues , altogether 2000 Samples , Four categories , At the same time, the position of the cluster center is set
model = fcm.FCM(n_clusters)
# use other distance function: e.g. haversine distance
# model = fcm.FCM(n_clusters, distance_func=haversine_distances)
model.fit(X)
centers = model.cluster_centers_
'''
array([[ 0.06913083, 0.07352352],
[-5.01038079, -4.98275774],
[ 6.99974221, 10.01169349],
[ 4.98686053, 5.0026792 ]])
After model fitting , The central point of sample clustering
'''
labels = model.labels_
# After model fitting , Category of each sample 

plt.figure(figsize=(10,10))
colors=['red','green','blue','yellow']
for i,color in enumerate(colors):
color_tmp=np.where(labels==i)[0]
plt.scatter(X[color_tmp,0],X[color_tmp,1],c=color,label=i)
plt.legend()
plt.scatter(centers[:,0],centers[:,1],s=1000,c='black')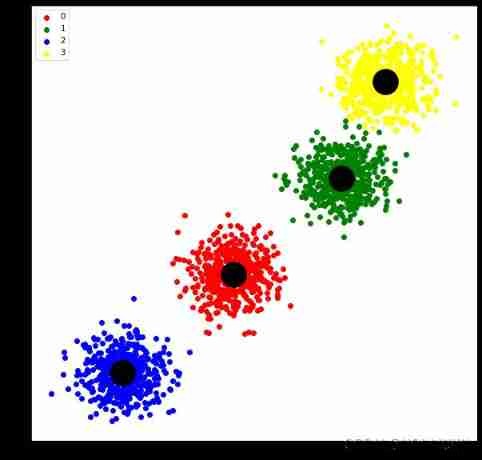

1. 2 Same Size Contrained KMeans Heuristics

Using heuristic method to obtain equal size clustering results

n_samples = 2000
n_clusters = 4
X = np.random.rand(n_samples, 2)
# use minimum cost flow framework to solve
model = equal.SameSizeKMeansHeuristics(n_clusters)
model.fit(X)
centers = model.cluster_centers_
labels = model.labels_

import matplotlib.pyplot as plt
plt.figure(figsize=(10,10))
colors=['red','green','blue','yellow']
for i,color in enumerate(colors):
color_tmp=np.where(labels==i)[0]
plt.scatter(X[color_tmp,0],X[color_tmp,1],c=color,label=i)
plt.legend()
plt.scatter(centers[:,0],centers[:,1],s=1000,c='black')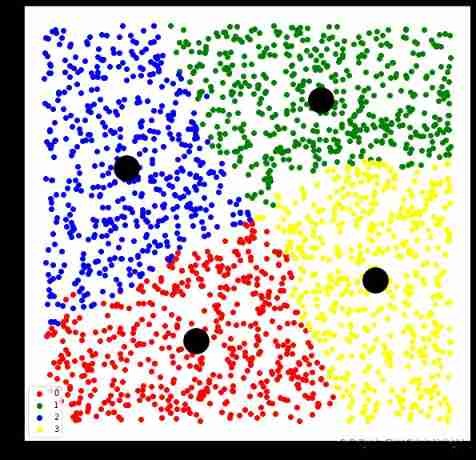

1.3 Same Size Contrained KMeans Inspired by Minimum Cost Flow Problem：

Transform clustering into assignment problem , And use the idea of minimum cost flow to solve

n_samples = 2000
n_clusters = 4
X = np.random.rand(n_samples, 2)
# use minimum cost flow framework to solve
model = equal.SameSizeKMeansMinCostFlow(n_clusters)
model.fit(X)
centers = model.cluster_centers_
labels = model.labels_

plt.figure(figsize=(10,10))
colors=['red','green','blue','yellow']
for i,color in enumerate(colors):
color_tmp=np.where(labels==i)[0]
plt.scatter(X[color_tmp,0],X[color_tmp,1],c=color,label=i)
plt.legend()
plt.scatter(centers[:,0],centers[:,1],s=1000,c='black')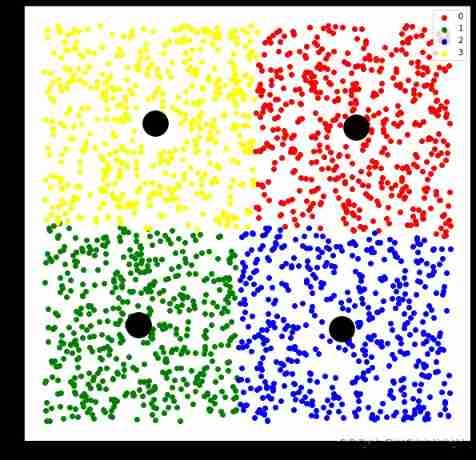

1.4 Minimum and Maximum Size Constrained KMeans Inspired by Minimum Cost Flow Problem

Transform clustering into assignment problem , And use the idea of minimum cost flow to solve , Add the minimum and maximum cluster size restrictions

n_samples = 2000
n_clusters = 4
X = np.random.rand(n_samples, 2)
# use minimum cost flow framework to solve
model = minmax.MinMaxKMeansMinCostFlow(
n_clusters,
size_min=200,
size_max=800)
model.fit(X)
centers = model.cluster_centers_
labels = model.labels_
plt.figure(figsize=(10,10))
colors=['red','green','blue','yellow']
for i,color in enumerate(colors):
color_tmp=np.where(labels==i)[0]
plt.scatter(X[color_tmp,0],X[color_tmp,1],c=color,label=i)
plt.legend()
plt.scatter(centers[:,0],centers[:,1],s=1000,c='black')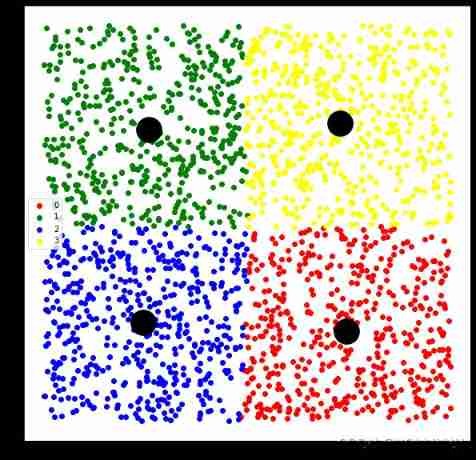

1.5 Deterministic Annealling Algorithm:

Enter the scale proportion of each type of target , Get the results of the corresponding cluster size .

n_samples = 2000
n_clusters = 4
X = np.random.rand(n_samples, 2)
# use minimum cost flow framework to solve
model = da.DeterministicAnnealing(
n_clusters,
distribution=[0.1, 0.2,0.4, 0.3])
model.fit(X)
centers = model.cluster_centers_
labels = model.labels_
plt.figure(figsize=(10,10))
colors=['red','green','blue','yellow']
for i,color in enumerate(colors):
color_tmp=np.where(labels==i)[0]
plt.scatter(X[color_tmp,0],X[color_tmp,1],c=color,label=i)
plt.legend()
plt.scatter(centers[:,0],centers[:,1],s=1000,c='black')