您现在的位置：程式師世界 >> 編程語言 > >> 更多編程語言 >> Python

基於單層決策樹的AdaBoost算法原理+python實現

編輯：Python

這裡整理一下實驗課實現的基於單層決策樹的弱分類器的AdaBoost算法。

由於是初學，實驗課在找資料的時候看到別人的代碼中有太多英文的縮寫，不容易看懂，而且還要同時看代碼實現的細節、算法的原理什麼的，就體驗很不好。

於是我這裡代碼中英文沒有用縮寫，也盡量把思路寫清楚。

基本概念

集成學習：通過組合多個基分類器（base classifier）來完成學習任務，基分類器一般采用弱學習器。
弱學習器：只學習正確率僅僅略優於隨機猜測的學習器。通過集成方法，就能組合成一個強學習器。
Bagging和Boosting：集成學習主要的兩種把弱分類器組裝成強分類器的方法。
AdaBoost是adaptive boosting的縮寫。
Bagging：從原始數據集中有放回地抽訓練集，每輪訓練集之間是獨立的。每次使用一個訓練集得到一個模型。分類問題就讓這些模型投票得到分類結果，回歸問題就算這些模型的均值。
Boosting：每一輪的訓練集不變，只是訓練集中每個樣本在分類器中的權重發生變化，並且每一輪的樣本的權重分布依賴上一輪的分類結果。每個弱分類器也都有各自的權重，分類誤差小的分類器有更大的權重。
舉個例子：Bagging+決策樹=隨機森林；Boosting+決策樹=提升樹
AdaBoost：計算樣本權重->計算錯誤率->計算弱學習器的權重->更新樣本權重...重復。

原理+代碼實現

就是構造弱分類器，再根據一定方法組裝起來。

from numpy import *

加載數據集

用的是實驗課給的數據集(horseColic 馬疝病數據集)...這部分不多說了。帶_array後綴的是列表，帶_matrix後綴的是把相應array變成的np矩陣。

def load_dataset(filename):
num_feature = len(open(filename).readline().split('\t'))
data_array = []
label_array = []
f = open(filename)
for line in f.readlines():
line_array = []
current_line = line.strip().split('\t')
for i in range(num_feature - 1):
line_array.append(float(current_line[i]))
data_array.append(line_array)
label_array.append(float(current_line[-1]))
return data_array, label_array

基於單層決策樹構建弱分類器

1、廢話文學一下，stump的意思的樹樁，單層決策樹就是只有一層的決策樹，就是簡單的通過大於和小於根據阈值（threshold）把數據分為兩堆。在阈值一邊的數據被分到類別-1，另一邊分到類別1。

def stump_classify(data_matrix, dimension, threshold, inequality_sign):
# dimension是數據集第dimension維的特征，對應data_matrix的第dimension列
return_array = ones((shape(data_matrix)[0], 1))
if inequality_sign == 'less_than':
return_array[data_matrix[:, dimension] <= threshold] = -1.0
else:
return_array[data_matrix[:, dimension] > threshold] = -1.0
return return_array

2、遍歷上面stump_classify函數所有可能的輸入值，找到最佳的單層決策樹（給定權重向量d時所得到的最佳單層決策樹）。best_stump就是最佳的單層決策樹，一個字典，裡面存放這個單層決策樹的'dimension'（上一段代碼注釋）、'threshold'（阈值）、'inequality_sign'（不等號，less_than和greater_than）。

結合代碼和注釋看即可。

def build_stump(data_array, class_labels, d):
data_matrix = mat(data_array)
label_matrix = mat(class_labels).T
m, n = shape(data_matrix)
num_steps = 10.0
best_stump = {} # 用於存放給定權重向量d時所得到的最佳單層決策樹的相關信息
best_class_estimate = mat(zeros((m, 1)))
'''
將最小錯誤率min_error設為inf
對數據集中的每一個特征（第一層循環）：
對每一個步長（第二層循環）：
對每一個不等號（第三層循環）：
建立一棵單層決策樹並利用加權數據集對它進行測試
如果錯誤率低於min_error，則將當前單層決策樹設為最佳單層決策樹
返回最佳單層決策樹
'''
min_error = inf
for i in range(n):
range_min = data_matrix[:, i].min()
range_max = data_matrix[:, i].max()
step_size = (range_max - range_min) / num_steps
for j in range(-1, int(num_steps) + 1):
for inequality_sign in ['less_than', 'greater_than']:
threshold = (range_min + float(j) * step_size)
predicted_values = stump_classify(data_matrix, i, threshold, inequality_sign) # 調用stump_classify函數來得到預測結果
error_array = mat(ones((m, 1))) # 這是一個與分類預測結果相同長度的列向量，如果predicted_values中的值不等於label_matrix中的標簽值，對應位置就為1，否則為0.
error_array[predicted_values == label_matrix] = 0
weighted_error = d.T * error_array # 這個是加權錯誤率，這個將用來更新權重向量d
if weighted_error < min_error:
min_error = weighted_error
best_class_estimate = predicted_values.copy()
best_stump['dimension'] = i
best_stump['threshold'] = threshold
best_stump['inequality_sign'] = inequality_sign
return best_stump, min_error, best_class_estimate

加權錯誤率weighted_error是與AdaBoost交互的地方，每次用於更新權重向量d.

Adaboost的訓練過程和分類

訓練

訓練出來的返回值是： weak_classifier_array, aggregate_class_estimate，一個存放了很多弱分類器的數組和集成學習的類別估計值。

於是思路是，對於每次迭代：利用build_stump找到最佳的單層決策樹；把這個最佳單層決策樹放進弱分類器數組；利用錯誤率計算弱分類器的權重α；更新權重向量d；更新集成學習的類別估計值；更新錯誤率。

裡面出現的公式：

錯誤率：
利用錯誤率計算弱分類器的權重α：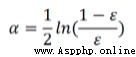

可見錯誤率ε越高，這個分類器的權重就越小。代碼中：

alpha = float(0.5 * log((1.0 - error) / max([error, 1e-16])))

（注：max函數裡面加中括號是因為之前from numpy import *了，這個max是np.amax，不加中括號會有一個warning.）

更新權重向量d：就是使被分錯的樣本在接下來學習中可以重點對其進行學習。

第i個樣本分類正確就是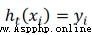
，Zt是sum(D)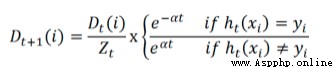

上面公式淺看一下，編程是對著化簡合並後的公式來的：

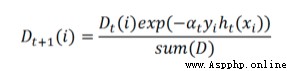
代碼中：

exp的指數：exponent = multiply(-1 * alpha * mat(class_labels).T, class_estimate)

d：d = multiply(d, exp(exponent))和d = d / d.sum()

集成學習的類別估計值（aggregate_class_estimate）就是把每個弱分類器給出的估計值按照每個弱分類器的權重累加起來。代碼中是在一個循環裡：aggregate_class_estimate += alpha * class_estimate

下面直接放代碼應該就很清楚了：

def ada_boost_train_decision_stump(data_array, class_labels, num_iteration=40):
weak_classifier_array = []
m = shape(data_array)[0]
d = mat(ones((m, 1)) / m)
aggregate_class_estimate = mat(zeros((m, 1)))
for i in range(num_iteration):
best_stump, error, class_estimate = build_stump(data_array, class_labels, d) # 利用build_stump找到最佳單層決策樹
alpha = float(0.5 * log((1.0 - error) / max([error, 1e-16]))) # 算α
best_stump['alpha'] = alpha
weak_classifier_array.append(best_stump) # 把這個最佳單層決策樹扔進弱分類器數組
exponent = multiply(-1 * alpha * mat(class_labels).T, class_estimate) # 算d
d = multiply(d, exp(exponent))
d = d / d.sum()
aggregate_class_estimate += alpha * class_estimate # 算集成學習的類別估計值
aggregate_errors = multiply(sign(aggregate_class_estimate) != mat(class_labels).T, ones((m, 1)))
error_rate = aggregate_errors.sum() / m
if error_rate == 0.0: # 如果錯誤率為0了就退出循環
break
return weak_classifier_array, aggregate_class_estimate

分類

就是寫個循環，把上面得到的弱分類器數組裡面每個弱分類器的放進stump_classify函數裡面跑一遍，根據每個的權重把結果累加起來即可。

def ada_boost_classify(data_array, classifier_array):
data_matrix = mat(data_array)
m = shape(data_matrix)[0]
aggregate_class_estimate = mat(zeros((m, 1)))
for i in range(len(classifier_array)):
class_estimate = stump_classify(data_matrix,
classifier_array[i]['dimension'],
classifier_array[i]['threshold'],
classifier_array[i]['inequality_sign'])
aggregate_class_estimate += classifier_array[i]['alpha'] * class_estimate
return sign(aggregate_class_estimate)

以上就是實現過程了。下面再放上比較正規的偽代碼：

完整代碼

from numpy import *
def load_dataset(filename):
num_feature = len(open(filename).readline().split('\t'))
data_array = []
label_array = []
f = open(filename)
for line in f.readlines():
line_array = []
current_line = line.strip().split('\t')
for i in range(num_feature - 1):
line_array.append(float(current_line[i]))
data_array.append(line_array)
label_array.append(float(current_line[-1]))
return data_array, label_array
def stump_classify(data_matrix, dimension, threshold, inequality_sign):
return_array = ones((shape(data_matrix)[0], 1))
if inequality_sign == 'less_than':
return_array[data_matrix[:, dimension] <= threshold] = -1.0
else:
return_array[data_matrix[:, dimension] > threshold] = -1.0
return return_array
def build_stump(data_array, class_labels, d):
data_matrix = mat(data_array)
label_matrix = mat(class_labels).T
m, n = shape(data_matrix)
num_steps = 10.0
best_stump = {}
best_class_estimate = mat(zeros((m, 1)))
min_error = inf
for i in range(n):
range_min = data_matrix[:, i].min()
range_max = data_matrix[:, i].max()
step_size = (range_max - range_min) / num_steps
for j in range(-1, int(num_steps) + 1):
for inequality_sign in ['less_than', 'greater_than']:
threshold = (range_min + float(j) * step_size)
predicted_values = stump_classify(data_matrix, i, threshold, inequality_sign)
error_array = mat(ones((m, 1)))
error_array[predicted_values == label_matrix] = 0
weighted_error = d.T * error_array
if weighted_error < min_error:
min_error = weighted_error
best_class_estimate = predicted_values.copy()
best_stump['dimension'] = i
best_stump['threshold'] = threshold
best_stump['inequality_sign'] = inequality_sign
return best_stump, min_error, best_class_estimate
def ada_boost_train_decision_stump(data_array, class_labels, num_iteration=40):
weak_classifier_array = []
m = shape(data_array)[0]
d = mat(ones((m, 1)) / m)
aggregate_class_estimate = mat(zeros((m, 1)))
for i in range(num_iteration):
best_stump, error, class_estimate = build_stump(data_array, class_labels, d)
alpha = float(0.5 * log((1.0 - error) / max([error, 1e-16])))
best_stump['alpha'] = alpha
weak_classifier_array.append(best_stump)
exponent = multiply(-1 * alpha * mat(class_labels).T, class_estimate)
d = multiply(d, exp(exponent))
d = d / d.sum()
aggregate_class_estimate += alpha * class_estimate
aggregate_errors = multiply(sign(aggregate_class_estimate) != mat(class_labels).T, ones((m, 1)))
error_rate = aggregate_errors.sum() / m
if error_rate == 0.0:
break
return weak_classifier_array, aggregate_class_estimate
def ada_boost_classify(data_array, classifier_array):
data_matrix = mat(data_array)
m = shape(data_matrix)[0]
aggregate_class_estimate = mat(zeros((m, 1)))
for i in range(len(classifier_array)):
class_estimate = stump_classify(data_matrix,
classifier_array[i]['dimension'],
classifier_array[i]['threshold'],
classifier_array[i]['inequality_sign'])
aggregate_class_estimate += classifier_array[i]['alpha'] * class_estimate
return sign(aggregate_class_estimate)
def main():
data_array, label_array = load_dataset('AdaBoost/horseColicTraining2.txt')
weak_classier_array, aggregate_class_estimate = ada_boost_train_decision_stump(data_array, label_array, 40)
test_array, test_label_array = load_dataset('AdaBoost/horseColicTest2.txt')
print(weak_classier_array)
predictions = ada_boost_classify(data_array, weak_classier_array)
error_array = mat(ones((len(data_array), 1)))
print('error rate of training set: %.3f%%'
% float(error_array[predictions != mat(label_array).T].sum() / len(data_array) * 100))
predictions = ada_boost_classify(test_array, weak_classier_array)
error_array = mat(ones((len(test_array), 1)))
print('error rate of test set: %.3f%%'
% float(error_array[predictions != mat(test_label_array).T].sum() / len(test_array) * 100))
if __name__ == '__main__':
main()

輸出是：前面是訓練得到的弱分類器，後面是錯誤率。

[{'dimension': 9, 'threshold': 3.0, 'inequality_sign': 'greater_than', 'alpha': 0.4616623792657674}, {'dimension': 17, 'threshold': 52.5, 'inequality_sign': 'greater_than', 'alpha': 0.31248245042467104}, {'dimension': 3, 'threshold': 55.199999999999996, 'inequality_sign': 'greater_than', 'alpha': 0.2868097320169572}, {'dimension': 18, 'threshold': 62.300000000000004, 'inequality_sign': 'less_than', 'alpha': 0.23297004638939556}, {'dimension': 10, 'threshold': 0.0, 'inequality_sign': 'less_than', 'alpha': 0.19803846151213728}, {'dimension': 5, 'threshold': 2.0, 'inequality_sign': 'greater_than', 'alpha': 0.1884788734902058}, {'dimension': 12, 'threshold': 1.2, 'inequality_sign': 'less_than', 'alpha': 0.1522736899747682}, {'dimension': 7, 'threshold': 1.2, 'inequality_sign': 'greater_than', 'alpha': 0.15510870821690584}, {'dimension': 5, 'threshold': 0.0, 'inequality_sign': 'less_than', 'alpha': 0.1353619735335944}, {'dimension': 4, 'threshold': 28.799999999999997, 'inequality_sign': 'less_than', 'alpha': 0.12521587326132164}, {'dimension': 11, 'threshold': 2.0, 'inequality_sign': 'greater_than', 'alpha': 0.13347648128207715}, {'dimension': 9, 'threshold': 4.0, 'inequality_sign': 'less_than', 'alpha': 0.14182243253771004}, {'dimension': 14, 'threshold': 0.0, 'inequality_sign': 'greater_than', 'alpha': 0.10264268449708018}, {'dimension': 0, 'threshold': 1.0, 'inequality_sign': 'less_than', 'alpha': 0.11883732872109554}, {'dimension': 4, 'threshold': 19.2, 'inequality_sign': 'greater_than', 'alpha': 0.09879216527106725}, {'dimension': 2, 'threshold': 36.72, 'inequality_sign': 'less_than', 'alpha': 0.12029960885056902}, {'dimension': 3, 'threshold': 92.0, 'inequality_sign': 'less_than', 'alpha': 0.10846927663989149}, {'dimension': 15, 'threshold': 0.0, 'inequality_sign': 'less_than', 'alpha': 0.09652967982091365}, {'dimension': 3, 'threshold': 73.6, 'inequality_sign': 'greater_than', 'alpha': 0.08958515309272022}, {'dimension': 18, 'threshold': 8.9, 'inequality_sign': 'less_than', 'alpha': 0.0921036196127237}, {'dimension': 16, 'threshold': 4.0, 'inequality_sign': 'greater_than', 'alpha': 0.10464142217079568}, {'dimension': 11, 'threshold': 3.2, 'inequality_sign': 'less_than', 'alpha': 0.09575457291711578}, {'dimension': 20, 'threshold': 0.0, 'inequality_sign': 'greater_than', 'alpha': 0.09624217440331542}, {'dimension': 17, 'threshold': 37.5, 'inequality_sign': 'less_than', 'alpha': 0.07859662885189661}, {'dimension': 9, 'threshold': 2.0, 'inequality_sign': 'less_than', 'alpha': 0.07142863634550768}, {'dimension': 5, 'threshold': 2.0, 'inequality_sign': 'greater_than', 'alpha': 0.07830753154662261}, {'dimension': 4, 'threshold': 28.799999999999997, 'inequality_sign': 'less_than', 'alpha': 0.07606159074712755}, {'dimension': 4, 'threshold': 19.2, 'inequality_sign': 'greater_than', 'alpha': 0.08306752811081908}, {'dimension': 7, 'threshold': 4.2, 'inequality_sign': 'greater_than', 'alpha': 0.08304167411411778}, {'dimension': 3, 'threshold': 92.0, 'inequality_sign': 'less_than', 'alpha': 0.08893356802801176}, {'dimension': 14, 'threshold': 3.0, 'inequality_sign': 'greater_than', 'alpha': 0.07000509315417822}, {'dimension': 7, 'threshold': 5.3999999999999995, 'inequality_sign': 'less_than', 'alpha': 0.07697582358566012}, {'dimension': 18, 'threshold': 0.0, 'inequality_sign': 'less_than', 'alpha': 0.08507457442866745}, {'dimension': 5, 'threshold': 3.2, 'inequality_sign': 'less_than', 'alpha': 0.06765903873020729}, {'dimension': 7, 'threshold': 3.0, 'inequality_sign': 'greater_than', 'alpha': 0.08045680822237077}, {'dimension': 12, 'threshold': 1.2, 'inequality_sign': 'less_than', 'alpha': 0.05616862921969537}, {'dimension': 11, 'threshold': 2.0, 'inequality_sign': 'greater_than', 'alpha': 0.06454264376249834}, {'dimension': 7, 'threshold': 5.3999999999999995, 'inequality_sign': 'less_than', 'alpha': 0.053088884353829344}, {'dimension': 11, 'threshold': 0.0, 'inequality_sign': 'less_than', 'alpha': 0.07346058614788575}, {'dimension': 13, 'threshold': 0.0, 'inequality_sign': 'greater_than', 'alpha': 0.07872267320907471}]
error rate of training set: 19.732%
error rate of test set: 19.403%