Python Machine learning algorithm implementation
Author:louwill
As a large class of models in machine learning , Tree model has been paid much attention by the academia and the industry . At present, no matter in major competitions, all kinds of big killers XGBoost、lightgbm Or random forest 、Adaboost And other typical ensemble learning models , They are all based on the decision tree model . Traditional decision tree algorithms include ID3 Algorithm 、C4.5 Algorithm and GBDT The base classifier of CART Algorithm .\
The main difference of the three classic decision tree algorithms is the difference of their feature selection criteria .ID3 The basis of feature selection is information gain 、C4.5 It's the information gain ratio , and CART It is Gini Index . As a basic method of classification and regression , Decision trees can be understood in two ways . One is that we can think of a decision tree as a set of if-then Set of rules , The other is the conditional probability distribution of a class under given characteristic conditions . About these two ways of understanding , Readers can read relevant textbooks to understand , The author is here to make up the details .
According to the above two ways of understanding , We can take the essence of decision tree as a set of classification rules from the training data set , It can also be seen as estimating conditional probability models from training data sets . The learning process of the whole decision tree is to select the optimal feature recursively , According to this feature, the data set is divided , The process of making each sample get the best classification .
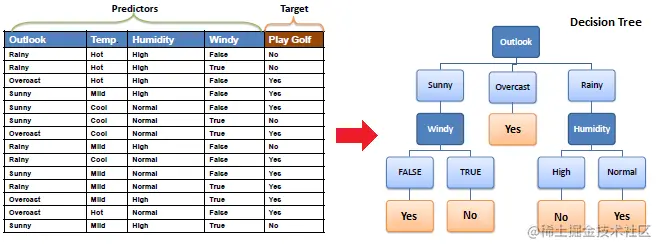
So the key here is how to select the best features to divide the data set . The answer is the information gain mentioned earlier 、 Information gain ratio and Gini Index . Because this article is about ID3 Algorithm , So here the author only gives a detailed description of information gain .
Before we talk about information gain , Here we must first introduce the concept of entropy . In information theory , Entropy is a measure of the uncertainty of random variables . If we scatter random variables X The probability distribution of is :
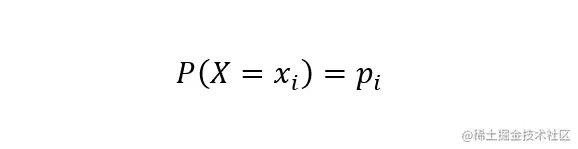 \
\
Then the random variable X Entropy is defined as :
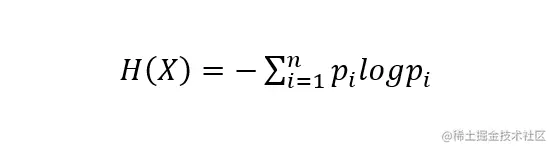
Empathy , For continuous random variables Y, Its entropy can be defined as :
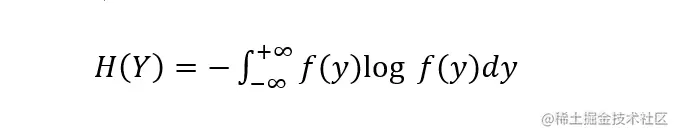
When you give a random variable X Is a random variable Y The entropy of is defined as conditional entropy H(Y|X):
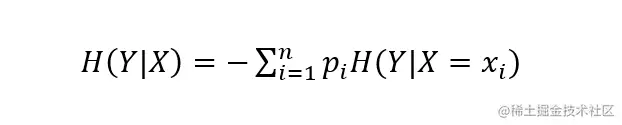
The so-called information gain is that the data is getting characteristics X The information of the class makes the class Y The degree to which information uncertainty is reduced . Hypothetical data set D The entropy of information is H(D), Given characteristics A And then the conditional entropy is H(D|A), Characteristics A For the information gain of the data set g(D,A) Can be expressed as :
g(D,A) = H(D) - H(D|A)
The larger the information gain , The greater the contribution of the feature to the certainty of the dataset , It indicates that the feature has strong classification ability for data . An example of information gain calculation is as follows :
1). Calculate the information entropy of the target features .

2). Calculate the conditional entropy after adding a feature .
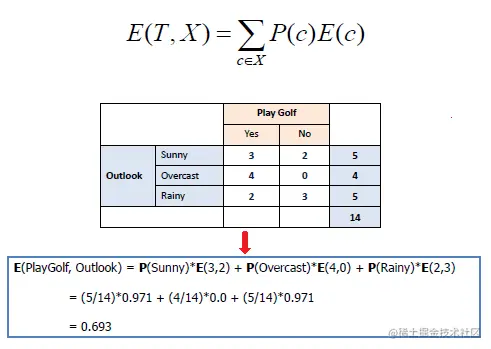
3). Calculated information gain .
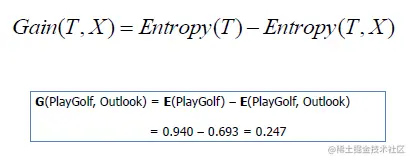
That's all ID3 The core theory of the algorithm , As for how to base on ID3 Construct a decision tree , Let's look at the code example .
ID3 Algorithm implementation \
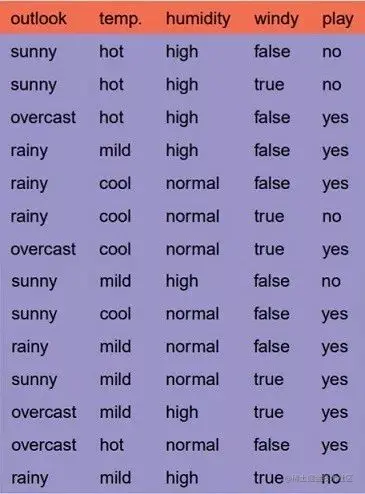
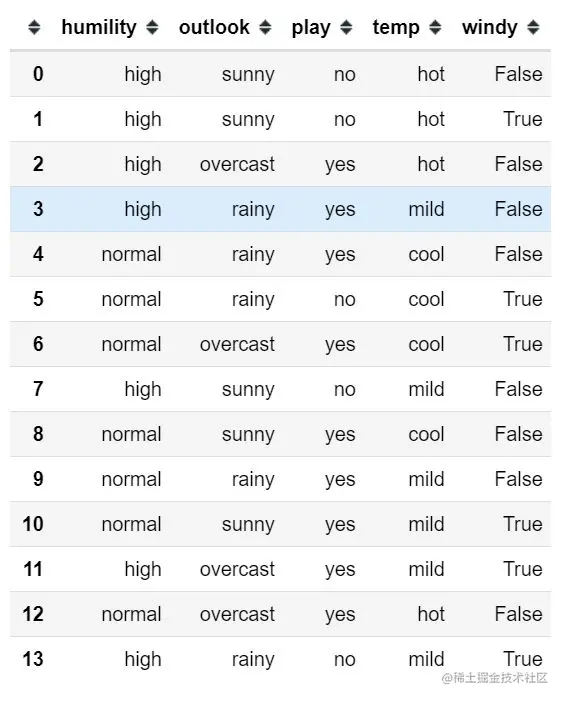
First read in the sample dataset :
import numpy as np
import pandas as pd
from math import log
df = pd.read_csv('./example_data.csv')
df
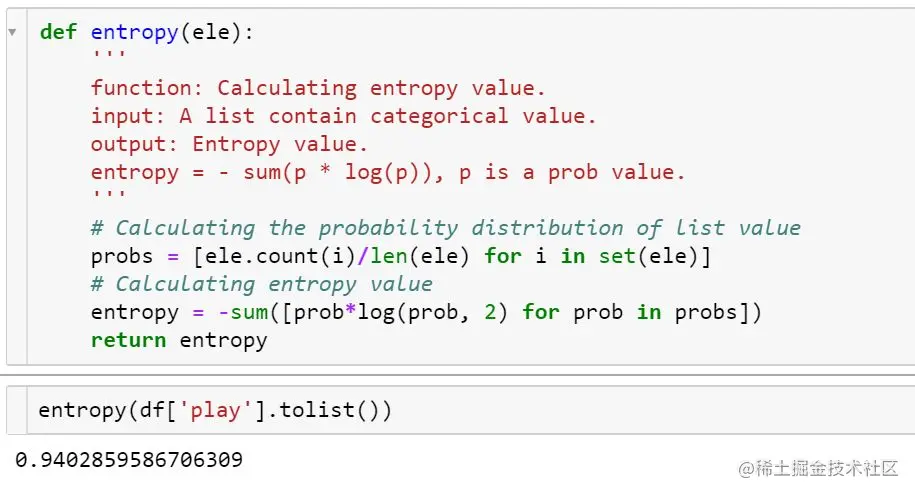
Define the computational function of entropy :\
def entropy(ele):
''' function: Calculating entropy value. input: A list contain categorical value. output: Entropy value. entropy = - sum(p * log(p)), p is a prob value. '''
# Calculating the probability distribution of list value
probs = [ele.count(i)/len(ele) for i in set(ele)]
# Calculating entropy value
entropy = -sum([prob*log(prob, 2) for prob in probs])
return entropy
Calculation example :
 \
\
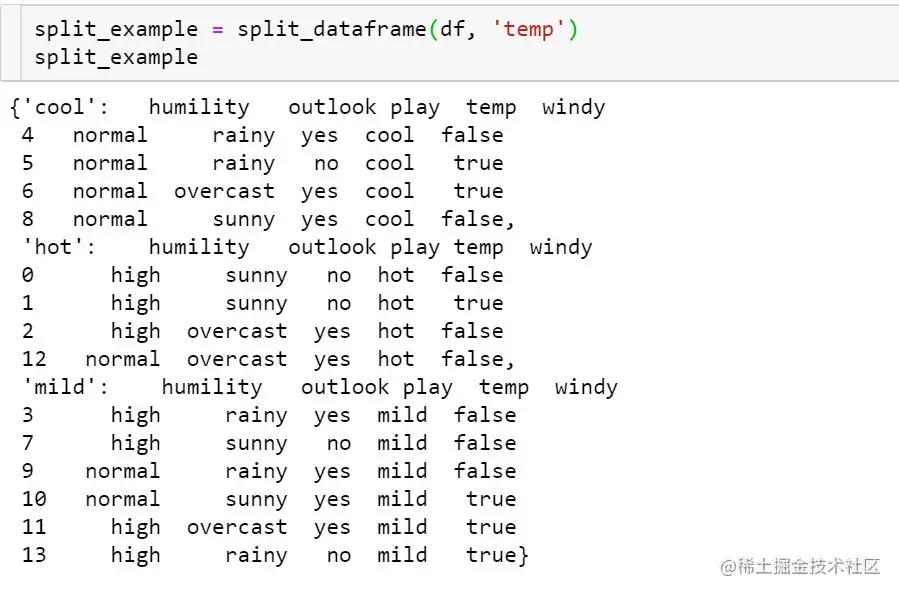
Then we need to define the method of data partition based on characteristics and eigenvalues :
def split_dataframe(data, col):
''' function: split pandas dataframe to sub-df based on data and column. input: dataframe, column name. output: a dict of splited dataframe. '''
# unique value of column
unique_values = data[col].unique()
# empty dict of dataframe
result_dict = {elem : pd.DataFrame for elem in unique_values}
# split dataframe based on column value
for key in result_dict.keys():
result_dict[key] = data[:][data[col] == key]
return result_dict
according to temp And its three eigenvalues of the data set partition example :
Then the information gain is calculated according to the entropy calculation formula and data set partition method to select the best feature :
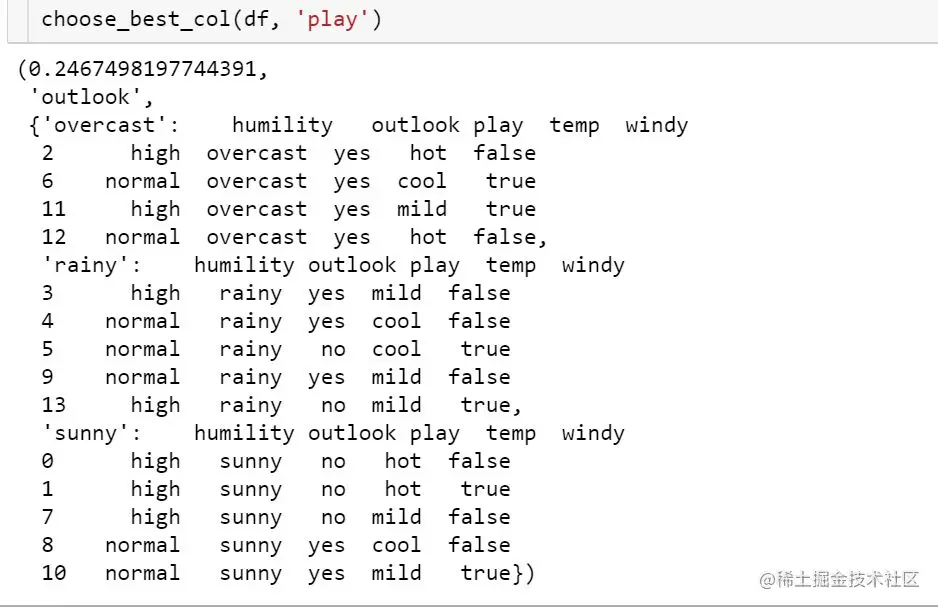
def choose_best_col(df, label):
''' funtion: choose the best column based on infomation gain. input: datafram, label output: max infomation gain, best column, splited dataframe dict based on best column. '''
# Calculating label's entropy entropy_D = entropy(df[label].tolist()) # columns list except label cols = [col for col in df.columns if col not in [label]] # initialize the max infomation gain, best column and best splited dict max_value, best_col = -999, None max_splited = None # split data based on different column for col in cols: splited_set = split_dataframe(df, col) entropy_DA = 0 for subset_col, subset in splited_set.items(): # calculating splited dataframe label's entropy
entropy_Di = entropy(subset[label].tolist())
# calculating entropy of current feature
entropy_DA += len(subset)/len(df) * entropy_Di
# calculating infomation gain of current feature
info_gain = entropy_D - entropy_DA
if info_gain > max_value:
max_value, best_col = info_gain, col
max_splited = splited_set
return max_value, best_col, max_splited
The feature of the first selected information gain is outlook:
After the basic elements of decision tree are defined , We can define one according to the above function ID3 Algorithm class , Define constructs in a class ID3 Decision tree approach :
class ID3Tree:
# define a Node class
class Node:
def __init__(self, name):
self.name = name
self.connections = {}
def connect(self, label, node):
self.connections[label] = node
def __init__(self, data, label):
self.columns = data.columns
self.data = data
self.label = label
self.root = self.Node("Root")
# print tree method
def print_tree(self, node, tabs):
print(tabs + node.name)
for connection, child_node in node.connections.items():
print(tabs + "\t" + "(" + connection + ")")
self.print_tree(child_node, tabs + "\t\t")
def construct_tree(self):
self.construct(self.root, "", self.data, self.columns)
# construct tree
def construct(self, parent_node, parent_connection_label, input_data, columns):
max_value, best_col, max_splited = choose_best_col(input_data[columns], self.label)
if not best_col:
node = self.Node(input_data[self.label].iloc[0])
parent_node.connect(parent_connection_label, node)
return
node = self.Node(best_col)
parent_node.connect(parent_connection_label, node)
new_columns = [col for col in columns if col != best_col]
# Recursively constructing decision trees
for splited_value, splited_data in max_splited.items():
self.construct(node, splited_value, splited_data, new_columns)
Based on the above code and the sample dataset, construct a ID3 Decision tree :
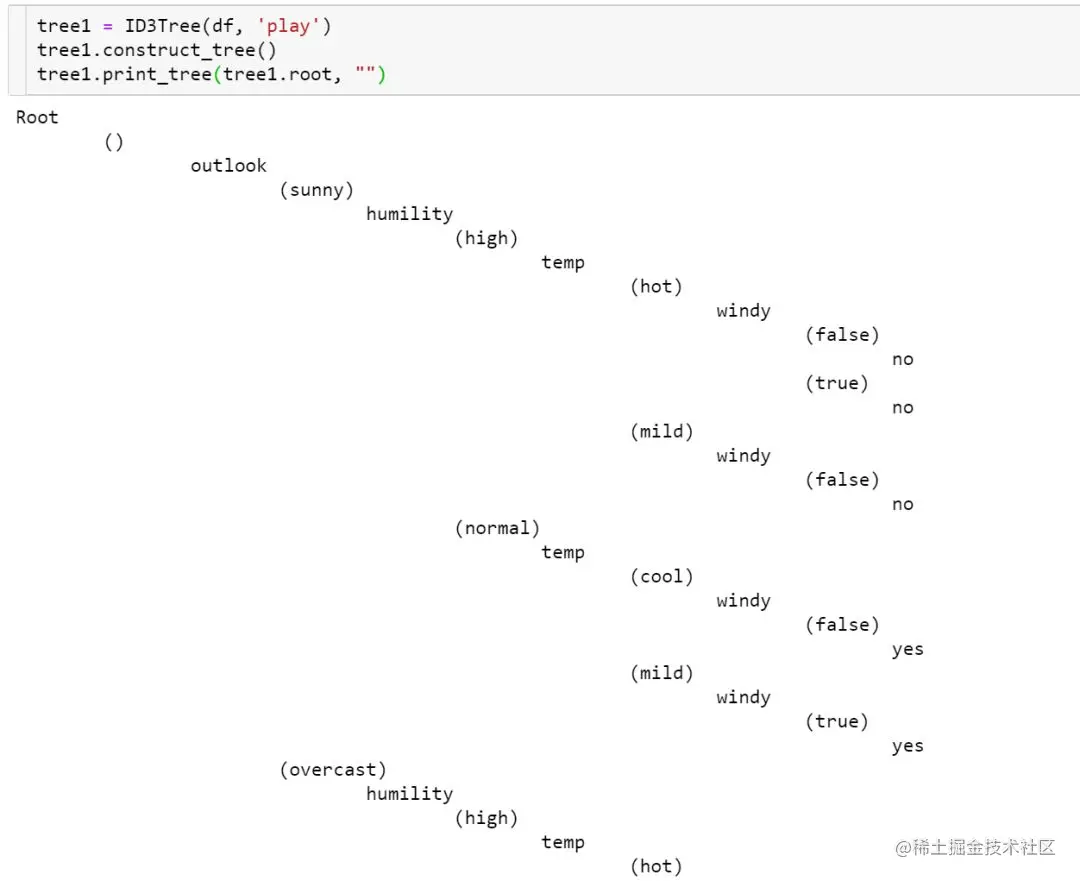
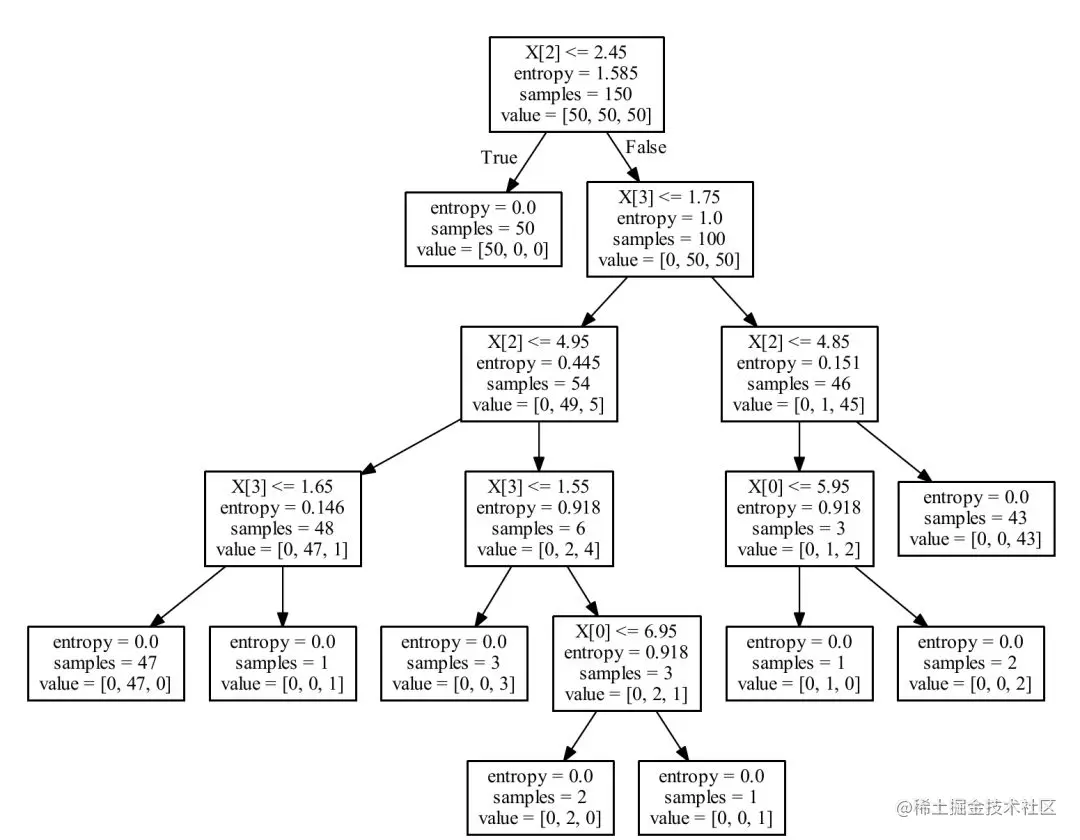
The above is ID3 The handwritten process of the algorithm .sklearn in tree Module provides us with the implementation of decision tree , The reference codes are as follows :
from sklearn.datasets import load_iris
from sklearn import tree
import graphviz
iris = load_iris()
# criterion choice entropy, Here is the choice ID3 Algorithm
clf = tree.DecisionTreeClassifier(criterion='entropy', splitter='best')
clf = clf.fit(iris.data, iris.target)
dot_data = tree.export_graphviz(clf, out_file=None,
feature_names=iris.feature_names,
class_names=iris.target_names,
filled=True,
rounded=True,
special_characters=True)
graph = graphviz.Source(dot_data)
graph
Past highlights :
Mathematical derivation + pure Python Implement machine learning algorithms 3:k a near neighbor **
**
Mathematical derivation + pure Python Implement machine learning algorithms 2: Logical regression **
**
Mathematical derivation + pure Python Implement machine learning algorithms 1: Linear regression