Here, I'll sort out the realization of the experimental class A weak classifier based on single-layer decision tree Of AdaBoost Algorithm .
Because I'm a beginner , When looking for materials in the experiment class, I saw too many English abbreviations in other people's code , It's not easy to understand , But also look at the details of the code implementation 、 The principle of the algorithm , The experience was very bad .
So there is no abbreviation in the code here , Try to write your thoughts clearly .
Integrated learning : By combining multiple base classifiers (base classifier) To complete the learning task , Base classifiers generally use weak learners .
Weak learner : Only learning accuracy is only slightly better than random guessing . Through an integrated approach , Can be combined into a strong learner .
Bagging and Boosting: There are two main methods of ensemble learning to assemble weak classifiers into strong classifiers .
AdaBoost yes adaptive boosting Abbreviation .
Bagging: The training set is extracted from the original data set , Each training set is independent . One model at a time using one training set . The classification problem makes these models vote to get the classification results , The regression problem is the mean of these models .
Boosting: The training set of each round is the same , It's just that the weight of each sample in the training set changes in the classifier , And the weight distribution of samples in each round depends on the classification results of the previous round . Each weak classifier also has its own weight , The classifier with small classification error has greater weight .
for instance :Bagging+ Decision tree = Random forests ;Boosting+ Decision tree = Ascension tree
AdaBoost: Calculate the sample weight -> Calculate the error rate -> Calculate the weight of the weak learner -> Update sample weight ... repeat .
Is to construct a weak classifier , And then assembled according to certain methods .
from numpy import *
The data set given in the experiment class is used (horseColic Equine hernia data set )... I won't say much about this part . belt _array The suffix is a list , belt _matrix The suffix is the corresponding array Become np matrix .
def load_dataset(filename):
num_feature = len(open(filename).readline().split('\t'))
data_array = []
label_array = []
f = open(filename)
for line in f.readlines():
line_array = []
current_line = line.strip().split('\t')
for i in range(num_feature - 1):
line_array.append(float(current_line[i]))
data_array.append(line_array)
label_array.append(float(current_line[-1]))
return data_array, label_array
1、 Nonsense Literature ,stump A tree stump , A single-layer decision tree is a decision tree with only one layer , That is, simply by being greater than or less than the threshold (threshold) Divide the data into two piles . The data on the threshold side is classified into categories -1, The other side is divided into categories 1.
def stump_classify(data_matrix, dimension, threshold, inequality_sign):
# dimension It's data set number two dimension Dimension characteristics , Corresponding data_matrix Of the dimension Column
return_array = ones((shape(data_matrix)[0], 1))
if inequality_sign == 'less_than':
return_array[data_matrix[:, dimension] <= threshold] = -1.0
else:
return_array[data_matrix[:, dimension] > threshold] = -1.0
return return_array
2、 Traverse above stump_classify Function all possible input values , Find the best single-layer decision tree ( Given the weight vector d The best single-layer decision tree ).best_stump Is the best single-layer decision tree , A dictionary , Which stores the single-layer decision tree 'dimension'( The last code comment )、'threshold'( threshold )、'inequality_sign'( Unequal sign ,less_than and greater_than).
Combine the code and comments .
def build_stump(data_array, class_labels, d):
data_matrix = mat(data_array)
label_matrix = mat(class_labels).T
m, n = shape(data_matrix)
num_steps = 10.0
best_stump = {} # Used to store the given weight vector d The relevant information of the best single-layer decision tree
best_class_estimate = mat(zeros((m, 1)))
'''
The minimum error rate min_error Set to inf
For every feature in the dataset ( Layer 1 cycle ):
For each step ( The second cycle ):
For every inequality sign ( The third cycle ):
Build a single-layer decision tree and test it with weighted data set
If the error rate is lower than min_error, Then set the current single-layer decision tree as the best single-layer decision tree
Return to the best single-layer decision tree
'''
min_error = inf
for i in range(n):
range_min = data_matrix[:, i].min()
range_max = data_matrix[:, i].max()
step_size = (range_max - range_min) / num_steps
for j in range(-1, int(num_steps) + 1):
for inequality_sign in ['less_than', 'greater_than']:
threshold = (range_min + float(j) * step_size)
predicted_values = stump_classify(data_matrix, i, threshold, inequality_sign) # call stump_classify Function to get the predicted result
error_array = mat(ones((m, 1))) # This is a column vector with the same length as the classification prediction result , If predicted_values The value in is not equal to label_matrix Tag value in , The corresponding position is 1, Otherwise 0.
error_array[predicted_values == label_matrix] = 0
weighted_error = d.T * error_array # This is the weighted error rate , This will be used to update the weight vector d
if weighted_error < min_error:
min_error = weighted_error
best_class_estimate = predicted_values.copy()
best_stump['dimension'] = i
best_stump['threshold'] = threshold
best_stump['inequality_sign'] = inequality_sign
return best_stump, min_error, best_class_estimate
Weighted error rate weighted_error Is with the AdaBoost The place of interaction , Each time it is used to update the weight vector d.
The return value of the training is : weak_classifier_array, aggregate_class_estimate, An array storing many weak classifiers and the class estimate of ensemble learning .
So the idea is , For each iteration : utilize build_stump Find the best single-layer decision tree ; Put the best single-layer decision tree into the weak classifier array ; Using the error rate to calculate the weight of the weak classifier α; Update weight vector d; Update category estimates for integrated learning ; Update error rate .
The formula that appears inside :
Error rate :
Using the error rate to calculate the weight of the weak classifier α: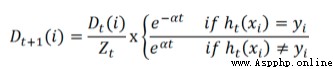
Visible error rate ε The higher the , The smaller the weight of this classifier . In the code :
alpha = float(0.5 * log((1.0 - error) / max([error, 1e-16])))
( notes :max The parentheses are added to the function because before from numpy import * 了 , This max yes np.amax, Without brackets, there will be a warning.)
The first i The correct classification of samples is 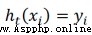
,Zt yes sum(D)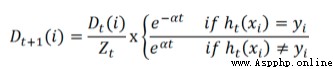
Let's take a look at the above formula , Programming is aimed at simplifying the merged formula :
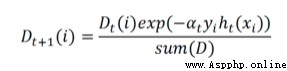
In the code :
exp The index of :exponent = multiply(-1 * alpha * mat(class_labels).T, class_estimate)
d:d = multiply(d, exp(exponent)) and d = d / d.sum()
aggregate_class_estimate += alpha * class_estimateIt should be clear to put the code directly below :
def ada_boost_train_decision_stump(data_array, class_labels, num_iteration=40):
weak_classifier_array = []
m = shape(data_array)[0]
d = mat(ones((m, 1)) / m)
aggregate_class_estimate = mat(zeros((m, 1)))
for i in range(num_iteration):
best_stump, error, class_estimate = build_stump(data_array, class_labels, d) # utilize build_stump Find the best single-layer decision tree
alpha = float(0.5 * log((1.0 - error) / max([error, 1e-16]))) # count α
best_stump['alpha'] = alpha
weak_classifier_array.append(best_stump) # Throw the best single-layer decision tree into the weak classifier array
exponent = multiply(-1 * alpha * mat(class_labels).T, class_estimate) # count d
d = multiply(d, exp(exponent))
d = d / d.sum()
aggregate_class_estimate += alpha * class_estimate # Calculate category estimates for ensemble learning
aggregate_errors = multiply(sign(aggregate_class_estimate) != mat(class_labels).T, ones((m, 1)))
error_rate = aggregate_errors.sum() / m
if error_rate == 0.0: # If the error rate is 0 Exit the loop
break
return weak_classifier_array, aggregate_class_estimate
Just write a loop , Put the weak classifier array obtained above Each weak classifier in it is put into stump_classify Run through the function , Add up the results according to the weight of each .
def ada_boost_classify(data_array, classifier_array):
data_matrix = mat(data_array)
m = shape(data_matrix)[0]
aggregate_class_estimate = mat(zeros((m, 1)))
for i in range(len(classifier_array)):
class_estimate = stump_classify(data_matrix,
classifier_array[i]['dimension'],
classifier_array[i]['threshold'],
classifier_array[i]['inequality_sign'])
aggregate_class_estimate += classifier_array[i]['alpha'] * class_estimate
return sign(aggregate_class_estimate)
The above is the implementation process . Next, put more regular pseudo code :

from numpy import *
def load_dataset(filename):
num_feature = len(open(filename).readline().split('\t'))
data_array = []
label_array = []
f = open(filename)
for line in f.readlines():
line_array = []
current_line = line.strip().split('\t')
for i in range(num_feature - 1):
line_array.append(float(current_line[i]))
data_array.append(line_array)
label_array.append(float(current_line[-1]))
return data_array, label_array
def stump_classify(data_matrix, dimension, threshold, inequality_sign):
return_array = ones((shape(data_matrix)[0], 1))
if inequality_sign == 'less_than':
return_array[data_matrix[:, dimension] <= threshold] = -1.0
else:
return_array[data_matrix[:, dimension] > threshold] = -1.0
return return_array
def build_stump(data_array, class_labels, d):
data_matrix = mat(data_array)
label_matrix = mat(class_labels).T
m, n = shape(data_matrix)
num_steps = 10.0
best_stump = {}
best_class_estimate = mat(zeros((m, 1)))
min_error = inf
for i in range(n):
range_min = data_matrix[:, i].min()
range_max = data_matrix[:, i].max()
step_size = (range_max - range_min) / num_steps
for j in range(-1, int(num_steps) + 1):
for inequality_sign in ['less_than', 'greater_than']:
threshold = (range_min + float(j) * step_size)
predicted_values = stump_classify(data_matrix, i, threshold, inequality_sign)
error_array = mat(ones((m, 1)))
error_array[predicted_values == label_matrix] = 0
weighted_error = d.T * error_array
if weighted_error < min_error:
min_error = weighted_error
best_class_estimate = predicted_values.copy()
best_stump['dimension'] = i
best_stump['threshold'] = threshold
best_stump['inequality_sign'] = inequality_sign
return best_stump, min_error, best_class_estimate
def ada_boost_train_decision_stump(data_array, class_labels, num_iteration=40):
weak_classifier_array = []
m = shape(data_array)[0]
d = mat(ones((m, 1)) / m)
aggregate_class_estimate = mat(zeros((m, 1)))
for i in range(num_iteration):
best_stump, error, class_estimate = build_stump(data_array, class_labels, d)
alpha = float(0.5 * log((1.0 - error) / max([error, 1e-16])))
best_stump['alpha'] = alpha
weak_classifier_array.append(best_stump)
exponent = multiply(-1 * alpha * mat(class_labels).T, class_estimate)
d = multiply(d, exp(exponent))
d = d / d.sum()
aggregate_class_estimate += alpha * class_estimate
aggregate_errors = multiply(sign(aggregate_class_estimate) != mat(class_labels).T, ones((m, 1)))
error_rate = aggregate_errors.sum() / m
if error_rate == 0.0:
break
return weak_classifier_array, aggregate_class_estimate
def ada_boost_classify(data_array, classifier_array):
data_matrix = mat(data_array)
m = shape(data_matrix)[0]
aggregate_class_estimate = mat(zeros((m, 1)))
for i in range(len(classifier_array)):
class_estimate = stump_classify(data_matrix,
classifier_array[i]['dimension'],
classifier_array[i]['threshold'],
classifier_array[i]['inequality_sign'])
aggregate_class_estimate += classifier_array[i]['alpha'] * class_estimate
return sign(aggregate_class_estimate)
def main():
data_array, label_array = load_dataset('AdaBoost/horseColicTraining2.txt')
weak_classier_array, aggregate_class_estimate = ada_boost_train_decision_stump(data_array, label_array, 40)
test_array, test_label_array = load_dataset('AdaBoost/horseColicTest2.txt')
print(weak_classier_array)
predictions = ada_boost_classify(data_array, weak_classier_array)
error_array = mat(ones((len(data_array), 1)))
print('error rate of training set: %.3f%%'
% float(error_array[predictions != mat(label_array).T].sum() / len(data_array) * 100))
predictions = ada_boost_classify(test_array, weak_classier_array)
error_array = mat(ones((len(test_array), 1)))
print('error rate of test set: %.3f%%'
% float(error_array[predictions != mat(test_label_array).T].sum() / len(test_array) * 100))
if __name__ == '__main__':
main()
The output is : The previous is the trained weak classifier , Then there is the error rate .
[{'dimension': 9, 'threshold': 3.0, 'inequality_sign': 'greater_than', 'alpha': 0.4616623792657674}, {'dimension': 17, 'threshold': 52.5, 'inequality_sign': 'greater_than', 'alpha': 0.31248245042467104}, {'dimension': 3, 'threshold': 55.199999999999996, 'inequality_sign': 'greater_than', 'alpha': 0.2868097320169572}, {'dimension': 18, 'threshold': 62.300000000000004, 'inequality_sign': 'less_than', 'alpha': 0.23297004638939556}, {'dimension': 10, 'threshold': 0.0, 'inequality_sign': 'less_than', 'alpha': 0.19803846151213728}, {'dimension': 5, 'threshold': 2.0, 'inequality_sign': 'greater_than', 'alpha': 0.1884788734902058}, {'dimension': 12, 'threshold': 1.2, 'inequality_sign': 'less_than', 'alpha': 0.1522736899747682}, {'dimension': 7, 'threshold': 1.2, 'inequality_sign': 'greater_than', 'alpha': 0.15510870821690584}, {'dimension': 5, 'threshold': 0.0, 'inequality_sign': 'less_than', 'alpha': 0.1353619735335944}, {'dimension': 4, 'threshold': 28.799999999999997, 'inequality_sign': 'less_than', 'alpha': 0.12521587326132164}, {'dimension': 11, 'threshold': 2.0, 'inequality_sign': 'greater_than', 'alpha': 0.13347648128207715}, {'dimension': 9, 'threshold': 4.0, 'inequality_sign': 'less_than', 'alpha': 0.14182243253771004}, {'dimension': 14, 'threshold': 0.0, 'inequality_sign': 'greater_than', 'alpha': 0.10264268449708018}, {'dimension': 0, 'threshold': 1.0, 'inequality_sign': 'less_than', 'alpha': 0.11883732872109554}, {'dimension': 4, 'threshold': 19.2, 'inequality_sign': 'greater_than', 'alpha': 0.09879216527106725}, {'dimension': 2, 'threshold': 36.72, 'inequality_sign': 'less_than', 'alpha': 0.12029960885056902}, {'dimension': 3, 'threshold': 92.0, 'inequality_sign': 'less_than', 'alpha': 0.10846927663989149}, {'dimension': 15, 'threshold': 0.0, 'inequality_sign': 'less_than', 'alpha': 0.09652967982091365}, {'dimension': 3, 'threshold': 73.6, 'inequality_sign': 'greater_than', 'alpha': 0.08958515309272022}, {'dimension': 18, 'threshold': 8.9, 'inequality_sign': 'less_than', 'alpha': 0.0921036196127237}, {'dimension': 16, 'threshold': 4.0, 'inequality_sign': 'greater_than', 'alpha': 0.10464142217079568}, {'dimension': 11, 'threshold': 3.2, 'inequality_sign': 'less_than', 'alpha': 0.09575457291711578}, {'dimension': 20, 'threshold': 0.0, 'inequality_sign': 'greater_than', 'alpha': 0.09624217440331542}, {'dimension': 17, 'threshold': 37.5, 'inequality_sign': 'less_than', 'alpha': 0.07859662885189661}, {'dimension': 9, 'threshold': 2.0, 'inequality_sign': 'less_than', 'alpha': 0.07142863634550768}, {'dimension': 5, 'threshold': 2.0, 'inequality_sign': 'greater_than', 'alpha': 0.07830753154662261}, {'dimension': 4, 'threshold': 28.799999999999997, 'inequality_sign': 'less_than', 'alpha': 0.07606159074712755}, {'dimension': 4, 'threshold': 19.2, 'inequality_sign': 'greater_than', 'alpha': 0.08306752811081908}, {'dimension': 7, 'threshold': 4.2, 'inequality_sign': 'greater_than', 'alpha': 0.08304167411411778}, {'dimension': 3, 'threshold': 92.0, 'inequality_sign': 'less_than', 'alpha': 0.08893356802801176}, {'dimension': 14, 'threshold': 3.0, 'inequality_sign': 'greater_than', 'alpha': 0.07000509315417822}, {'dimension': 7, 'threshold': 5.3999999999999995, 'inequality_sign': 'less_than', 'alpha': 0.07697582358566012}, {'dimension': 18, 'threshold': 0.0, 'inequality_sign': 'less_than', 'alpha': 0.08507457442866745}, {'dimension': 5, 'threshold': 3.2, 'inequality_sign': 'less_than', 'alpha': 0.06765903873020729}, {'dimension': 7, 'threshold': 3.0, 'inequality_sign': 'greater_than', 'alpha': 0.08045680822237077}, {'dimension': 12, 'threshold': 1.2, 'inequality_sign': 'less_than', 'alpha': 0.05616862921969537}, {'dimension': 11, 'threshold': 2.0, 'inequality_sign': 'greater_than', 'alpha': 0.06454264376249834}, {'dimension': 7, 'threshold': 5.3999999999999995, 'inequality_sign': 'less_than', 'alpha': 0.053088884353829344}, {'dimension': 11, 'threshold': 0.0, 'inequality_sign': 'less_than', 'alpha': 0.07346058614788575}, {'dimension': 13, 'threshold': 0.0, 'inequality_sign': 'greater_than', 'alpha': 0.07872267320907471}]
error rate of training set: 19.732%
error rate of test set: 19.403%