C++、Python、MATLAB的除法取余方法總結對比。
既然本文的研究對象是余數,那麼顯然是兩個整數之間的除法,這才是我們主要的運用場景,這一點大家要明白。當然從文中我們也可以看出,Python內置函數divmod()是支持浮點數取余運算的,MATLAB的函數mod()和rem()也是支持浮點數的取余運算的。
在C++中有兩種方法實現整數除法的取余。
一是用取余運算符 % 來實現整數除法的取余;
二是用標准庫math中的函數fmod實現。
下面分別介紹:
方法一:用取余運算符 % 來實現整數除法的取余。
示例代碼如下:
#include <iostream>
using namespace std;
int main()
{
//被除數和除數都為正數的情況
int a1 = 13, b1 = 5;
int c1;
c1 = a1%b1;
cout << "c1的值為:" << c1 << endl;
//被除數和除數都為負數的情況
int a2 = -14, b2 = -5;
int c2;
c2 = a2%b2;
cout << "c2的值為:" << c2 << endl;
//被除數為正數,除數為負數的情況
int a3 = 14, b3 = -5;
int c3;
c3 = a3%b3;
cout << "c3的值為:" << c3 << endl;
//被除數為負數,除數為正數的情況
int a4 = -14, b4 = 5;
int c4;
c4 = a4%b4;
cout << "c4的值為:" << c4 << endl;
return 0;
}
運行結果如下: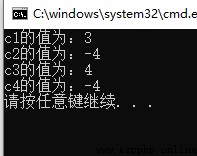
方法二:用標准庫math中的函數fmod()實現
fmod()的原型如下:
double fmod(double X, double Y);
示例代碼如下:
#include <iostream>
#include <math.h>
using namespace std;
int main()
{
double x1 = 9, y1 = 5;
double z1;
z1 = fmod(x1, y1);
cout << "z1的值為:" << z1 << endl;
double x2 = -9, y2 = -5;
double z2;
z2 = fmod(x2, y2);
cout << "z2的值為:" << z2 << endl;
double x3 = -9, y3 = 5;
double z3;
z3 = fmod(x3, y3);
cout << "z3的值為:" << z3 << endl;
double x4 = 9, y4 = -5;
double z4;
z4 = fmod(x4, y4);
cout << "z4的值為:" << z4 << endl;
double x5 = 9, y5 = 5.1;
double z5;
z5 = fmod(x5, y5);
cout << "z5的值為:" << z5 << endl;
double x6 = 9.2, y6 = 5.1;
double z6;
z6 = fmod(x6, y6);
cout << "z6的值為:" << z6 << endl;
double x7 = 9.3, y7 = 5;
double z7;
z7 = fmod(x7, y7);
cout << "z7的值為:" << z7 << endl;
return 0;
}
運行結果如下: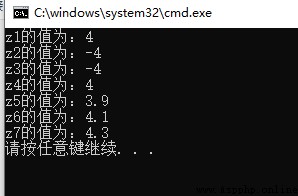
從上面的運行結果可以看出,函數fmod()的余數結果是與被除數相同的,所以它應該與MATLAB中的函數rem()的運算是一樣的。
關於這個操作,這個目前博主沒有發現相關函數,似乎只能讓每個元素與每個元素單獨作取余運算。
或者也可以將矩陣運算的真除結果與向下取整的結果相減實現。
Python中的除法取余運算有兩種,一種是用運算符%實現,另一種是用內置函數divmod()實現,下面分別舉例。
第一種:用運算符%實現
# 被除數和除數都是正數的情況
a1 = 13
b1 = 5
c1 = a1 % b1
# 被除數和除數都是負數的情況
a2 = -14
b2 = -5
c2 = a2 % b2
# 被除數是正數,除數是負數的情況
a3 = 14
b3 = -5
c3 = a3 % b3
# 被除數是負數,除數是正數的情況
a4 = -14
b4 = 5
c4 = a4 % b4
# 驗證被除數是正數,除數是負數時,結果是否為-1
a5 = 23
b5 = -6
c5 = a5 % b5
# 驗證被除數是負數,除數是正數時,結果是否為+1
a6 = -23
b6 = 6
c6 = a6 % b6
# 驗證被除數是正數,除數是負數且能整除時,結果是否為0
a7 = -24
b7 = 6
c7 = a7 % b7
# 驗證被除數是負數,除數是正數且能整除時,結果是否為0
a8 = -24
b8 = 6
c8 = a8 % b8
運算結果如下: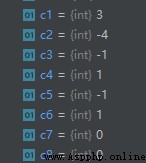
從上面的運算結果可以看出:
那麼,我們可以總結出,實際上余數的符號和除數的符號相同。
第二種:用內置函數divmod()實現
函數divmod()的語法如下:
divmod(a, b)
如果參數 a 與 參數 b 都是整數,函數返回的結果相當於 (a // b, a % b)。
如果其中一個參數為浮點數時,函數返回的結果相當於 (q, a % b),q 通常是 math.floor(a / b),函數會使 q * b + a % b近可能接近於a。
余數的符號與除數相同。
注意:當被除數和除數是異號的整數時,余數只有三個值,當能整除時,余數為0;當不能整除時,若除數為負數,余數為-1,若除數為正數,余數為1。
示例代碼如下:
# 被除數和除數都是正數的情況
a1 = 13
b1 = 5
c01 = divmod(a1, b1)
# 被除數和除數都是負數的情況
a2 = -14
b2 = -5
c02 = divmod(a2, b2)
# 被除數是正數,除數是負數的情況
a3 = 14
b3 = -5
c03 = divmod(a3, b3)
# 被除數是負數,除數是正數的情況
a4 = -14
b4 = 5
c04 = divmod(a4, b4)
# 驗證被除數是正數,除數是負數時,結果是否為-1
a5 = 23
b5 = -6
c05 = divmod(a5, b5)
# 驗證被除數是負數,除數是正數時,結果是否為+1
a6 = -23
b6 = 6
c06 = divmod(a6, b6)
# 驗證被除數是正數,除數是負數且能整除時,結果是否為0
a7 = -24
b7 = 6
c07 = divmod(a7, b7)
# 驗證被除數是負數,除數是正數且能整除時,結果是否為0
a8 = -24
b8 = 6
c08 = divmod(a8, b8)
# 被除數是正的浮點數,除數是正的整數的情況
a9 = 5.3
b9 = 2
c09 = divmod(a9, b9)
# 被除數是負的浮點數,除數是負的整數的情況
a10 = -5.3
b10 = -2
c10 = divmod(a10, b10)
# 被除數是負的浮點數,除數是正的整數的情況
a11 = -5.3
b11 = 2
c11 = divmod(a11, b11)
# 被除數是正的浮點數,除數是負的整數的情況
a12 = 5.3
b12 = -2
c12 = divmod(a12, b12)
# 被除數是整數,除數是浮點數的情況
a13 = 6
b13 = -2.2
c13 = divmod(a13, b13)
# 被除數是浮點數,除數也是浮點數的情況
a14 = 6.8
b14 = -2.2
c14 = divmod(a14, b14)
運行結果如下: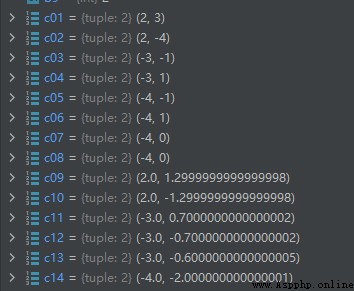
Numpy庫中的ndarray對象的取余運算有三種方法,詳情見博文https://blog.csdn.net/wenhao_ir/article/details/125226556的第10點。
在MATLAB中可以用函數mod()和rem()實現除法的取余運算。
二者的語法是一樣的,都是第一個參數為被除數,第二個參數為除數。
語法分別如下:
b = mod(a,m)
r = rem(a,b)
函數mod()和rem()的區別:
二者的主要區別在於計數余數的表達式不一樣:
函數mod()計算余數的表達式為: b = a - m.*floor(a./m),函數floor()為朝負無窮方向的四捨五入,函數floor()的詳情可參考鏈接:https://ww2.mathworks.cn/help/releases/R2019b/matlab/ref/floor.html
函數rem()計算余數的表達式為:r = a - b.*fix(a./b),函數fix()為朝坐標軸零點的四捨五入,函數fix()詳情可參考鏈接:https://ww2.mathworks.cn/help/releases/R2019b/matlab/ref/fix.html
由以上計算式可以生成這樣的結果:mod 函數生成一個為零或與除數具有相同符號的結果。rem 函數生成一個為零或與被除數具有相同符號的結果。問:為什麼會有這樣的結果,你根據函數floor()和函數fix()的定義再帶入實際的例子就明白了。
另一個差別是當除數為零時的約定。mod 函數遵從 mod(a,0) 返回 a 的約定,而 rem 函數遵從 rem(a,0) 返回 NaN 的約定。
兩個結果都有其各自的用途。例如,在進行信號處理時,mod 函數可在周期信號上下文中使用,因為其輸出是周期性的(周期等於除數,而mod的取余結果的符號與除數相同)。
示例代碼如下:
a1 = mod(9,4);
a2 = rem(9,4);
b1 = mod(-9,4);
b2 = rem(-9,4);
c1 = mod(-9.3,4)
c2 = mod(-9.3,4)
運行結果如下: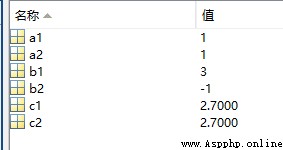
由以上結果可以看出,當被除數為除數都是正數時,兩個函數的結果是一樣的,但是當被除數和除數符號不一樣時,結果就因計算過程中捨入方式的不同而呈現不同的結果了。