C++、Python、MATLAB The methods of division and remainder of .
Since the object of this paper is remainder , So it's obviously the division between two integers , This is our main application scenario , We should understand this . Of course, we can also see from the text ,Python Built in functions divmod() It supports floating-point remainder operation ,MATLAB Function of mod() and rem() It also supports the remainder operation of floating-point numbers .
stay C++ There are two ways to achieve integer division remainder .
One is to use the remainder operator % To achieve integer division remainder ;
The second is to use the standard library math The function in fmod Realization .
Here are the introduction :
Method 1 : Using the remainder operator % To achieve integer division remainder .
The sample code is as follows :
#include <iostream>
using namespace std;
int main()
{
// The case where both the dividend and the divisor are positive
int a1 = 13, b1 = 5;
int c1;
c1 = a1%b1;
cout << "c1 The value of is :" << c1 << endl;
// The case where both the dividend and the divisor are negative
int a2 = -14, b2 = -5;
int c2;
c2 = a2%b2;
cout << "c2 The value of is :" << c2 << endl;
// Divisor is positive , When the divisor is negative
int a3 = 14, b3 = -5;
int c3;
c3 = a3%b3;
cout << "c3 The value of is :" << c3 << endl;
// The divisor is negative , When the divisor is positive
int a4 = -14, b4 = 5;
int c4;
c4 = a4%b4;
cout << "c4 The value of is :" << c4 << endl;
return 0;
}
The operation results are as follows :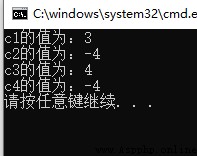
Method 2 : Use standard library math The function in fmod() Realization
fmod() The prototype is as follows :
double fmod(double X, double Y);
The sample code is as follows :
#include <iostream>
#include <math.h>
using namespace std;
int main()
{
double x1 = 9, y1 = 5;
double z1;
z1 = fmod(x1, y1);
cout << "z1 The value of is :" << z1 << endl;
double x2 = -9, y2 = -5;
double z2;
z2 = fmod(x2, y2);
cout << "z2 The value of is :" << z2 << endl;
double x3 = -9, y3 = 5;
double z3;
z3 = fmod(x3, y3);
cout << "z3 The value of is :" << z3 << endl;
double x4 = 9, y4 = -5;
double z4;
z4 = fmod(x4, y4);
cout << "z4 The value of is :" << z4 << endl;
double x5 = 9, y5 = 5.1;
double z5;
z5 = fmod(x5, y5);
cout << "z5 The value of is :" << z5 << endl;
double x6 = 9.2, y6 = 5.1;
double z6;
z6 = fmod(x6, y6);
cout << "z6 The value of is :" << z6 << endl;
double x7 = 9.3, y7 = 5;
double z7;
z7 = fmod(x7, y7);
cout << "z7 The value of is :" << z7 << endl;
return 0;
}
The operation results are as follows :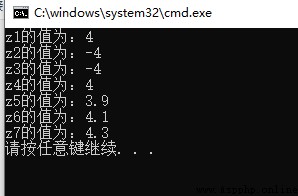
From the above running results, we can see that , function fmod() The result of the remainder of is the same as the dividend , So it should be related to MATLAB The function in rem() The operation of is the same .
About this operation , The blogger has not found any related functions , It seems that only each element and each element can be left alone for the remainder operation .
Or you can subtract the true division result of the matrix operation from the result of rounding down .
Python There are two kinds of division and remainder operations in , One is to use the operator % Realization , The other is to use built-in functions divmod() Realization , Here are some examples .
The first one is : Use operators % Realization
# The case where both the dividend and the divisor are positive
a1 = 13
b1 = 5
c1 = a1 % b1
# The case where both the dividend and the divisor are negative
a2 = -14
b2 = -5
c2 = a2 % b2
# The divisor is a positive number , When the divisor is negative
a3 = 14
b3 = -5
c3 = a3 % b3
# The dividend is negative , The divisor is a positive number
a4 = -14
b4 = 5
c4 = a4 % b4
# Verify that the dividend is positive , When the divisor is negative , Whether the result is -1
a5 = 23
b5 = -6
c5 = a5 % b5
# Verify that the dividend is negative , When the divisor is positive , Whether the result is +1
a6 = -23
b6 = 6
c6 = a6 % b6
# Verify that the dividend is positive , When the divisor is negative and divisible , Whether the result is 0
a7 = -24
b7 = 6
c7 = a7 % b7
# Verify that the dividend is negative , When divisor is positive and divisible , Whether the result is 0
a8 = -24
b8 = 6
c8 = a8 % b8
The result is as follows :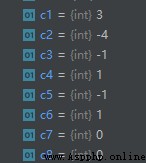
From the above calculation results, we can see :
that , We can conclude that , In fact, the sign of the remainder is the same as that of the divisor .
The second kind : With built-in functions divmod() Realization
function divmod() The grammar is as follows :
divmod(a, b)
If parameters a And Parameters b Are integers. , The result returned by the function is equivalent to (a // b, a % b).
If one of the parameters is a floating point number , The result returned by the function is equivalent to (q, a % b),q Usually math.floor(a / b), Function will make q * b + a % b May be close to a.
The remainder has the same sign as the divisor .
Be careful : When the divisor and the divisor are integers with different signs , The remainder has only three values , When divisible , Remainder is 0; When it's not divisible , If divisor is negative , Remainder is -1, If divisor is positive , Remainder is 1.
The sample code is as follows :
# The case where both the dividend and the divisor are positive
a1 = 13
b1 = 5
c01 = divmod(a1, b1)
# The case where both the dividend and the divisor are negative
a2 = -14
b2 = -5
c02 = divmod(a2, b2)
# The divisor is a positive number , When the divisor is negative
a3 = 14
b3 = -5
c03 = divmod(a3, b3)
# The dividend is negative , The divisor is a positive number
a4 = -14
b4 = 5
c04 = divmod(a4, b4)
# Verify that the dividend is positive , When the divisor is negative , Whether the result is -1
a5 = 23
b5 = -6
c05 = divmod(a5, b5)
# Verify that the dividend is negative , When the divisor is positive , Whether the result is +1
a6 = -23
b6 = 6
c06 = divmod(a6, b6)
# Verify that the dividend is positive , When the divisor is negative and divisible , Whether the result is 0
a7 = -24
b7 = 6
c07 = divmod(a7, b7)
# Verify that the dividend is negative , When divisor is positive and divisible , Whether the result is 0
a8 = -24
b8 = 6
c08 = divmod(a8, b8)
# The dividend is a positive floating-point number , The case where the divisor is a positive integer
a9 = 5.3
b9 = 2
c09 = divmod(a9, b9)
# The dividend is a negative floating-point number , The divisor is a negative integer
a10 = -5.3
b10 = -2
c10 = divmod(a10, b10)
# The dividend is a negative floating-point number , The case where the divisor is a positive integer
a11 = -5.3
b11 = 2
c11 = divmod(a11, b11)
# The dividend is a positive floating-point number , The divisor is a negative integer
a12 = 5.3
b12 = -2
c12 = divmod(a12, b12)
# The dividend is an integer , The divisor is a floating point number
a13 = 6
b13 = -2.2
c13 = divmod(a13, b13)
# The dividend is a floating point number , Divisor is also a floating point number
a14 = 6.8
b14 = -2.2
c14 = divmod(a14, b14)
The operation results are as follows :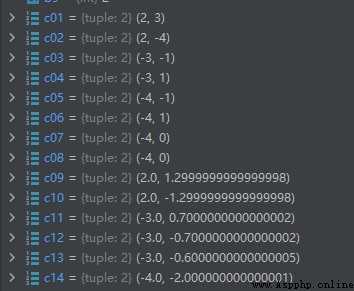
Numpy In the library ndarray There are three ways to remainder objects , See the blog for details https://blog.csdn.net/wenhao_ir/article/details/125226556 Of the 10 spot .
stay MATLAB You can use the function mod() and rem() Realize the remainder operation of division .
The grammar of the two is the same , The first parameter is the divisor , The second parameter is the divisor .
The grammar is as follows :
b = mod(a,m)
r = rem(a,b)
function mod() and rem() The difference between :
The main difference between them is that the expression of counting remainder is different :
function mod() The expression for calculating the remainder is : b = a - m.*floor(a./m), function floor() Is the rounding toward negative infinity , function floor() For details, please refer to the link :https://ww2.mathworks.cn/help/releases/R2019b/matlab/ref/floor.html
function rem() The expression for calculating the remainder is :r = a - b.*fix(a./b), function fix() Is the rounding towards the zero point of the coordinate axis , function fix() For details, please refer to the link :https://ww2.mathworks.cn/help/releases/R2019b/matlab/ref/fix.html
Such a result can be generated from the above formula :mod Function to produce a result that is zero or has the same sign as the divisor .rem Function to produce a result that is zero or has the same sign as the divisor . ask : Why is there such a result , You use the function floor() And the function fix() If you bring the definition of the concept into the actual example, you will understand .
Another difference is When the divisor is zero The agreement of .mod Function follows mod(a,0) return a The agreement of , and rem Function follows rem(a,0) return NaN The agreement of .
Both results have their own uses . for example , In signal processing ,mod Functions can be used in the context of periodic signals , Because its output is periodic ( Period equals divisor , and mod The sign of the remainder result of is the same as the divisor ).
The sample code is as follows :
a1 = mod(9,4);
a2 = rem(9,4);
b1 = mod(-9,4);
b2 = rem(-9,4);
c1 = mod(-9.3,4)
c2 = mod(-9.3,4)
The operation results are as follows :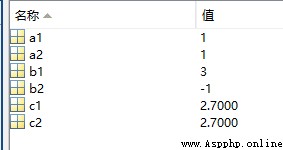
As can be seen from the above results , When the divisor is positive , The results of the two functions are the same , But when the divisor and the divisor sign are different , The results will show different results due to different rounding methods in the calculation process .
 Remember the experience of stepping on the pit of Python 3s console virtual terminal sequence (console color output, colorama / console library) under Windows
Remember the experience of stepping on the pit of Python 3s console virtual terminal sequence (console color output, colorama / console library) under Windows
前言My computer is configured to